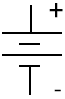Battery (electricity)
In science and technology, a battery is a device that stores chemical energy and makes it available in an electrical form. Batteries consist of electrochemical devices such as one or more galvanic cells, fuel cells or flow cells. Strictly, an electrical "battery" is an interconnected array of similar cells, but the term "battery" is also commonly applied to a single cell that is used on its own.
With technological progress, various types of batteries have been developed for use in diverse ways. Their applications range from portable electronic devices to automobiles and space probes.
History
The earliest known artifacts that may have been batteries are the so-called "Baghdad Batteries," apparently used in the period between 250 B.C.E. and 640 C.E. The term "battery" in this context was first used by Benjamin Franklin to describe a set of linked Leyden jars, the first capacitor and an early means of storing charge before the invention of true electrochemical batteries.
The modern development of batteries started with the Voltaic pile, invented by Italian physicist Alessandro Volta, who announced it in 1800.[1]. This battery consisted of a pile of zinc and copper discs separated by brine soaked cardboard.
A British chemist named John Frederic Daniell searched for a way to eliminate gas buildup in the Voltaic pile. His solution was to use a second electrolyte to consume the hydrogen produced by the first. In 1836, he invented the Daniell cell, which consisted of a copper pot filled with a copper sulfate solution, in which was immersed an unglazed earthenware container filled with sulfuric acid, in which was immersed a zinc electrode. Up to this point, all batteries were permanently drained when their chemical reactions were spent.
In 1859, Gaston Planté invented the lead/acid cell, the first battery that could be recharged by passing a reverse current through it. A lead/acid cell consists of a lead anode and a lead oxide cathode immersed in sulfuric acid. Both electrodes react with the acid to produce lead sulfate, but the reaction at the lead anode releases electrons whilst the reaction at the lead oxide consumes them, thus producing a current. These chemical reactions can be reversed by passing a reverse current through the battery, thereby recharging it. Planté's first model consisted of a sheet of lead and a sheet of lead oxide separated by rubber strips and rolled into a spiral.[2] His batteries were first used to power the lights in train carriages while stopped at a station.
In 1881, Camille Faure invented an improved version that consisted of a lead grid lattice into which a lead oxide paste was pressed, forming a plate. Multiple plates could be stacked for greater performance. This design was easier to mass-produce. Toward the end of the nineteenth century, Carl Gassner replaced the liquid electrolyte with a paste, making a much more practical battery for mass consumption.
In 1866, Georges Leclanché invented a battery that consisted of a zinc anode wrapped in a porous material and a manganese dioxide cathode, dipped in ammonium chloride. The manganese dioxide cathode had a little carbon mixed into it as well, which improved electrolyte conductivity and absorption.[3]
In 1887, Carl Gassner patented a variant of the Leclanché cell which came to be known as the dry cell because it did not have an free liquid electrolyte. Instead, the ammonium chloride was mixed with Plaster of Paris to create a paste, with a bit of zinc chloride added in to extend the shelf life. The manganese dioxide cathode was dipped in this paste, and both were sealed in a zinc shell which also acted as the anode.
Near the turn of the twentieth century, early gasoline-powered cars were unreliable and the electric car was more popular. However, their popularity was limited by the very heavy lead-acid batteries on which they ran. Hoping to produce a more commercially viable electric car, Thomas Edison and his associates began searching for a more lightweight and durable rechargeable battery. In 1903 their research produced a battery that consisted of iron and nickel electrodes with potassium hydroxide as the electrolyte (hence the "alkaline" descriptor, though this battery is more commonly referred to as the nickel-iron battery). However, consumers found this early version to be prone to leakage and short life; it did not outperform the lead-acid battery by much either. Edison went back to the drawing board and seven years later put out a more reliable and powerful model. By this time, however, the inexpensive and reliable Model T Ford had made gasoline engine cars the standard. Nevertheless, Edison's battery achieved great success in other applications.
The most common type of battery sold todayâthe alkaline batteryâwas developed in 1955 by the Eveready company.
Battery concepts
A battery is a device in which chemical energy is directly converted to electrical energy. It consists of one or more voltaic cells, each of which is composed of two half cells connected in series by the conductive electrolyte[4]. In the figure to the right, the battery consists of one or more voltaic cells in series. The conventional symbol does not necessarily represent the true number of voltaic cells. Each cell has a positive terminal, shown by a long horizontal line, and a negative terminal, shown by the shorter horizontal line. These do not touch each other but are immersed in a solid or liquid electrolyte.
The electrolyte is a conductor that connects the half-cells together. It also contains ions that can react with chemicals of the electrodes. Chemical energy is converted into electrical energy by chemical reactions that transfer charge between the electrode and the electrolyte at their interface. Such reactions are called faradaic, and are responsible for current flow through the cell. Ordinary, non-charge-transferring (non-faradaic) reactions also occur at the electrode-electrolyte interfaces. Non-faradaic reactions are one reason that voltaic cells (particularly the lead-acid cell of ordinary car batteries) "run down" when sitting unused.
Around 1800, Alessandro Volta studied the effect of different electrodes on the net electromotive force (emf) of many different types of voltaic cells. (Emf is equivalent to what was called the internal voltage source in the previous section.) He showed that the net emf (E) is the difference of the emfs Î1 and Î2 associated with the electrolyte-electrode interfaces within the two half-cells. Hence identical electrodes yield Î=0 (zero emf). Volta did not appreciate that the emf was due to chemical reactions. He thought that his cells were an inexhaustible source of energy, and that the associated chemical effects (e.g., corrosion) were a mere nuisance â rather than, as Michael Faraday showed around 1830, an unavoidable by-product of their operation.
Voltaic cells, and batteries of voltaic cells, are rated in volts, the SI unit of electromotive force. The voltage across the terminals of a battery is known as its terminal voltage. The terminal voltage of a battery that is neither charging nor discharging (the open-circuit voltage) equals its emf. The terminal voltage of a battery that is discharging is less than the emf, and that of a battery that is charging is greater than the emf.
Alkaline and carbon-zinc cells are rated at about 1.5 volts each, because of the nature of the chemical reactions in them. By comparison, given the high electrochemical potentials of lithium compounds, lithium cells can provide as much as 3 or more volts each. However, lithium compounds can be hazardous.
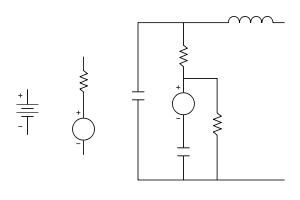
The conventional model for a voltaic cell, as drawn above, has the internal resistance drawn outside the cell. This is a correct Thevenin equivalent for circuit applications, but it oversimplifies the chemistry and physics. In a more accurate (and more complex) model, a voltaic cell can be thought of as two electrical pumps, one at each terminal (the faradaic reactions at the corresponding electrode-electrolyte interfaces), separated by an internal resistance largely due to the electrolyte. Even this is an oversimplification, since it cannot explain why the behavior of a voltaic cell depends strongly on its rate of discharge. For example, it is well known that a cell that is discharged rapidly (but incompletely) will recover spontaneously after a waiting time, but a cell that is discharged slowly (but completely) will not recover spontaneously.
The simplest characterization of a battery would give its emf (voltage), its internal resistance, and its capacity. In principle, the energy stored by a battery equals the product of its emf and its capacity.
Battery capacity
Given that the voltage of a battery is relatively constant, the capacity of a battery to store energy is often expressed in terms of the total amount of charge able to pass through the device. This is expressed in ampere hours, where one A·h equals 3600 coulombs. If a battery can pump charges for one hour at a rate of one coulomb/sec or one ampere (1 A), it has a capacity of 1 A·h. If it can provide 1 A for 100 hours, its capacity is 100 A·h. The more electrolyte and electrode material in the cell, the greater the capacity of the cell. Thus a tiny cell has much less capacity than a much larger cell, even if both rely on the same chemical reactions (e.g. alkaline cells), which produce the same terminal voltage. Because of the chemical reactions within the cells, the capacity of a battery depends on the discharge conditions such as the magnitude of the current, the duration of the current, the allowable terminal voltage of the battery, temperature, and other factors.
Battery manufacturers use a standard method to determine how to rate their batteries. The battery is discharged at a constant rate of current over a fixed period of time, such as 10 hours or 20 hours, down to a set terminal voltage per cell. So a 100Â ampere-hour battery is rated to provide 5Â A for 20Â hours at room temperature. The efficiency of a battery is different at different discharge rates. When discharging at low rate, the battery's energy is delivered more efficiently than at higher discharge rates. This is known as Peukert's Law.
Battery lifetime
Even if never taken out of the original package, disposable (or "primary") batteries can lose two to twenty-five percent of their original charge every year. This rate depends significantly on temperature, since typically chemical reactions proceed more rapidly as the temperature is raised. This is known as the "self discharge" rate and is due to non-faradaic (non-current-producing) chemical reactions, which occur within the cell even if no load is applied to it. Batteries should be stored at cool or low temperatures to reduce the rate of the side reactions. For instance, some people make a practice of storing unused batteries in their refrigerators to extend battery lifetime, although care should be taken to ensure the batteries do not freeze. Extremely high or low temperatures will reduce battery performance.
Rechargeable batteries self-discharge more rapidly than disposable alkaline batteries; up to three percent a day (depending on temperature). Due to their poor shelf life, they shouldn't be left in a drawer and then relied upon to power a flashlight or a small radio in an emergency. For this reason, it is a good idea to keep a few alkaline batteries on hand. Ni-Cd Batteries are almost always "dead" when you get them, and must be charged before first use.
Most NiMH and NiCd batteries can be charged several hundred times. Also, they both can be completely discharged and then recharged without their capacity being damaged or shortened. Automotive lead-acid rechargeable batteries have a much harder life. Because of vibration, shock, heat, cold, and sulfation of their lead plates, few automotive batteries last beyond six years of regular use. Automotive starting batteries have many thin plates to provide as many amps as possible in a reasonably small package, and are only drained a small amount before being immediately recharged. Care should be taken to avoid deep discharging a starter battery, as the recharging process melts a small amount of the lead from the plates. When holes form in the plates it results in less surface area for the chemical reaction, which results in less measured voltage. Leaving a lead-acid battery in a deeply discharged state for any length of time allows the sulfate to become more deeply adhered to the plate, making sulfate removal during the charging process difficult. This can result in less available plate surface and the resulting lower voltage, shortening the battery's life. "Deep-Cycle" lead-acid batteries such as those used in electric golf carts have much thicker plates to aid their longevity. The main benefit of lead-acid is its low cost, the main drawbacks are their large size and weight per a given capacity and voltage. Lead-acid batteries should never be discharged to below 20% of their full capacity as internal resistance will cause heat and damage when attempting to recharge them. Deep-cycle lead-acid systems often use a low-charge warning light or a low-charge power cut-off switch to prevent the type of damage that will shorten the battery's life.
Special "reserve" batteries intended for long storage in emergency equipment or munitions keep the electrolyte of the battery separate from the plates until the battery is activated, allowing the cells to be filled with the electrolyte. Shelf times for such batteries can be years or decades. However, their construction is more expensive than more common forms.
Battery explosion
A battery explosion is caused by the misuse or malfunction of a battery, such as attempting to recharge a primary battery, or short circuiting a battery. With car batteries, explosions are most likely to occur when a short circuit generates very large currents. In addition, car batteries liberate hydrogen when they are overcharged (because of electrolysis of the water in the electrolyte). Normally the amount of overcharging is very small, as is the amount of explosive gas developed, and the gas dissipates quickly. However, when "jumping" a car battery, the high current can cause the rapid release of large volumes of hydrogen, which can be ignited by a nearby spark (for example, when removing the jumper cables).
When a battery is recharged at an excessive rate, an explosive gas mixture of hydrogen and oxygen may be produced faster than it can escape from within the walls of the battery, leading to pressure build-up and the possibility of the battery case bursting. In extreme cases, the battery acid may spray violently from the casing of the battery and cause injury.
Additionally, disposing of a battery in fire may cause an explosion as steam builds up within the sealed case of the battery.
Overchargingâthat is, attempting to charge a battery beyond its electrical capacityâcan also lead to a battery explosion, leakage, or irreversible damage to the battery. It may also cause damage to the charger or device in which the overcharged battery is later used.
Types of batteries
From a user's viewpoint, at least, batteries can be generally divided into two main typesârechargeable and non-rechargeable (disposable). Each is in wide usage.
Disposable batteries, also called primary cells, are intended to be used once and discarded. These are most commonly used in portable devices with either low current drain, only used intermittently, or used well away from an alternative power source. Primary cells were also commonly used for alarm and communication circuits where other electric power was only intermittently available. Primary cells cannot be reliably recharged, since the chemical reactions are not easily reversible. Battery manufacturers recommend against attempting to recharge primary cells, although some electronics enthusiasts claim it is possible to do so using a special type of charger.
By contrast, rechargeable batteries, or secondary cells, can be re-charged after they have been drained. This is done by applying externally supplied electrical current, which reverses the chemical reactions that occur in use. Devices to supply the appropriate current are called chargers or rechargers.
The oldest form of rechargeable battery still in modern usage is the "wet cell" lead-acid battery. This battery is notable in that it contains a liquid in an unsealed container, requiring that the battery be kept upright and the area be well-ventilated to ensure safe dispersal of the hydrogen gas which is vented by these batteries during overcharging. The lead-acid battery is also very heavy for the amount of electrical energy it can supply. Despite this, its low manufacturing cost and its high surge current levels make its use common where a large capacity (over approximately 10Ah) is required or where the weight and ease of handling are not concerns.
A common form of lead-acid battery is the modern wet-cell car battery. This can deliver about 10,000 watts of power for a short period, and has a peak current output that varies from 450 to 1100 amperes. An improved type of lead-acid battery, called a gel battery (or "gel cell"), has become popular in automotive industry as a replacement for the lead-acid wet cell. The gel battery contains a semi-solid electrolyte to prevent spillage, electrolyte evaporation, and out-gassing, as well as greatly improving its resistance to damage from vibration and heat. Another type of battery, the Absorbed Glass Mat (AGM) suspends the electrolyte in a special fiberglass matting to achieve similar results. More portable rechargeable batteries include several "dry cell" types, which are sealed units and are therefore useful in appliances like mobile phones and laptops. Cells of this type (in order of increasing power density and cost) include nickel-cadmium (NiCd), nickel metal hydride (NiMH), and lithium-ion (Li-Ion) cells.
Disposable
Not designed to be rechargeableâsometimes called "primary cells."
- Zinc-carbon batteryâmid costâused in light drain applications.
- Zinc-chloride batteryâsimilar to zinc carbon but slightly longer life.
- Alkaline batteryâalkaline/manganese "long life" batteries widely used in both light drain and heavy drain applications.
- Silver-oxide batteryâcommonly used in hearing aids.
- Lithium batteryâcommonly used in digital cameras. Sometimes used in watches and computer clocks. Very long life (up to ten years in wristwatches) and capable of delivering high currents, but expensive.
- Mercury batteryâcommonly used in digital watches.
- Zinc-air batteryâcommonly used in hearing aids.
- Thermal batteryâhigh temperature reserve. Almost exclusively military applications.
- Water-activated batteryâused for radiosondes and emergency applications.
Rechargeable
Also known as secondary batteries or accumulators.
- Lead-acid batteryâcommonly used in vehicles, alarm systems and uninterruptible power supplies. Used to be used as an "A" or "wet" battery in valve/vacuum tube radio sets. The major advantage of this chemistry is its low costâa large battery (e.g. 70Ah) is relatively cheap when compared to other chemistries. However, this battery chemistry has lower energy density than other battery chemistries available today (see below)
- Absorbed glass mat is a class of lead-acid battery in which the electrolyte is absorbed into a fiberglass mat.
- Gel battery is a rechargeable valve regulated lead-acid battery with a gelified electrolyte.
- Lithium ion batteryâa relatively modern battery chemistry that offers a very high charge density (i.e. a light battery will store a lot of energy) and which does not suffer from any "memory" effect whatsoever. Used in laptops (notebook PCs), modern camera phones, some rechargeable MP3 players and most other portable rechargeable digital equipment.
- Lithium ion polymer batteryâsimilar characteristics to lithium-ion, but with slightly less charge density. This battery chemistry can be used for any battery to suit the manufacturer's needs, such as ultra-thin (1mm thick) cells for the latest PDAs.
- Nickel-cadmium batteryâused in many domestic applications but being superseded by Li-Ion and Ni-MH types. This chemistry gives the longest cycle life (over 1500 cycles), but has low energy density compared to some of the other chemistries. Ni-Cd cells using older technology suffer from memory effect, but this has been reduced drastically in modern batteries.
- NaS batteryâ(sodium-sulfur battery) is a type of battery constructed from sodium (Na) and sulfur (S). This type of battery exhibits a high energy density, high efficiency of charge/discharge (89â92%), long cycle life, and is made from inexpensive, non-toxic materials.
- Nickel-iron batteryâis a storage battery having a Nickel(III) oxide-hydroxide cathode and an iron anode, with an electrolyte of potassium hydroxide.
- Nickel metal hydride battery abbreviated NiMH, is a type of rechargeable battery similar to a nickel-cadmium (NiCd) battery but has a hydrogen-absorbing alloy for the anode instead of cadmium.
- Sodium-metal chloride battery, a new class of rechargeable sodium/beta-alumina battery in which the traditional liquid sulfur cathode is replaced by a chlorinated iron or nickel cathode, in the form of a porous metal matrix impregnated with molten sodium aluminum chloride.
- Nickel-zinc batteryâ(sometimes abbreviated NiZn) is a type of rechargeable battery commonly used in the light electric vehicle sector.
- Molten salt batteryâis a class of primary cell and secondary cell high temperature electric battery that uses molten salts as an electrolyte.
Homemade cells
Almost any liquid or moist object that has enough ions to be electrically conductive can serve as the electrolyte for a cell. As a novelty or science demonstration, it is possible to insert two electrodes made of different metals into a lemon, potato, glass of soft drink, etc. and generate small amounts of electricity. As of 2005, "two-potato clocks" are widely available in hobby and toy stores; they consist of a pair of cells, each consisting of a potato (lemon, etc.) with two electrodes inserted into it, wired in series to form a battery with enough voltage to power a digital clock. Homemade cells of this kind are of no real practical use, because they produce far less currentâand cost far more per unit of energy generatedâthan commercial cells, due to the need for frequent replacement of the fruit or vegetable. In addition, in the two-book series "Sneaky Uses for Everyday Things," there are instructions to make a battery from a nickel, a penny, and a piece of paper towel dipped in salt water. Each of these can make up to 0.3 volts and when many of them are used, they can replace normal batteries for a short amount of time
Lead acid cells can easily be manufactured at home, but a tedious charge/discharge cycle is needed to 'form' the plates. This is a process whereby lead sulfate forms on the plates, and during charge is converted to lead dioxide (positive plate) and pure lead (negative plate). Repeating this process results in a microscopically rough surface, with far greater surface area being exposed. This increases the current the cell can deliver.
Traction batteries
Traction batteries (secondary batteries or accumulators) are designed to provide power to move a vehicle, such as an electric car or tow motor. A major design consideration is power to weight ratio since the vehicle must carry the battery. While conventional lead acid batteries with liquid electrolyte have been used, the electrolyte in traction batteries is often gelled to prevent spilling. The electrolyte may also be embedded in a glass wool which is wound so that the cells have a round cross-sectional area (AGM-type).
Battery types used in electric vehicles
- Conventional lead-acid battery with liquid electrolyte.
- AGM-type (Absorbed Glass Mat)
- Zebra Na/NiCl2 battery operating at 270 °C requiring cooling in case of temperature excursions.
- NiZn battery (higher cell voltage 1.6 V and thus 25% increased specific energy, very short lifespan).
Lithium-ion batteries are now pushing out NiMh-technology in the sector while for low investment costs the lead-acid technology remains in the leading role[5].
Flow batteries
Flow batteries are a special class of battery where additional quantities of electrolyte are stored outside the main power cell of the battery, and circulated through it by pumps or by movement. Flow batteries can have extremely large capacities and are used in marine applications as well as gaining popularity in grid energy storage applications.
Zinc-bromine and vanadium redox batteries are typical examples of commercially-available flow batteries.
Maintenance-free (MF) battery
The MF (Maintenance Free) battery is one of many types of lead-acid battery. It became popular on motorcycles because its acid is absorbed into the medium which separates the plates, so it cannot spill, and this medium also lends support to the plates which helps them better to withstand vibration.
The electrical characteristics of MF batteries differ somewhat from wet-cell lead-acid batteries, and caution should be exercised in charging and discharging them. MF batteries should not be confused with AGM (Absorbed Glass Mat) batteries, which also have an absorbed electrolyte but again have different electrical characteristics.
Environmental considerations
Since their development over 250 years ago, batteries have remained among the most expensive energy sources, and their manufacture consumes many valuable resources and often involves hazardous chemicals. For this reason many areas now have battery recycling services available to recover some of the more toxic (and sometimes valuable) materials from used batteries. Batteries may be harmful or fatal if swallowed.
Electrical component
The cells in a battery can be connected in parallel, series, or in both. A parallel combination of cells has the same voltage as a single cell, but can supply a higher current (the sum of the currents from all the cells). A series combination has the same current rating as a single cell but its voltage is the sum of the voltages of all the cells. Most practical electrochemical batteries, such as 9 volt flashlight batteries and 12 V automobile (car) batteries, have several cells connected in series inside the casing. Parallel arrangements suffer from the problem that, if one cell discharges faster than its neighbor, current will flow from the full cell to the empty cell, wasting power and possibly causing overheating. Even worse, if one cell becomes short-circuited due to an internal fault, its neighbor will be forced to discharge its maximum current into the faulty cell, leading to overheating and possibly explosion. Cells in parallel are therefore usually fitted with an electronic circuit to protect them against these problems. In both series and parallel types, the energy stored in the battery is equal to the sum of the energies stored in all the cells.
A battery can be simply modeled as a perfect voltage source (i.e. one with zero internal resistance) in series with a resistor. The voltage source depends mainly on the chemistry of the battery, not on whether it is empty or full. When a battery runs down, its internal resistance increases. When the battery is connected to a load (e.g. a light bulb), which has its own resistance, the resulting voltage across the load depends on the ratio of the battery's internal resistance to the resistance of the load. When the battery is fresh, its internal resistance is low, so the voltage across the load is almost equal to that of the battery's internal voltage source. As the battery runs down and its internal resistance increases, the voltage drops across its internal resistance increases, so the voltage at its terminals decreases, and the battery's ability to deliver power to the load decreases.
See also
Notes
- â "On the Electricity excited by the mere Contact of conducting Substances of different Kinds. In a Letter from Mr. Alexandro Volta, F.R.S., Professor of Natural Philosophy at the University of Pavia, to the Rt. Hon. Sir. Joseph Banks, Bart. K.B. P.R.S. Read June 26, 1800.". Philosophical Transactions of the Royal Society of London (1800):403-431. Retrieved December 27, 2017.
- â Corrosion-doctors.org Gaston PlantĂ© (1834-1889) Retrieved December 27, 2017.
- â Molecular Expressions Zinc-Carbon Batteries Retrieved December 27, 2017.
- â Anne Marie Helmenstine, Half-Cell Definition ThoughtCo., 2017. Retrieved December 27, 2017.
- â Matheys, J. and W. Van Autenboer. Subat: Sustainable Batteries. Retrieved December 27, 2017.
ReferencesISBN links support NWE through referral fees
- Linden, David; Reddy, Thomas B. Handbook Of Batteries. New York, NY: McGraw-Hill Professional, 2001. ISBN 0071359788
- Dell, R.M., and D. Rand. Understanding Batteries. London, England: Royal Society of Chemistry, 2001. ISBN 0854046054
- Buchmann, Isidor. Batteries in a Portable World: A Handbook on Rechargeable Batteries for Non-Engineers. Richmond, BC, Canada: Cadex Electronics, 2001. ISBN 0968211828
External links
All links retrieved September 20, 2023.
- Bellis, Mary. History Timeline of the Battery ThoughtCo, 2017.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.