Logical connective

In logic, two sentences (either in a formal language or a natural language) may be joined by means of a logical connective to form a compound sentence. The truth-value of the compound is uniquely determined by the truth-values of the simpler sentences. The logical connective therefore represents a function, and since the value of the compound sentence is a truth-value, it is called a truth-function and the logical connective is called a "truth-functional connective." The truth-functions include conjunction ("and"), disjunction ("or"), and implication ("if … then").

Mathematical logic is a mathematical representation of formal rules of human thought, which philosophers have been attempting to develop since Aristotle. Philosophical arguments are often incomprehensible due to obscure or ambiguous expressions. Logical connectives are basic units which constitute the logical structure of an argument. By applying these conceptual tools, arguments can become clearer, communicable, and comprehensible.

Truth functions in natural languages

In the grammar of natural languages two sentences may be joined by a grammatical conjunction to form a grammatically compound sentence. Some but not all such grammatical conjunctions are truth-functions. For example consider the following sentences:

A: Jack went up the hill.

B: Jill went up the hill.

C: Jack went up the hill and Jill went up the hill.

D: Jack went up the hill so Jill went up the hill.

The words and and so are both grammatical conjunctions joining the sentences (A) and (B) to form the compound sentences (C) and (D). The and in (C) is a logical connective, since the truth of (C) is completely determined by (A) and (B): it would make no sense to affirm (A) and (B) but deny (C). However so in (D) is NOT a logical connective, since it would be quite reasonable to affirm (A) and (B) but deny (D): Perhaps, after all, Jill went up the hill fetch a pail of water, not because Jack had gone up the Hill at all. Thus, and is a logical connective but so is not. In the realm of pure logic, (C) is a compound statement but (D) is not. (D) cannot be broken into parts using only the logic of statements, the realm of cause and effect being proper to science rather than logic.

Various English words and word pairs express truth-functions, and some of them are synonymous. Examples (with the name of the relationship in parentheses) are:

"and" (conjunction), "or" (inclusive or exclusive disjunction), "implies" (implication), "if … then" (implication), "if and only if" (equivalence), "only if" (implication), "just in case" (equivalence), "but" (conjunction), "however" (conjunction) , "not both" (NAND), "neither … nor" (NOR). The word "not" (negation) and "it is false that" (negation) "it is not the case that" (negation) are also English words expressing a logical connective, even though they are applied to a single statement, and do not connect two statements.

Truth functions in formal languages

In formal languages truth-functions are represented by unambiguous symbols, and these can be exactly defined by means of truth tables. There are 16 binary truth tables, and so 16 different logical connectives which connect exactly two statements, can be defined. Not all of them are in common use. These symbols are called "truth-functional connectives," "logical connectives," "logical operators," or "propositional operators."

Logical connectives can be used to link more than two statements. A more technical definition is that an "n-ary logical connective" is a function which assigns truth values "true" or "false" to n-tuples of truth values.

Introduction

The basic logical operators are: Negation (not) (¬ or ~) Conjunction (and) ($\wedge$ or &) Disjunction (or) ($\vee$) Material implication (if...then) ($\rightarrow$, $\Rightarrow$ or $\supset$) Biconditional (if and only if) (xnor) ($\leftrightarrow$, $\equiv$, or $=$)

Some others are: Exclusive disjunction (xor) ($\not \leftrightarrow$) Joint denial (nor) (↓) Alternative denial (nand) (↑) Material nonimplication ($\not \rightarrow$) Converse nonimplication ($\not \leftarrow$) Converse implication ($\leftarrow$) Tautology ($\top$) Contradiction ($\bot$)

For example, the statements it is raining and I am indoors can be reformed using various different connectives to form sentences that relate the two in ways which augment their meaning:

• It is raining and I am indoors.
• If it is raining then I am indoors.
• It is raining if I am indoors.
• It is raining if and only if I am indoors.
• It is not raining.

If one writes "P" for It is raining and "Q" for I am indoors, and uses the usual symbols for logical connectives, then the above examples could be represented in symbols, respectively:

• P & Q
• P $\to$ Q
• Q $\to$ P
• P $\leftrightarrow$ Q
• ¬P

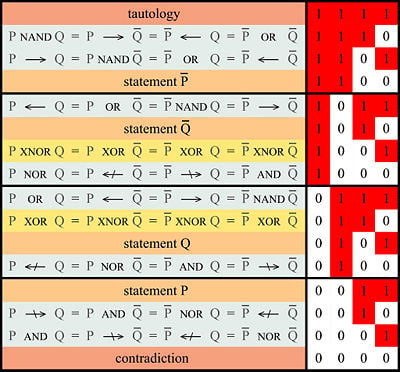
All binary logical connectives

There are sixteen different Boolean functions, associating the inputs P and Q with four digit binary outputs.

The following table shows important equivalences like the De Morgan's laws (lines 1000 and 1110) or the law of Contraposition (line 1101).

Table of all logical connectives

Functional completeness

Not all of these operators are necessary for a functionally complete logical calculus. Certain compound statements are logically equivalent. For example, ¬P ∨ Q is logically equivalent to P → Q So the conditional operator "→" is not necessary if you have "¬" (not) and "∨" (or)

The smallest set of operators which still expresses every statement which is expressible in the propositional calculus is called a minimal functionally complete set. A minimally complete set of operators is achieved by NAND alone { ↓ } and NOR alone { ↑ }.

The following are the functionally complete sets (of cardinality not exceeding 2) of operators whose arities do not exceed 2:

{ ↓ }, { ↑ }, { $\rightarrow$, $\neg$ }, { $\rightarrow$, $\not \leftrightarrow$ }, { $\neg$, ⊂ }, { $\rightarrow$, ⊄ }, { $\vee$, $\neg$ }, { $\rightarrow$, ⊅ }, { ⊄, $\neg$ }, { ⊂, $\not \leftrightarrow$ }, { ⊅, $\neg$ }, { ⊂, ⊄ }, { $\wedge$, $\neg$ }, { ⊂, ⊅ }, { $\bot$, $\rightarrow$ }, { ⊄, $\leftrightarrow$ }, { ⊅, $\leftrightarrow$ }

Properties

The logical connectives each possess different set of properties which may be expressed in the theorems containing the connective. Some of those properties that a logical connective may have are:

• Associativity: Within an expression containing two or more of the same associative operators in a row, the order of the operations does not matter as long as the sequence of the operands is not changed. For example:

(x • y) • z = x • (y • z)

• Commutivity: Each pair of variables connected by the operator may be exchanged for each other without affecting the truth-value of the expression. For example:

x • y = y • x

• Distributivity: Given a set S and two binary operations • and + on S, one says that the operation •

is left-distributive over + if, given any elements x, y, and z of S,

x • (y + z) = (x • y) + (x • z);

is right-distributive over + if, given any elements x, y, and z of S:

(y + z) • x = (y • x) + (z • x);

is distributive over + if it is both left- and right-distributive.

• Idempotency: Multiple applications of the operation does not change the result. For example:

1 x 1 = 1

• Absorption: An identity linking a pair of binary operations. For example, any two binary operations, say $ and %, are subject to the absorption law if:

a $ (a % b) = a % (a $ b) = a.

The operations $ and % are said to form a dual pair.

A set of operators is functionally complete if and only if for each of the following five properties it contains at least one member lacking it:

• monotonic: If f(a₁, ..., a_n) ≤ f(b₁, ..., b_n) for all a₁, ..., a_n, b₁, ..., b_n ∈ {0,1} such that a₁ ≤ b₁, a₂ ≤ b₂, ..., a_n ≤ b_n. E.g., $\vee$, $\wedge$, $\top$, $\bot$.
• affine: Each variable always makes a difference in the truth-value of the operation or it never makes a difference. E.g., $\neg$, $\leftrightarrow$, $\not \leftrightarrow$, $\top$, $\bot$.
• Self dual: To read the truth-value assignments for the operation from top to bottom on its truth table is the same as taking the complement of reading it from bottom to top, in other words f(¬a₁, ..., ¬a_n) = ¬f(a₁, ..., a_n). For example, $\neg$.
• Truth-preserving: The interpretation under which all variables are assigned a truth value of 'true' produces a truth value of 'true' as a result of these operations. E.g., $\vee$, $\wedge$, $\top$, $\rightarrow$, $\leftrightarrow$, ⊂.
• Falsehood-preserving: The interpretation under which all variables are assigned a truth value of "false" produces a truth value of 'false' as a result of these operations. For example, $\vee$, $\wedge$, $\not \leftrightarrow$, $\bot$, ⊄, ⊅.

Arity

In two-valued logic there are 2 nullary operators (constants), 4 unary operators, 16 binary operators, 256 ternary operators, and $2^{2^{n}}$ n-ary operators. In three valued logic there are 3 nullary operators (constants), 27 unary operators, 19683 binary operators, 7625597484987 ternary operators, and $3^{3^{n}}$ n-ary operators. An n-ary operator in k-valued logic is a function from $\mathbb {Z} _{k}^{n}\to \mathbb {Z} _{k}$. Therefore, the number of such operators is $|\mathbb {Z} _{k}|^{|\mathbb {Z} _{k}^{n}|}=k^{k^{n}}$, which is how the above numbers were derived.

However, some of the operators of a particular arity are actually degenerate forms that perform a lower-arity operation on some of the inputs and ignores the rest of the inputs. Out of the 256 ternary boolean operators cited above, ${\binom {3}{2}}\cdot 16-{\binom {3}{1}}\cdot 4+{\binom {3}{0}}\cdot 2$ of them are such degenerate forms of binary or lower-arity operators, using the inclusion-exclusion principle. The ternary operator $f(x,y,z)=\lnot x$ is one such operator which is actually a unary operator applied to one input, and ignoring the other two inputs.

"Not" is a unary operator, it takes a single term (¬P). The rest are binary operators, taking two terms to make a compound statement (P $\wedge$ Q, P, $\vee$ Q, P → Q, P ↔ Q).

The set of logical operators $\Omega \!$ may be partitioned into disjoint subsets as follows:

$\Omega =\Omega _{0}\cup \Omega _{1}\cup \ldots \cup \Omega _{j}\cup \ldots \cup \Omega _{m}\,.$

In this partition, $\Omega _{j}\!$ is the set of operator symbols of arity $j\!$.

In the more familiar propositional calculi, $\Omega \!$ is typically partitioned as follows:

nullary operators: $\Omega _{0}=\{\bot ,\top \}\,$

unary operators: $\Omega _{1}=\{\lnot \}\,$

binary operators: $\Omega _{2}\subseteq \{\land ,\lor ,\rightarrow ,\leftrightarrow \}\,$

Order of precedence

As a way of reducing the number of necessary parentheses, one may introduce precedence rules: ¬ has higher precedence than ∧, ∧ higher than ∨, and ∧ higher than →. So for example, P ∨ Q ∧ ¬R → S is short for (P ∨ (Q ∧ (¬R))) → S.

Here is a table that shows a commonly used precedence of logical operators.

Operator	Precedence
¬	1
∧	2
∨	3
→	4
$\leftrightarrow$	5

The order of precedence determines which connective is the "main connective" when interpreting a non-atomic formula.

Applications in computer science

Logical operators are implemented as logic gates in digital circuits. Practically all digital circuits (the major exception is DRAM) are built up from NAND, NOR, NOT, and transmission gates. NAND and NOR gates with 3 or more inputs rather than the usual 2 inputs are fairly common, although they are logically equivalent to a cascade of 2-input gates. All other operators are implemented by breaking them down into a logically equivalent combination of 2 or more of the above logic gates.

The "logical equivalence" of "NAND alone," "NOR alone," and "NOT and AND" is similar to Turing equivalence.

Is some new technology (such as reversible computing, clockless logic, or quantum dots computing) "functionally complete," in that it can be used to build computers that can do all the sorts of computation that CMOS-based computers can do? If it can implement the NAND operator, only then is it functionally complete.

That fact that all logical connectives can be expressed with NOR alone is demonstrated by the Apollo guidance computer.

In logic, a set of symbols is commonly used to express logical representation. As logicians are familiar with these symbols, they are not explained each time they are used. So, for students of logic, the following table lists many common symbols together with their name, pronunciation and related field of mathematics. Additionally, the third column contains an informal definition, and the fourth column gives a short example.

Be aware that, outside of logic, different symbols have the same meaning, and the same symbol has, depending on the context, different meanings.

Basic logic symbols

Symbol	Name	Explanation	Examples	Unicode Value	HTML Entity	LaTeX symbol
	Should be read as
	Category
⇒ → ⊃	material implication	A ⇒ B means if A is true then B is also true; if A is false then nothing is said about B. → may mean the same as ⇒ (the symbol may also indicate the domain and codomain of a function; see table of mathematical symbols). ⊃ may mean the same as ⇒ (the symbol may also mean superset).	x = 2  ⇒  x2 = 4 is true, but x2 = 4   ⇒  x = 2 is in general false (since x could be −2).	8658 8594 8835	⇒ → ⊃	$\Rightarrow$\Rightarrow $\to$\to $\supset$\supset
	implies; if .. then
	propositional logic, Heyting algebra
⇔ ≡ ↔	material equivalence	A ⇔ B means A is true if B is true and A is false if B is false.	x + 5 = y +2  ⇔  x + 3 = y	8660 8801 8596	⇔ ≡ ↔	$\Leftrightarrow$\Leftrightarrow $\equiv$\equiv $\leftrightarrow$\leftrightarrow
	if and only if; iff
	propositional logic
¬ ˜	logical negation	The statement ¬A is true if and only if A is false. A slash placed through another operator is the same as "¬" placed in front.	¬(¬A) ⇔ A x ≠ y  ⇔  ¬(x =  y)	172 732	¬ ˜ ~	$\lnot$\lnot ${\tilde {}}$\tilde{}
	not
	propositional logic
∧ &	logical conjunction	The statement A ∧ B is true if A and B are both true; else it is false.	n < 4  ∧  n >2  ⇔  n = 3 when n is a natural number.	8743 38	&and; &	$\land$\land \&
	and
	propositional logic
∨	logical disjunction	The statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false.	n ≥ 4  ∨  n ≤ 2  ⇔ n ≠ 3 when n is a natural number.	8744	&or;	$\lor$\lor
	or
	propositional logic
⊕ ⊻	exclusive or	The statement A ⊕ B is true when either A or B, but not both, are true. A ⊻ B means the same.	(¬A) ⊕ A is always true, A ⊕ A is always false.	8853 8891	&oplus;	$\oplus$\oplus
	xor
	propositional logic, Boolean algebra
⊤ T 1	logical truth	The statement ⊤ is unconditionally true.	A ⇒ ⊤ is always true.	8868	T	$\top$\top
	top
	propositional logic, Boolean algebra
⊥ F 0	logical falsity	The statement ⊥ is unconditionally false.	⊥ ⇒ A is always true.	8869	&perp; F	$\bot$\bot
	bottom
	propositional logic, Boolean algebra
∀	universal quantification	∀ x: P(x) means P(x) is true for all x.	∀ n ∈ N: n2 ≥ n.	8704	&forall;	$\forall$\forall
	for all; for any; for each
	predicate logic
∃	existential quantification	∃ x: P(x) means there is at least one x such that P(x) is true.	∃ n ∈ N: n is even.	8707	&exist;	$\exists$\exists
	there exists
	first-order logic
∃!	uniqueness quantification	∃! x: P(x) means there is exactly one x such that P(x) is true.	∃! n ∈ N: n + 5 = 2n.	8707 33	&exist; !	$\exists !$\exists !
	there exists exactly one
	first-order logic
:= ≡ :⇔	definition	x := y or x ≡ y means x is defined to be another name for y (but note that ≡ can also mean other things, such as congruence). P :⇔ Q means P is defined to be logically equivalent to Q.	cosh x := (1/2)(exp x + exp (−x)) A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B)	58 61 8801 58 8660	:= : &equiv; &hArr;	$:=$:= $\equiv$\equiv $\Leftrightarrow$\Leftrightarrow
	is defined as
	everywhere
( )	precedence grouping	Perform the operations inside the parentheses first.	(8/4)/2 = 2/2 = 1, but 8/(4/2) = 8/2 = 4.	40 41	( )	$(~)$ ( )
	everywhere
⊢	inference	x ⊢ y means y is derived from x.	A → B ⊢ ¬B → ¬A	8866		$\vdash$\vdash
	infers or is derived from
	propositional logic, first-order logic

See also

• Formal logic
• Fuzzy logic
• History of logic
• logic
• Metalogic
• Modal logic
• Proof (logic)
• Propositional calculus

References

ISBN links support NWE through referral fees

• Church, Alonzo. Introduction to Mathematical Logic. Princeton mathematical series, 17. Princeton: Princeton University Press, 1956.
• Copi, Irving M. Symbolic Logic. New York: Macmillan, 1954.
• Enderton, Herbert. A Mathematical Introduction to Logic, 2nd ed. Boston, MA: Academic Press, 2001. ISBN 978-0-12-238452-3.
• Martin, Robert M. Introducing Symbolic Logic. Peterborough, ON: Broadview Press, 2004. ISBN 9781551116358.
• Ochieng'-Odhiambo, F. Introductory Symbolic Logic. Guide to philosophy series, no. 7 (rev. ed.). Nairobi: Consolata Institute of Philosophy, 2003. ISBN 9789966820068.
• Quine, W. V. Mathematical Logic. Cambridge: Harvard University Press, 1951.
• Rosenbloom, Paul C. The Elements of Mathematical Logic. The Dover series in mathematics and physics. New York: Dover Publications, 1950.
• Stoli︠a︡r, A. A. Introduction to Elementary Mathematical Logic. Cambridge, Mass: M.I.T. Press, 1970. ISBN 9780262190541.

External links

All links retrieved November 3, 2022.

• "Logical constants," Stanford Encyclopedia of Philosophy.
• Cullinane, Steven H. "The geometry of logic."
• Introduction to logic

General philosophy sources

• Stanford Encyclopedia of Philosophy
• Paideia Project Online
• The Internet Encyclopedia of Philosophy
• Project Gutenberg

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Logical_connective  ^history
• Table_of_logic_symbols  ^history
• Associativity  ^history
• Commutativity  ^history
• Distributivity  ^history
• Idempotence  ^history
• Absorption_law  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Logical connective"

Note: Some restrictions may apply to use of individual images which are separately licensed.