Paradox

For other uses, see Paradox (disambiguation).

Robert Boyle's self-flowing flask fills itself in this diagram, but perpetual motion machines cannot exist (according to our present understanding of physics).

A paradox was originally something that was contrary to received or common opinion. The term paradox comes from the Greek para ("contrary to") and doxa ("opinion"). From that, the term came to be used for something that was contrary to, or contradicted, common sense. Today the term is usually used for something that is an apparently true statement or group of statements that leads to a contradiction or a situation which defies intuition.

Sometimes either the statements in question do not really imply the contradiction and the puzzling result is not really a contradiction, or the premises themselves are not all really true, or cannot all be true together. The recognition of ambiguities, equivocations, and unstated assumptions underlying known paradoxes has sometimes led to significant advances in science, philosophy, and mathematics.

The word "paradox" is often used interchangeably and wrongly with "contradiction;" but where a contradiction by definition cannot be true, many paradoxes do allow for resolution, though many remain unresolved or only contentiously resolved, such as Curry's paradox. Still more casually, the term is sometimes used for situations that are merely surprising, albeit in a distinctly "logical" manner, such as the Birthday Paradox. This is also the usage in economics, where a paradox is an unintuitive outcome of economic theory.

The etymology of paradox can be traced back to at least Plato's Parmenides, where Zeno of Elea used the word "paradoxon" to describe some of his seminal philosophic ideas.

It is unknown if incarnations of paradox were used before Zeno of Elea. Later and more frequent usage of the word has been traced to the early Renaissance. Early forms of the word appeared in the late Latin paradoxum and the related Greek παράδοξος paradoxos, which means "contrary to expectation," or "incredible."

All that said, there are some genuine paradoxes, statements that, if true, are false, and if false, are true.

Zeno's Paradoxes

The first known paradoxes were given by the ancient Greek School of philosophy at Elea. Parmenides (c. 515-c.450 B.C.E.) had held that motion is an illusion and that existence is one indivisible whole. His student and follower Zeno (490-430 B.C.E.), regarded by Aristotle as being the founder of dialectic, produced a number of paradoxes that purport to demonstrate that space, time, and especially motion are inherently contradictory, and thus cannot exist; this result was in support of the positions of Parmenides. The Chinese philosopher Hui Shi independently put forward the same paradoxes at about the same time, and the Indian philosopher Nagarjuna took a similar approach somewhat later (Reese, p. 549).

The millet seed. If a single millet seed is dropped to the ground, it does not make a sound. A bushel of millet seeds is merely an aggregate of many millet seeds, but if it is poured out onto the ground it seems to make a sound. It is a paradox that 10,000 dropped seeds should make a sound when a single dropped seed does not, since any number of multiplications of no sound (nothing, or zero) should not produce anything other than no sound (nothing, or zero).

Falsity of the premise "There are many things." (a) "If there are many things, they must be both great and small; so small as to have no size, so great as to be infinite." The next part of the argument employs the principle of division: Anything that has size can be divided into two things, each with size, so the process has no termination. (b) If there is a plurality, the finite things must be both finite and infinite in number. It must be finite because a plurality requires a finite and definite number; infinite because two or more things require boundaries or distinguishing marks, but here again a progression toward infinity arises when those things are broken into smaller things. (c) "If there are many things, they must be both like and unlike." The argument for that claim is not given (From Hondereich, p. 922).

Divisibility of a line. A line is either divisible or indivisible. If divisible, it is divisible into either a finite or an infinite number of parts, each of which either has or lacks magnitude. If finite but lacking magnitude, then one cannot reconstruct the line because any number of parts of zero magnitude is still zero. If it is an infinite number of parts of zero magnitude, the same result is yielded (because an infinite multiplication of zero is still zero). But if the line is divisible into an infinite number of parts of any magnitude, then this would constitute a much longer line than the original (because an infinite multiplication of any magnitude greater than zero yields an infinite magnitude). Thus, lines are not divisible.

The arrow. The flying arrow cannot really be flying because if it is moving, it must either be moving in a place where it is, or in a place where it is not. But if it is in the place that it is (i.e. a place exactly equal to its length), then it is at rest, and if it is moving into a place where it is not, this cannot be because it cannot be where it is not.

The relativity of time and motion.

Achilles and the tortoise. If the tortoise starts the race somewhere in front of Achilles and they both start at the same time, then Achilles, in an effort to overtake the tortoise, must first cover the distance between his starting point and the starting point of the tortoise, but in that time the tortoise will have moved forward. So Achilles must then cover that distance. But the tortoise will have moved on, and Achilles must cover that, and so on, with an infinite iteration of this necessity. Thus Achilles cannot catch the tortoise so long as the tortoise remains in motion.

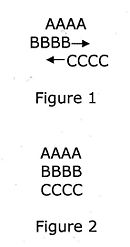
The relativity of time and motion. Suppose there are three rows of runners, each with the same number of individuals. One row (A) is at rest, and the other two rows (B and C) are moving in opposite directions, according to this pattern: (Figure 1)

They will then reach this position: (Figure 2)

But to move from the situation depicted in Figure 1 to that of Figure 2, B's will have passed twice as many Cs as As. Hence, it would take the Bs twice as long to pass the individual As as the individual Cs. So it seems that double the time is equal to half the time. (Reese, p. 852)

Zeno's paradoxes have fascinated and tormented philosophers, philosophy students, and others to this day because it is seems, intuitively, that there is a mistake in each, but figuring out what the mistake is may be difficult or even impossible, at least for some time. Since each of them, except possibly the one on the relativity of time and motion, really does have a mistake in it, they are only apparent paradoxes and not true ones. But it was not until certain mathematical developments of the nineteenth century that a definitive solution to some of them was found.

Some other paradoxes

The Megarian and Stoic philosophers discovered a number of paradoxes, called insolubilia. One such came from Epimenides, a Cretan, who declared that all Cretans are liars. This is usually known as the liar paradox. It can also be expressed, "The statement I am making to you right now is a lie."

P.E.B. Jourdain had a card that, on one side, said only "The sentence the other side of this card is false," and, on the other side, had only the sentence, "The sentence on the other side of this card is false."

Sometimes supernatural or science fiction themes are held to be impossible due to resultant paradoxial conditions. The theme of time travel has staged many popular paradoxes arising from the traveler interfering with the past. Suppose Jones, who was born in 1950, travels back in time to 1901 and kills his own grandfather. It follows that neither his father nor he himself will be born; but then he would not have existed to travel back in time and kill his own grandfather; but then his grandfather would not have died and Jones himself would have lived; etc. This is known as the Grandfather paradox.

Paradoxes that arise from apparently intelligible uses of language are often of interest to logicians and philosophers. "This sentence is false" is an example of the famous liar paradox: it is a sentence which cannot be consistently interpreted as true or false, because if it is false it must be true, and if it is true it must be false. Therefore, it can be concluded the sentence is both true and false.

Russell's paradox, also known as the Zermelo Paradox (after the German mathematician Ernst Zermelo, 1871-1953), shows that the notion of "the set of all those sets that do not contain themselves" leads to a contradiction. Solving this led to restrictions on the notion of membership in sets, and was instrumental in the development of modern logic and set theory.

There are other paradoxes in mathematics and set theory. One is The Burali-Forti Paradox, concerning the greatest ordinal number. Russell produced a paradox concerning the greatest cardinal number. There is the Richard paradox having to do with definable and undefinable real numbers. And there are others.

Nelson Goodman's problem of the predicates Grue and Bleen and their definability in terms of the predicates Blue and Green with a temporal marker, and vice versa, seems to be a paradox. Goodman and others also presented the Paradoxes of Confirmation, such as showing that the claim "All crows are black" seems to be confirmed by discovering non-black non-crows.

P.F. Strawson produced a purported solution to the liar paradox through his usage of the performative view of truth. Since saying that a sentence is true is the performative act of agreeing with the sentence, it is like saying "ditto." But if there is no original sentence to say "ditto" to, the paradox, Strawson claimed, disappears (Reese, p. 550).

Common themes

Common themes in paradoxes include direct and indirect self-reference, infinity, circular definitions, and confusion of levels of reasoning. Paradoxes which are not based on a hidden error generally happen at the fringes of context or language, and require extending the context or language to lose their paradox quality.

In moral philosophy, paradox plays a central role in ethics debates. For instance, it may be considered that an ethical admonition to "love thy neighbor" is not just in contrast with, but in contradiction to an armed neighbor actively trying to kill him: If he or she succeeds, he will not be able to love him or her. But to preemptively attack them or restrain them is not usually understood as loving. This might be termed an ethical dilemma. Another example is the conflict between an injunction not to steal and one to care for a family that the subject cannot afford to feed without stolen money.

Types of paradoxes

W. V. Quine (1962) distinguished between three classes of paradoxes.

A veridical paradox produces a result that appears absurd but is demonstrated to be true nevertheless. Thus, the paradox of Frederic's birthday in The Pirates of Penzance establishes the surprising fact that a person may be more than nine years old on his ninth birthday. Likewise, Arrow's impossibility theorem involves behavior of voting systems that is surprising but all too true.
A falsidical paradox establishes a result that not only appears false but actually is false; there is a fallacy in the supposed demonstration. The various invalid proofs (e.g. that 1 = 2) are classic examples, generally relying on a hidden division by zero. Another example would be the Horse paradox.
A paradox which is in neither class may be an antinomy, which reaches a self-contradictory result by properly applying accepted ways of reasoning. For example, the Grelling-Nelson paradox points out genuine problems in the understanding of the ideas of truth and description.

References
ISBN links support NWE through referral fees

Clarke, Michael. Paradoxes from A to Z. London: Routledge, 2002. ISBN 0415228085
Goodman, Nelson. Fact, Fiction, and Forecast, 3rd ed. Indianapolis: Bobbs-Merrill, 1973. ISBN 0672518899
Honderich, Ted, ed. The Oxford Companion to Philosophy. Oxford: Oxford University Press, 1995. ISBN 0198661320
Quine, W.V. "Paradox," Scientific American, April 1962, pp. 84–96.
Quine, W.V. The Ways of Paradox: And Other Essays. Cambridge: Harvard University Press, 1976. ISBN 0674948351
Reese, William L. Dictionary of Philosophy and Religion, New and Enlarged Edition. Atlantic Highlands, New Jersey: Humanities Press, 1996. ISBN 0391038648
Sainsbury, R. M., Paradoxes. Cambridge: Cambridge University Press, 1988. ISBN 052133165X

External links

All links retrieved November 18, 2022.

Entries on Paradox, Stanford Encyclopedia of Philosophy.
Definability paradoxes.
Mohammad Gani. Though Arrow Says It’s Impossible, It Happens Everyday.
Zeno and the Paradox of Motion, MathPages.

General Philosophy Sources

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

Paradox ^history

The history of this article since it was imported to New World Encyclopedia:

History of "Paradox"

Note: Some restrictions may apply to use of individual images which are separately licensed.