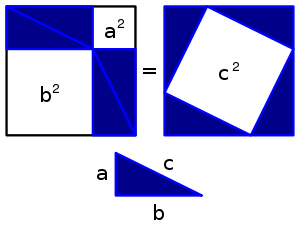
Theorem

A mathematical picture paints a thousand words: the Pythagorean theorem.

In logic, a theorem is formally meant to be a formula that can be transformed by applying inferential rules to axioms in a deductive system. This formal notion of proofs in logic is crucial in fields such as proof theory that study the general properties of provable and unprovable statements. In mathematics, a theorem is a statement, often stated in a natural language such as English with mathematical symbols, that is a necessary consequence of explicitly stated or previously agreed assumptions.

In general, the proofs of theorems have two components: a set of premises and a conclusion. The proof of a mathematical theorem is a logical argument demonstrating that the conclusions are a necessary consequence of the premises, in the sense that if the premises are true then the conclusions must also be true, without any further assumptions. The proof of a theorem in a formal sense in logic is a sequence of formulas that are transformed from axioms or formulas generated by some previous transformations.

Although theorems can be written completely in a formal language, for practical reasons, theorems are often expressed in a natural language such as English. The same is true of proofs, which are often expressed as logically organized and clearly worded informal arguments intended to demonstrate that a formal symbolic proof can be constructed. Such arguments are typically easier to check than purely symbolic ones—indeed, many mathematicians would express a preference for a proof that not only demonstrates the validity of a theorem, but also explains in some way why it is obviously true. In some cases, a picture alone may be considered as sufficient to prove a theorem.

Formal and informal notions

A planar map with five colors such that no two regions with the same color meet. It can actually be colored in this way with only four colors. The four color theorem states that such colorings are possible for any planar map, but every known proof involves a computational search that is too long to check by hand.

Logically speaking, most theorems, explicitly or implicitly, are of the form of an indicative conditional: if A, then B. Such a theorem does not state that B is always true, but only that B must be true if A is true. In this case A is called the premises of the theorem and B the conclusion. The theorem "If n is an even natural number then n/2 is a natural number" is a typical example in which the premises is that n is an even natural number and the conclusion is that n/2 is also a natural number.

In order to be proven, a theorem must be expressible as a precise, formal statement. Nevertheless, theorems are usually expressed in a natural language with mathematical symbols, rather than completely in a formal language, with the intention that the reader will be able to produce a formal statement from the informal one. In addition, there are often premises which are understood in context, rather than explicitly stated.

It is common in mathematics to choose a number of premises that are assumed to be true within a given theory, and then declare that the theory consists of all theorems provable using those premises as assumptions. In this case the premises that form the foundational basis are called the axioms (or postulates) of the theory. The field of mathematics known as proof theory studies formal axiom systems and the proofs that can be performed within them.

Some theorems are "trivial," in the sense that they follow from definitions, axioms, and other theorems in obvious ways and do not contain any surprising insights. Some, on the other hand, may be called "deep": their proofs may be long and difficult, involve areas of mathematics superficially distinct from the statement of the theorem itself, or show surprising connections between disparate areas of mathematics. A theorem might be simple to state and yet be deep. An excellent example is Fermat's Last Theorem, and there are many other examples of simple yet deep theorems in number theory and combinatorics, among other areas.

There are other theorems for which a proof is known, but the proof cannot easily be written down. The most prominent examples are the Four color theorem and the Kepler conjecture. Both of these theorems are only known to be true by reducing them to a computational search which is then verified by a computer program. Initially, many mathematicians did not accept this form of proof, but it has become more widely accepted in recent years.

Relation to proof

The notion of a theorem is deeply intertwined with the concept of proof. Indeed, theorems are true precisely in the sense that they possess proofs. Therefore, to establish a mathematical statement as a theorem, the existence of a line of reasoning from axioms in the system (and other, already established theorems) to the given statement must be demonstrated.

Although the proof is necessary to produce a theorem, it is not usually considered part of the theorem. And even though more than one proof may be known for a single theorem, only one proof is required to establish the theorem's validity. The Pythagorean theorem and the law of quadratic reciprocity are contenders for the title of theorem with the greatest number of distinct proofs.

Theorems in logic

Logic, especially in the field of proof theory, considers theorems as statements expressed in some formal language, called formulas or well-formed formulas). A theorem in such a sense is a formula in a deductive system that is generated by transforming axioms by applying rules of inference in the deductive system. Axioms are the formulas to start such transformations and rules of inference determines exactly when a formula can be derived from a set of premises.

Different sets of derivation rules give rise to different interpretations of what it means for an expression to be a theorem. Some derivation rules and formal languages are intended to capture mathematical reasoning; the most common examples use first-order logic. Other deductive systems describe term rewriting, such as the reduction rules for λ calculus.

The definition of theorems as elements of a formal language allows for results in proof theory that study the structure of formal proofs and the structure of provable formulas. The most famous result is Gödel's incompleteness theorem; by representing theorems about basic number theory as expressions in a formal language, and then representing this language within number theory itself, Gödel constructed examples of statements that are neither provable nor disprovable from axiomatizations of number theory.

Relation with scientific theories

Theorems in mathematics and theories in science are fundamentally different in their epistemology. A scientific theory cannot be proven; its key attribute is that it is falsifiable, that is, it makes predictions about the natural world that are testable by experiments. Any disagreement between prediction and experiment demonstrates the incorrectness of the scientific theory, or at least limits its accuracy or domain of validity. Mathematical theorems, on the other hand, are purely abstract formal statements: the proof of a theorem cannot involve experiments or other empirical evidence in the same way such evidence is used to support scientific theories.

The Collatz conjecture: one way to illustrate its complexity is to extend the iteration from the natural numbers to the complex numbers. The result is a fractal, which (in accordance with universality) resembles the Mandelbrot set.

Nonetheless, there is some degree of empiricism and data collection involved in the discovery of mathematical theorems. By establishing a pattern, sometimes with the use of a powerful computer, mathematicians may have an idea of what to prove, and in some cases even a plan for how to set about doing the proof. For example, the Collatz conjecture has been verified for start values up to about 2.88 × 10¹⁸. The Riemann hypothesis has been verified for the first 10 trillion zeroes of the Riemann zeta function. Neither of these statements is considered to be proven.

Such evidence does not constitute proof. For example, the Mertens conjecture is a statement about natural numbers that is now known to be false, but no explicit counterexample (i.e., a natural number n for which the Mertens function M(n) equals or exceeds the square root of n) is known: all numbers less than 10¹⁴ have the Mertens property, and the smallest number which does not have this property is only known to be less than the exponential of 1.59 × 10⁴⁰, which is approximately 10 to the power 4.3 × 10³⁹. Since the number of particles in the universe is generally considered to be less than 10 to the power 100 (a googol), there is no hope to find an explicit counterexample by exhaustive search at present.

Note that the word "theory" also exists in mathematics, to denote a body of mathematical axioms, definitions and theorems, as in, for example, group theory. There are also "theorems" in science, particularly physics, and in engineering, but they often have statements and proofs in which physical assumptions and intuition play an important role; the physical axioms on which such "theorems" are based are themselves falsifiable.

Terminology

Theorems are often indicated by several other terms: the actual label "theorem" is reserved for the most important results, whereas results which are less important, or distinguished in other ways, are named by different terminology.

• A Proposition is a statement not associated with any particular theorem. This term sometimes connotes a statement with a simple proof.
• A Lemma is a "pre-theorem," a statement that forms part of the proof of a larger theorem. The distinction between theorems and lemmas is rather arbitrary, since one mathematician's major result is another's minor claim. Gauss' lemma and Zorn's lemma, for example, are interesting enough per se that some authors present the nominal lemma without going on to use it in the proof of any theorem.
• A Corollary is a proposition that follows with little or no proof from one other theorem or definition. That is, proposition B is a corollary of a proposition A if B can be deduced quickly and easily from A.
• A Claim is a necessary or independently interesting result which may be part of the proof of another statement. Despite the name, claims must be proved.

There are other terms, less commonly used, which are conventionally attached to proven statements, so that certain theorems are referred to by historical or customary names. The following are typical examples.

• Identity, used for theorems which state an equality between two mathematical expressions. Examples include Euler's identity and Vandermonde's identity.
• Rule, used for certain theorems such as Bayes' rule and Cramer's rule that establish useful formulas.
• Law. Examples include the law of large numbers, the law of cosines, and Kolmogorov's zero-one law.
• Principle. Examples include Harnack's principle, the least upper bound principle, and the pigeonhole principle.

A few well-known theorems have even more idiosyncratic names. The name Division algorithm is used for a theorem expressing the outcome of division in the natural numbers and more general rings. The name Banach–Tarski paradox is used for a theorem in measure theory that is paradoxical in the sense that it contradicts common intuitions about volume in three-dimensional space.

A statement which is believed to be true but has not been proven is known as a Conjecture (sometimes a conjecture is also called a hypothesis, but, of course, with a different meaning from the one discussed above). To be considered a conjecture, a statement must usually be proposed publicly, at which point the name of the proponent may be attached to the conjecture, as with Goldbach's conjecture. Other famous conjectures include the Collatz conjecture and the Riemann hypothesis.

Layout

A theorem and its proof are typically laid out as follows:

Theorem (name of person who proved it and year of discovery, proof or publication).

Statement of theorem.

Proof.

Description of proof.

The end of the proof may be signalled by the letters q.e.d. or by one of the tombstone marks "□" or "∎," introduced by Paul Halmos following their usage in magazine articles.

The exact style will depend on the author or publication. Many publications provide instructions or macros for typesetting in the house style.

It is common for a theorem to be preceded by definitions describing the exact meaning of the terms used in the theorem. It is also common for a theorem to be preceded by a number of propositions or lemmas which are then used in the proof. However, lemmas are sometimes embedded in the proof of a theorem, either with nested proofs, or with their proofs presented after the proof of the theorem.

Corollaries to a theorem are either presented between the theorem and the proof, or directly after the proof. Sometimes corollaries have proofs of their own which explain why they follow from the theorem.

Trivia

It has been estimated that over a quarter of a million theorems are proved every year.

The well-known aphorism that "A mathematician is a device for turning coffee into theorems" is probably due to Alfréd Rényi, although it is often attributed to Rényi's colleague Paul Erdős (and Rényi may have been thinking of Erdős), who was famous for the many theorems he produced, the Erdos number|number of his collaborations, and his coffee drinking.

The classification of finite simple groups is regarded by some to be the longest proof of a theorem; it comprises tens of thousands of pages in 500 journal articles by some 100 authors. These papers are together believed to give a complete proof, and there are several ongoing projects to shorten and simplify this proof.

References

ISBN links support NWE through referral fees

• Enderton, H. B. 2000. A Mathematical Introduction to Logic, 2nd Edition. Academic Press.
• Hoffman, P. 1998. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. Hyperion, New York.
• Petkovsek, Marko, Herbert Wilf, and Doron Zeilberger. 1996. "A = B" A.K. Peters, Wellesley, Massachusetts.

External links

All links retrieved April 30, 2023.

• Stanford Encyclopedia entries on logic

General Philosophy Sources

• Stanford Encyclopedia of Philosophy
• The Internet Encyclopedia of Philosophy
• Paideia Project Online
• Project Gutenberg

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Theorem  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Theorem"

Note: Some restrictions may apply to use of individual images which are separately licensed.