Definition

A definition is a statement of the meaning of a term, word or phrase. The term to be defined is known as the definiendum (Latin: that which is to be defined). The words which define it are known as the definiens (Latin: that which is doing the defining). Definitions have various kinds of features and can be distinguished as such. The list of important kinds of definitions is as follows:

• Descriptive and Stipulative Definitions: A descriptive definition gives the meaning of a given term in general use and a stipulative definition gives a new meaning to a term already in use or a new term.
• Intensional and Extensional Definitions: A intensional definition specifies the necessary and sufficient conditions for a thing to be a member of a specific set. A extensional definition of a term specifies the extension of the term.
• Defnition by genus and differentia: A definition by genus and differentia specifies the genus and differentia of the definiens.
• Genetic Definition: A genetic definition describes the process or method by which the definiens is formed.
• Recursive Definitions: A recursive definition is one that defines a word in terms of itself, so to speak, in some non-circular way.

Given that a natural language such as English contains, at any given time, a finite number of words, any comprehensive list of definitions must either be circular or leave some terms undefined.

Descriptive and Stipulative definitions

A definition may either give the meaning that a term bears in general use (a descriptive definition), or that which the speaker intends to impose upon it for the purpose of his or her discourse (a stipulative definition). Stipulative definitions differ from descriptive definitions in that they prescribe a new meaning either to a term already in use or to a new term. A descriptive definition can be shown to be right or wrong by comparison to usage, while a stipulative definition cannot. A stipulative definition, however, may be more or less useful. A persuasive definition, named by C.L. Stevenson, is a form of stipulative definition which purports to describe the 'true' or 'commonly accepted' meaning of a term, while in reality stipulating an altered use, perhaps as an argument for some view, for example that some system of government is democratic. Stevenson also notes that some definitions are 'legal' or 'coercive', whose object is to create or alter rights, duties or crimes.

Intensional and Extension Definitions

An intensional definition, also called a connotative definition, specifies the necessary and sufficient conditions for a thing being a member of a specific set. Any definition that attempts to set out the essence of something, such as that by genus and differentia, is an intensional definition.

An extensional definition, also called a denotative definition, of a concept or term specifies its extension. It is, a list naming every object that is a member of a specific set.

So, for example, an intensional definition of 'Prime Minister' might be the most senior minister of a cabinet in the executive branch of government in a parliamentary system; whereas an extensional definition would be simply a list of all past and present Prime Ministers.

One form of extensional definition is ostensive definition. This gives the meaning of a term by pointing, in the case of an individual, to the thing itself, or in the case of a class, to examples of the right kind. So you can explain who Alice (an individual) is by pointing her out to me; or what a rabbit (a class) is by pointing at several and expecting me to 'catch on'. The process of ostensive definition itself was critically appraised by Ludwig Wittgenstein.

An enumerative definition of a concept or term is an extensional definition that gives an explicit and exhaustive listing of all the objects that fall under the concept or term in question. Enumerative definitions are only possible for finite sets and only practical for relatively small sets.

Definition by genus and differentia

Scientific classification of living things uses definition by genus and differentia.

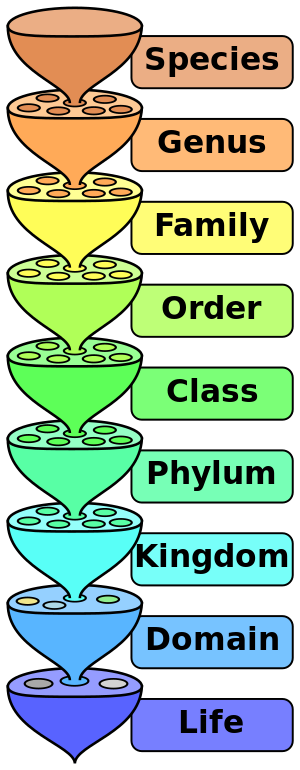
Traditionally, a definition consists of the genus (the family) of thing to which the defined thing belongs, and the differentia (the distinguishing feature which marks it off from other members of the same family). Thus 'triangle' is defined as 'a plane figure (genus) bounded by three straight sides (differentia).

Rules for definition by genus and differentia

Certain rules have traditionally been given for this particular type of definition.

1. A definition must set out the essential attributes of the thing defined.
2. Definitions should avoid circularity. To define a horse as 'a member of the species equus' would convey no information whatsoever. For this reason, Locke adds that a definition of a term must not consist of terms which are synonymous with it. This error is known as circulus in definiendo. Note, however, that it is acceptable to define two relative terms in respect of each other. Clearly, we cannot define 'antecedent' without using the term 'consequent', nor conversely.
3. The definition must not be too wide or too narrow. It must be applicable to everything to which the defined term applies (i.e. not miss anything out), and to no other objects (i.e. not include any things to which the defined term would not truly apply).
4. The definition must not be obscure. The purpose of a definition is to explain the meaning of a term which may be obscure or difficult, by the use of terms that are commonly understood and whose meaning is clear. The violation of this rule is known by the Latin term obscurum per obscurius. However, sometimes scientific and philosophical terms are difficult to define without obscurity.
5. A definition should not be negative where it can be positive. We should not define 'wisdom' as the absence of folly, or a healthy thing as whatever is not sick. Sometimes this is unavoidable, however. We cannot define a point except as 'something with no parts', nor blindness except as 'the absence of sight in a creature that is normally sighted'.

Essence

In classical thought, a definition was taken to be a statement of the essence of a thing. Aristotle had it that an object's essential attributes form its "essential nature," and that a definition of the object must include these essential attributes.

The idea that a definition should state the essence of a thing led to the distinction between nominal and real essence, originating with Aristotle. In a passage from the Posterior Analytics, he says that we can know the meaning of a made-up name (he gives the example 'goat stag'), without knowing what he calls the 'essential nature' of the thing that the name would denote, if there were such a thing. This led medieval logicians to distinguish between the so-called quid nominis or 'whatness of the name', and the underlying nature common to all the things it names, which they called the quid rei or 'whatness of the thing'. (Early modern philosophers like Locke used the corresponding English terms 'nominal essence' and 'real essence'). The name 'hobbit', for example, is perfectly meaningful. It has a quid nominis. But we could not know the real nature of hobbits, even if there were such things, and so we cannot know the real nature or quid rei of hobbits. By contrast, the name 'man' denotes real things (men) that have a certain quid rei. The meaning of a name is distinct from the nature that thing must have in order that the name apply to it.

This leads to a corresponding distinction between nominal and real definition. A nominal definition is the definition explaining what a word means, i.e. which says what the 'nominal essence' is, and is definition in the classical sense as given above. A real definition, by contrast, is one expressing the real nature or quid rei of the thing.

Genetic definition

A genetic definition describes the process or method by which a thing is formed.

But if you define the circle as a pattern resulting from having a segment of a line revolve around one of its ends, this is a genetic definition because it tells you how to make a circle.

Recursive definitions

A recursive definition, sometimes also called an inductive definition, is one that defines a word in terms of itself, so to speak, albeit in a useful way. Normally this consists of three steps:

1. At least one thing is stated to be a member of the set being defined; this is sometimes called a "base set."
2. All things bearing a certain relation to other members of the set are also to count as members of the set. It is this step that makes the definition recursive.
3. All other things are excluded from the set

For instance, we could define natural number as follows (after Peano):

1. "0" is a natural number.
2. Each natural number has a distinct successor, such that:
   • the successor of a natural number is also a natural number, and
   • no natural number is succeeded by "0."
3. Nothing else is a natural number.

So "0" will have exactly one successor, which for convenience we can call "1." In turn, "1" will have exactly one successor, which we would call "2," and so on. Notice that the second condition in the definition itself refers to natural numbers, and hence involves self-reference. Although this sort of definition may seem to involve a form of circularity, it is not vicious, and the definition is quite successful.

Limitations of definition

Given that a natural language such as English contains, at any given time, a finite number of words, any comprehensive list of definitions must either be circular or leave some terms undefined. If every term of every definiens must itself be defined, where should we stop? A dictionary, for instance, insofar as it is a comprehensive list of lexical definitions, must resort to circularity.

Many philosophers have chosen instead to leave some terms undefined. The scholastic philosophers claimed that the highest genera (the so-called ten generalissima) cannot be defined, since we cannot assign any higher genus under which they may fall. Thus we cannot define being, unity and similar concepts. Locke supposes in An Essay Concerning Human Understanding that the names of simple concepts do not admit of any definition. More recently Bertrand Russell sought to develop a formal language based on logical atoms. Other philosophers, notably Wittgenstein, rejected the need for any undefined simples. Wittgenstein pointed out in his Philosophical Investigations that what counts as a "simple" in one circumstance might not do so in another. He rejected the very idea that every explanation of the meaning of a term needed itself to be explained: "As though an explanation hung in the air unless supported by another one", claiming instead that explanation of a term is only needed when we need to avoid misunderstanding.

Locke and Mill also argued that we cannot define individuals. We learn names by connecting an idea with a sound, so that speaker and hearer have the same idea when the same word is used. This is not possible when no one else is acquainted with the particular thing that has "fallen under our notice". Russell offered his theory of descriptions in part as a way of defining a proper name, the definition being given by a definite description that "picks out" exactly one individual. Saul Kripke pointed to difficulties with this approach, especially in relation to modality, in his book Naming and Necessity.

There is a presumption in the classic example of a definition that the definiens can be stated. Wittgenstein argued that for some terms this is not the case. The examples he used include game, number and family. In such cases, he argued, there is no fixed boundary that can be used to provide a definition. Rather, the items are grouped together because of a family resemblance. For terms such as these it is not possible to state a definition; rather, one simply comes to understand the use of the term.

See also

• Analytic proposition

References

ISBN links support NWE through referral fees

• Copi, Irving. Introduction to Logic. New York: Macmillan, 1982. ISBN 0029775205
• Joseph, Horace William Brindley. An Introduction to Logic, 2nd ed. Clarendon Press repr. Paper Tiger, 2000 (original 1916). ISBN 1889439177 full text of 1st ed. Retrieved June 8, 2020.
• Joyce, George Hayward. Principles of logic, 3rd ed., new impression. London, New York: Longmans, Green and co., 1926.
• McKean, Erin. Verbatim: From the bawdy to the sublime, the best writing on language for word lovers, grammar mavens, and armchair linguists. Harvest Books, 2001. ISBN 015601209X
• Simpson, John and Edmund Weiner. Oxford English Dictionary, 2nd ed. (20 volumes). Oxford University Press, 1989. ISBN 0198611862
• Wittgenstein, Ludwig. Philosophical Investigations. Blackwell Publishing, 2001 (original 1953). ISBN 0631231277

External links

All links retrieved January 28, 2024.

• The Definition of Definitions By Dr. Sam Vaknin

General Philosophy Sources

• Stanford Encyclopedia of Philosophy
• The Internet Encyclopedia of Philosophy
• Paideia Project Online
• Project Gutenberg

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• definition  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Definition"

Note: Some restrictions may apply to use of individual images which are separately licensed.