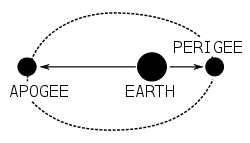
Apsis
- "Apogee," "Perigee," "Aphelion," "Perihelion" redirect here.
When a celestial object is in an elliptical orbit around another body, an apsis (plural apsides) is a point on the orbit at greatest or least distance from the center of attraction, which is generally the center of mass of the system. The point of closest approach is called the periapsis or pericenter, and the point of farthest excursion is called the apoapsis, apapsis, or apocenter. (In technical usage, the words periapsis and apoapsis are preferred over pericenter and apocenter.) A straight line drawn through the periapsis and apoapsis is called the line of apsides, corresponding to the major axis of the ellipse, that is, the line through the longest part of the ellipse.
Derivative terms are used to identify the body being orbited. The most common are perigee and apogee, which refer to points on orbits around the Earth, and perihelion and aphelion, which refer to points on orbits around the Sun. The terms perihelion and aphelion are commonly used for orbits of planets in the Solar System, but the same terms are occasionally employed when referring to the nearest and farthest distances of a comet from the Sun. During the Apollo program, the terms pericynthion and apocynthion were used when referring to the spacecraft's orbit around the Moon.
Etymology
The term apsis is derived from the Latin word apsis, meaning "arch" or "vault," which can be traced back to the Greek word hapsis, meaning "loop" or "arch," from Greek haptein, meaning "fasten together." The prefixes peri and apo can be traced back to Greek terms that mean "near" and "away from," respectively.[1]
In the case of perigee and apogee, the root gee comes from the Greek gê, meaning "Earth." For perihelion and aphelion, the root helion is derived from the Greek helios, meaning "Sun."
Additional terminology
As noted above, "-gee" and "-helion" are used for orbits of objects around the Earth and the Sun, respectively. Various additional terms have been coined for orbits around other celestial objects. For example, "-astron" and "-galacticon" are used when the body being orbited is a star or a galaxy, respectively. For orbits around a black hole, physicist Geoffrey A. Landis introduced the terms perimelasma and apomelasma (from the Greek root) in 1998; but later (in 2002), the terms perinigricon and aponigricon (from the Latin) appeared in the scientific literature.
Various terms are listed in the table below. Although some of them are used occasionally, the term -saturnium has rarely been used in the last 50 years. Also, the -gee form is commonly (albeit incorrectly) used as a generic term for "closest or farthest point from a planet," instead of specifically applying to orbits around the Earth.
| Body | Closest approach | Farthest approach |
|---|---|---|
| Galaxy | Perigalacticon | Apogalacticon |
| Star | Periastron | Apastron |
| Black hole | Perimelasma/Peribothra/Perinigricon | Apomelasma/Apobothra/Aponigricon |
| Sun | Perihelion | Aphelion[2] |
| Mercury | Perihermion | Apohermion |
| Venus | Pericytherion/Pericytherean/Perikrition | Apocytherion/Apocytherean/Apokrition |
| Earth | Perigee | Apogee |
| Moon | Periselene/Pericynthion/Perilune | Aposelene/Apocynthion/Apolune |
| Mars | Periareion | Apoareion |
| Jupiter | Perizene/Perijove | Apozene/Apojove |
| Saturn | Perikrone/Perisaturnium | Apokrone/Aposaturnium |
| Uranus | Periuranion | Apouranion |
| Neptune | Periposeidion | Apoposeidion |
| Pluto | Perihadion | Apohadion |
Given that "peri" and "apo" are derived from Greek, it is considered by some purists[3] more correct to use the Greek form for the body, giving forms such as "-zene" for Jupiter and "-krone" for Saturn. The daunting prospect of having to maintain a different word for every orbitable body in the solar system (and beyond) is the main reason why the generic '-apsis' has become the almost universal norm.
- In the case of the Moon, in practice all three forms are used, albeit very infrequently. The "-cynthion" form is, according to some, reserved for artificial bodies, whereas others reserve "-lune" for an object launched from the Moon and "-cynthion" for an object launched from elsewhere. The "-cynthion" form was the version used in the Apollo Project, following a NASA decision in 1964.
- For Venus, the form "-cytherion" is derived from the commonly used adjective "cytherean;" the alternate form "-krition" (from Kritias, an older name for Aphrodite) has also been suggested.
- For Jupiter, the "-jove" form is occasionally used by astronomers whereas the "-zene" form is never used, like the other pure Greek forms ("-areion" (Mars), "-hermion" (Mercury), "-krone" (Saturn), "-uranion" (Uranus), "-poseidion" (Neptune) and "-hadion" (Pluto)).
Earth's perihelion and aphelion
The Earth is closest to the Sun in early January and farthest in early July. The relation between perihelion, aphelion and the Earth's seasons changes over a 21,000 year cycle. This anomalistic precession contributes to periodic climate change (related to what are known as Milankovitch cycles).
The day and hour of these events for recent and upcoming years are noted in the table below.[4]
| Year | Perihelion | Aphelion |
|---|---|---|
| 2007 | January 3 20Z | July 7 00Z |
| 2008 | January 3 00Z | July 4 08Z |
| 2009 | January 4 15Z | July 4 02Z |
| 2010 | January 3 00Z | July 6 11Z |
| 2011 | January 3 19Z | July 4 15Z |
| 2012 | January 5 00Z | July 5 03Z |
| 2013 | January 2 05Z | July 5 15Z |
| 2014 | January 4 12Z | July 4 00Z |
| 2015 | January 4 07Z | July 6 19Z |
| 2016 | January 2 23Z | July 4 16Z |
Mathematical formulae
The following mathematical formulae characterize the periapsis and apoapsis of an orbit:
- Periapsis: maximum speed at minimum (periapsis) distance
- Apoapsis: minimum speed at maximum (apoapsis) distance
while, in accordance with Kepler's laws of planetary motion (conservation of angular momentum) and the conservation of energy, these quantities are constant for a given orbit:
- Specific relative angular momentum
- Specific orbital energy
where:
- is the semi-major axis
- is the standard gravitational parameter
- is the eccentricity, defined as
Note that for conversion from heights above the surface to distances between an orbit and its primary, the radius of the central body has to be added, and conversely.
The arithmetic mean of the two limiting distances is the length of the semi-major axis . The geometric mean of the two distances is the length of the semi-minor axis .
The geometric mean of the two limiting speeds is , the speed corresponding to a kinetic energy which, at any position of the orbit, added to the existing kinetic energy, would allow the orbiting body to escape (the square root of the product of the two speeds is the local escape velocity).
See also
Notes
- ‚ÜĎ Online Etymology Dictionary, Homepage. Retrieved November 14, 2008.
- ‚ÜĎ Properly pronounced "affelion" because the (neo) Greek is őĪŌÜőģőĽőĻőŅőĹ, although the hypercorrection "ap-helion" is commonly heard.
- ‚ÜĎ National Solar Observatgory, Apsis, Glossary of Terms. Retrieved November 14, 2008.
- ‚ÜĎ U.S. Naval Observatory, Earth's Seasons: Equinoxes, Solstices, Perihelion, and Aphelion, 2000-2020, Astronomical Applications Department. Retrieved November 14, 2008.
ReferencesISBN links support NWE through referral fees
- Bate, Roger R., Donald D. Mueller, and Jerry E. White. 1971. Fundamentals of Astrodynamics. New York: Dover Publications. ISBN 0486600610.
- Montenbruck, Oliver, and Gill Eberhard. 2000. Satellite Orbits: Models, Methods, and Applications. Berlin: Springer. ISBN 978-3540672807.
- Open University. 1990. Planetary Orbits. Mathematical Models and Methods, Unit 30. Milton Keynes, UK: Open University. ISBN 0749220368.
- Rees, Martin J. (ed.). 2008. Universe. New York, NY: DK. ISBN 978-0756636708.
- Seeds, Michael A. 2008. The Solar System, 6th ed. Belmont, CA: Thomson Brooks/Cole. ISBN 978-0495387879.
- Vallado, David Anthony, and Wayne D. McClain. 2001. Fundamentals of Astrodynamics and Applications. Space Technology Library, 12. Dordrecht, The Netherlands: Kluwer Academic Publishers. ISBN 1881883124.
External links
All links retrieved August 11, 2023.
- Full Moon at Apogee and Perigee. Lunar Image Gallery. (Photographic Size Comparison.)
- Sun at Aphelion and Perihelion. Solar Image Gallery. (Photographic Size Comparison.)
| ||||||||||||||||||||||||||||||||||||||||||||||
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.