Uncertainty

Certainty series
Nihilism Agnosticism Uncertainty Justification Probability Estimation Belief Certainty Determinism

Uncertainty is a term used in subtly different ways in a number of fields, including philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science. It applies to predictions of future events, physical measurements already made, or to the unknown.

The philosophical problematics of uncertainty are often tied to a number of conditions: Fallibility of human beings; the limit of knowability of or accessibility to the past and future; contingency and spontaneity of human decisions and actions that affect social pheneomena. Uncertainty, thus, has both ontological and epistemological elements that appear in various ways in social, historical, cultural phenomena and our understanding of these and other types of phenomena (including natural phenomena). The question of uncertainty can also be discussed in reference to belief and faith.

Concepts

Philosophy and religion

Philosophy tries to establish certain valid principles with certainty. Be it agnosticism or skepticism, it tries to establish "unknowability" or uncertainty of knowledge or a limit of cognitive capabilities of human being as the valid principle. If, on the contrary, skepticism is skeptical about its position, it is self-defeating and it cannot establish its position. Thus, a quest for certain knowledge or valid knowledge exists at the root of philosophical inquiries. Conversely, philosophical inquiries begin with the fundamental insight or conviction that human being is fallible and knowledge always have some element of uncertainty. Philosophers, thus, inquired into a way to get to the valid philosophical claims.

In religious philosophy, uncertainty of knowledge is rooted in the insight that human being is fallible. Religious philosophers present faith, belief, and revelation as a way to overcome the limitation of fallibility and reach valid knowledge.

Philosophers also tried to find some methods, such as phenomenology,linguistic analysis, or certain areas such as language by which we can gain certain knowledge. Philosophical methodologies and epistemological perspectives have been presented as ways to gain knowledge.

In some views, the question of uncertainty also arises from the temporal limits of existence. Both events in the past and those in the future are not accessible to us; the past is always reconstructed by some hermeneutic schema. The reconstructed past is always selective, partial, and interpretive, hence it essentially retains some degree of uncertainty. The future is also uncertain for human action and natural phenomena is contingent and spontaneous.

As understood by Heidegger, human beings exist with the realistic possibility of death; uncertainty and anxiety are thus essential to human existence.

Social and natural sciences

In his seminal work, Risk, Uncertainty, and Profit University of Chicago economist Frank Knight (1921) established the important distinction between risk and uncertainty:

Uncertainty must be taken in a sense radically distinct from the familiar notion of risk, from which it has never been properly separated…. The essential fact is that "risk" means in some cases a quantity susceptible of measurement, while at other times it is something distinctly not of this character; and there are far-reaching and crucial differences in the bearings of the phenomena depending on which of the two is really present and operating…. It will appear that a measurable uncertainty, or "risk" proper, as we shall use the term, is so far different from an unmeasurable one that it is not in effect an uncertainty at all.

Although the terms are used in various ways among the general public, many specialists in decision theory, statistics and other quantitative fields have defined uncertainty and risk more specifically. Doug Hubbard defines uncertainty and risk as:

1. Uncertainty: The lack of certainty, A state of having limited knowledge where it is impossible to exactly describe existing state or future outcome, more than one possible outcome.
2. Measurement of Uncertainty: A set of possible states or outcomes where probabilities are assigned to each possible state or outcome—this also includes the application of a probability density function to continuous variables
3. Risk: A state of uncertainty where some possible outcomes have an undesired effect or significant loss.
4. Measurement of Risk: A set of measured uncertainties where some possible outcomes are losses, and the magnitudes of those losses—this also includes loss functions over continuous variables.

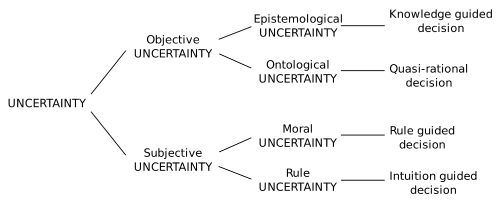
There are other different taxonomy of uncertainties and decisions that include a more broad sense of uncertainty and how it should be approached. The following diagram illustrates one possible classification and approach (other classifications and approaches are possible):

Example: an uncertainty Taxonomy

For example, if it is not known whether it will rain tomorrow, then you are in a state of uncertainty. If you apply probabilities to the possible outcomes using weather forecasts or even just a calibrated probability assessment, you will have quantified the uncertainty. Suppose you quantify your uncertainty as a 90 percent chance of sunshine. If you are planning a major, costly, outdoor event for tomorrow then you have risk since there is a 10 percent chance of rain and rain would be undesirable. Furthermore, if this is a business event and you would lose $100,000 if it rains, then you have quantified the risk (a 10 percent chance of losing $100,000). These situation can be made even more realistic by quantifying light rain vs. heavy rain, the cost of delays vs. outright cancellation, and so on.

Some may represent the risk in this example as the "expected opportunity loss" (EOL) or the chance of the loss multiplied by the amount of the loss (10% x $100,000 = $10,000). That is useful if the organizer of the event is "risk neutral" which most people are not. Most would be willing to pay a premium to avoid the loss. An insurance company, for example, would compute an EOL as a minimum for any insurance coverage, then add on to that other operating costs and profit. Since many people are willing to buy insurance for many reasons, then clearly the EOL alone is not the perceived value of avoiding the risk.

Quantitative uses of the terms uncertainty and risk are fairly consistent from fields such as probability theory, actuarial science, and information theory. Some also create new terms without substantially changing the definitions of uncertainty or risk. For example, surprisal is a variation on uncertainty sometimes used in information theory. But outside of the more mathematical uses of the term, usage may vary widely. In cognitive psychology, uncertainty can be real, or just a matter of perception, such as expectations, threats, and so on.

Vagueness or ambiguity are sometimes described as "second order uncertainty," where there is uncertainty even about the definitions of uncertain states or outcomes. The difference here is that this uncertainty is about the human definitions and concepts not an objective fact of nature. It has been argued that ambiguity, however, is always avoidable while uncertainty (of the "first order" kind) is not necessarily avoidable.

Uncertainty may be purely a consequence of a lack of knowledge of obtainable facts. That is, you may be uncertain about whether a new rocket design will work, but this uncertainty can be removed with further analysis and experimentation. At the subatomic level, however, uncertainty may be a fundamental and unavoidable property of the universe. In quantum mechanics, the Heisenberg Uncertainty Principle puts limits on how much an observer can ever know about the position and velocity of a particle. This may not just be ignorance of potentially obtainable facts but that there is no fact to be found. There is some controversy in physics as to whether such uncertainty is an irreducible property of nature or if there are "hidden variables" that would describe the state of a particle even more exactly than Heisenberg's uncertainty principle allows.

Measurements

In metrology, physics, and engineering, the uncertainty or margin of error of a measurement is stated by giving a range of values which are likely to enclose the true value. This may be denoted by error bars on a graph, or by the following notations:

• Measured value ± uncertainty
• Measured value (uncertainty)

The latter "concise notation" is used for example by IUPAC in stating the atomic mass of elements. There, the uncertainty applies only to the least significant figure of x. For instance, 1.00794(7) stands for 1.00794 ± 0.00007.

Often, the uncertainty of a measurement is found by repeating the measurement enough times to get a good estimate of the standard deviation of the values. Then, any single value has an uncertainty equal to the standard deviation. However, if the values are averaged, then the mean measurement value has a much smaller uncertainty, equal to the standard error of the mean, which is the standard deviation divided by the square root of the number of measurements.

When the uncertainty represents the standard error of the measurement, then about 68.2 percent of the time, the true value of the measured quantity falls within the stated uncertainty range. For example, it is likely that for 31.8 percent of the atomic mass values given on the list of elements by atomic mass, the true value lies outside of the stated range. If the width of the interval is doubled, then probably only 4.6 percent of the true values lie outside the doubled interval, and if the width is tripled, probably only 0.3 percent lie outside. These values follow from the properties of the normal distribution, and they apply only if the measurement process produces normally distributed errors. In that case, the quoted standard errors are easily converted to 68.3 percent ("one sigma"), 95.4 percent ("two sigma"), or 99.7 percent ("three sigma") confidence intervals.

In this context, uncertainty depends on both the accuracy and precision of the measurement instrument. The least the accuracy and precision of an instrument are, the larger the measurement uncertainty is. Notice that precision is often determined as the standard deviation of the repeated measures of a given value, namely using the same method described above to assess measurement uncertainty. However, this method is correct only when the instrument is accurate. When it is inaccurate, the uncertainty is larger than the standard deviation of the repeated measures, and it appears evident that the uncertainty does not depend only on instrumental precision.

Applications

• In metrology, measurement uncertainty is a central concept quantifying the dispersion one may reasonably attribute to a measurement result. Such an uncertainty can also be referred to as a measurement error. In daily life, measurement uncertainty is often implicit ("He is 6 feet tall" give or take a few inches), while for any serious use an explicit statement of the measurement uncertainty is necessary. The expected measurement uncertainty of many measuring instruments (scales, oscilloscopes, force gages, rulers, thermometers, etc) is often stated in the manufacturers specification.

The most commonly used procedure for calculating measurement uncertainty is described in the Guide to the Expression of Uncertainty in Measurement (often referred to as "the GUM") published by ISO. A derived work is for example the National Institute for Standards and Technology (NIST) publication NIST Technical Note 1297 "Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results" and the Eurachem/Citac publication "Uncertatinty in measurements" (available at the Eurachem homepage). The uncertainty of the result of a measurement generally consists of several components. The components are regarded as random variables, and may be grouped into two categories according to the method used to estimate their numerical values:

• Type A, those which are evaluated by statistical methods,
• Type B, those which are evaluated by other means, for example, by assigning a probability distribution.

By propagating the variances of the components through a function relating the components to the measurement result, the combined measurement uncertainty is given as the square root of the resulting variance. The simplest form is the standard deviation of a repeated observation.

• In weather forecasting it is now commonplace to include data on the degree of uncertainty in a weather forecast.
• In physics in certain situations, uncertainty has been elevated into a principle, the uncertainty principle.
• In scientific modelling, in which the prediction of future events should be understood to have a range of expected values.
• Uncertainty is used in engineering notation when talking about significant figures. Or the possible error involved in measuring things such as distance.
• Uncertainty is designed into games, most notably in gambling, where chance is central to play.
• Uncertainty is often an important factor in economics. According to economist Frank Knight, it is different from risk, where there is a specific probability assigned to each outcome (as when flipping a fair coin). Uncertainty involves a situation that has unknown probabilities, while the estimated probabilities of possible outcomes need not add to unity.
• Investing in financial markets such as the stock market.
• In risk assessment and risk management.
• Uncertainty has been a common theme in art, both as a thematic device (see, for example, the indecision of Hamlet), and as a quandary for the artist (such as Martin Creed's difficulty with deciding what artworks to make).

See also

• Certainty
• Fuzzy logic
• Game theory
• Information
• Information theory
• Statistics
• Statistical mechanics
• Uncertainty principle

References

ISBN links support NWE through referral fees

• Flyvbjerg, B. "From Nobel Prize to Project Management: Getting Risks Right." Project Management Journal 37 (3): 5-15. Retrieved January 6, 2016.
• Galbraith, John Kenneth. The Age of Uncertainty. Boston: Houghton Mifflin, 1977. ISBN 9780395249000.
• Gigerenzer, Gerd. Calculated Risks: How to Know When Numbers Deceive You. New York: Simon & Schuster, 2002. ISBN 9780743205566.
• Halpern, Joseph Y. Reasoning About Uncertainty. Cambridge, MA: MIT Press, 2003. ISBN 9780262083201.
• Hubbard, Douglas W. How to Measure Anything: Finding the Value of "Intangibles" in Business. Hoboken, NJ: John Wiley & Sons, 2007. ISBN 9780470110126.
• Kalman, Maira. The Principles of Uncertainty. New York: Penguin Press, 2007.
• Knight, Frank H. Risk, Uncertainty and Profit. New York: Augustus M. Kelley, 1964. ISBN 9781594201349.
• Lindley, D. V. Understanding Uncertainty. Hoboken, N.J.: Wiley, 2006. ISBN 9780470043837.
• Tannert, Christof, Horst-Dietrich Elvers, and Burkhard Jandrig.2007. "The ethics of uncertainty. In the light of possible dangers, research becomes a moral duty." EMBO Reports 8 (10): 892-896.

External links

All links retrieved May 2, 2023.

• Proposal for a New Error Calculus
• Bibliography of Papers Regarding Measurement Uncertainty
• Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results
• Strategic Engineering: Designing Systems and Products under Uncertainty (MIT Research Group)
• Uri Weiss, The Regressive Effect of Legal Uncertainty, 2005.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Uncertainty  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Uncertainty"

Note: Some restrictions may apply to use of individual images which are separately licensed.