Abacus
An abacus (plurals abacuses or abaci), also called a counting frame, is a calculating tool for performing arithmetical processes, often constructed as a wooden frame with beads sliding on wires. The user, called an abacist, slides counters by hand on rods or in grooves. It was in use centuries before the adoption of the written Hindu-Arabic numeral system and is still widely used by merchants and clerks in China, Japan, Africa and elsewhere.
The abacus is a simple, inexpensive, yet powerful tool for calculation. Although electronic calculators are replacing it for practical reasons, the use of the abacus continues to be taught in technologically advanced countries such as Japan. Just as with popular board games such as chess, shogi, and go, local, regional, and national competitions in abacus use are held for students.
Origins
The first abacus was most likely based on a flat stone covered with sand or dust. Words and letters were drawn in the sand; eventually numbers were added and pebbles used to aid calculations. The Babylonians used this dust abacus as early as 2400 B.C.E.[1] The origin of the counter abacus with strings is obscure, but India, Mesopotamia or Egypt are seen as probable points of origin.[2] China played an essential part in the development and evolution of the abacus.
From this, a variety of abaci were developed; the most popular were based on the bi-quinary system, using a combination of two bases (base-2 and base-5) to represent decimal numbers. But the earliest abaci used first in Mesopotamia and later by scribes in Egypt and Greece used sexagesimal numbers represented with factors of 5, 2, 3, and 2 for each digit.
The use of the word abacus dates from before 1387, when a Middle English work borrowed the word from Latin to describe a sandboard abacus. The Latin word came from abakos, the Greek genitive form of abax ("calculating-table"). Because abax also had the sense of "table sprinkled with sand or dust, used for drawing geometric figures," some linguists speculate that the Greek word may be derived from a Semitic root, ābāq (pronounced "a-vak"), the Hebrew word for "dust." Though details of the transmission are obscure, it may also be derived from the Phoenician word abak, meaning "sand." The preferred plural of abacus is a subject of disagreement, but both abacuses[3] and abaci[4] are in use.
Babylonian abacus
Babylonians may have used the abacus for addition and subtraction. However, this primitive device proved difficult to use for more complex calculations.[5] Some scholars point to a character from the Babylonian cuniform which may have been derived from a representation of the abacus.[6]
Egyptian abacus
The use of the abacus in ancient Egypt is mentioned by the Greek historian Herodotus, who writes that the manner of its usage by the Egyptians was opposite in direction when compared with the Greek method. Archaeologists have found ancient disks of various sizes that are thought to have been used as counters. However, wall depictions of this instruments have not been discovered, casting some doubt over the extent of use of this instrument.[2]
Greek abacus
A tablet found on the Greek island Salamis in 1846 dates back to 300 B.C.E., making it the oldest counting board discovered so far. It is a slab of white marble 149 cm long, 75 cm wide, and 4.5 cm thick, on which are 5 groups of markings. In the center of the tablet is a set of 5 parallel lines equally divided by a vertical line, capped with a semi-circle at the intersection of the bottom-most horizontal line and the single vertical line. Below these lines is a wide space with a horizontal crack dividing it. Below this crack is another group of eleven parallel lines, again divided into two sections by a line perpendicular to them, but with the semi-circle at the top of the intersection; the third, sixth and ninth of these lines are marked with a cross where they intersect with the vertical line.
Roman abacus
The normal method of calculation in ancient Rome, as in Greece, was by moving counters on a smooth table. Originally pebbles, calculi, were used. Later, and in medieval Europe, jetons were manufactured. Marked lines indicated units, fives, tens etc. as in the Roman numeral system. This system of 'counter casting' continued into the late Roman empire and in medieval Europe, and persisted in limited use into the nineteenth century.[7]
In addition to the more common method using loose counters, several specimens have been found of a Roman abacus, shown here in reconstruction. It has eight long grooves containing up to five beads in each and eight shorter grooves having either one or no beads in each.
The groove marked I indicates units, X tens, and so on up to millions. The beads in the shorter grooves denote fives—five units, five tens, etc., essentially in a bi-quinary coded decimal system, obviously related to the Roman numerals. The short grooves on the right may have been used for marking Roman ounces.
Indian abacus
First century sources, such as the Abhidharmakosa describe the knowledge and use of abacus in India.[8] Around the fifth century, Indian clerks were already finding new ways of recording the contents of the Abacus.[9] Hindu texts used the term shunya (means Zero) to indicate the empty column on the abacus.[10]
Chinese abacus
The earliest mention of a suanpan is found in a first century book of the Eastern Han Dynasty, namely Supplementary Notes on the Art of Figures written by Xu Yue.[11] However, the exact design of this suanpan is not known.
Usually, a suanpan is about 20 cm tall and it comes in various widths depending on the operator. It usually has more than seven rods. There are two beads on each rod in the upper deck and five beads each in the bottom for both decimal and hexadecimal computation. The beads are usually rounded and made of a hardwood. The beads are counted by moving them up or down towards the beam. The suanpan can be reset to the starting position instantly by a quick jerk along the horizontal axis to spin all the beads away from the horizontal beam at the center.
Suanpans can be used for functions other than counting. Unlike the simple counting board used in elementary schools, very efficient suanpan techniques have been developed to do multiplication, division, addition, subtraction, square root and cube root operations at high speed.
In the famous long scroll Riverside Scenes at Qingming Festival painted by Zhang Zeduan (1085-1145) during the Song Dynasty (960-1297), a suanpan is clearly seen lying beside an account book and doctor's prescriptions on the counter of an apothecary's (Feibao).
The similarity of the Roman abacus to the Chinese one suggests that one could have inspired the other, as there is some evidence of a trade relationship between the Roman Empire and China. However, no direct connection can be demonstrated, and the similarity of the abaci may be coincidental, both ultimately arising from counting with five fingers per hand. Where the Roman model (like most modern Japanese) has 4 plus 1 bead per decimal place, the standard suanpan has 5 plus 2 for less challenging arithmetic algorithms in a hexadecimal numeral system. Instead of running on wires as in the Chinese and Japanese models, the beads of Roman model run in groves, presumably making arithmetic calculations much slower.
Another possible source of the suanpan are the Chinese counting rods, which operated with a decimal system but lacked the concept of zero as a place holder. The zero was probably introduced to the Chinese in the Tang Dynasty (618-907) when travel in the Indian Ocean and the Middle East would have provided direct contact with India and Islam allowing them to acquire the concept of zero and the decimal point from Indian and Islamic merchants and mathematicians.
Korean and Japanese abacuses
The abacus migrated from China to Korea around the year 1400 and later Japan, around the year 1600.[12] Korea's version of the abacus is called jupan (주판) or supan (수판) or jusan (주산).
The Chinese suanpan was called soroban (算盤, そろばん, lit. "Counting tray") in Japan.[13] Like the suanpan, the soroban is still used in Japan today, even with the proliferation, practicality, and affordability of pocket electronic calculators.
Native American abacuses
Some sources mention the use of an abacus called a nepohualtzintzin in ancient Aztec culture. This Mesoamerican abacus used a 5-digit base-20 system.
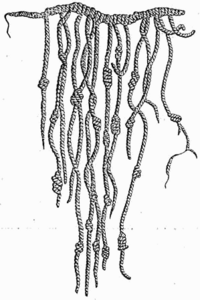
The quipu of the Incas was a system of knotted cords used to record numerical data, like advanced tally sticks—but not used to perform calculations. Calculations were carried out using a yupana (quechua for "counting tool"; see figure) which was still in use after the conquest of Peru. The working principle of a yupana is unknown, but in 2001 an explanation of the mathematical basis of these instruments was proposed. By comparing the form of several yupanas, researchers found that calculations were based using the Fibonacci sequence 1,1,2,3,5 and powers of 10, 20 and 40 as place values for the different fields in the instrument. Using the Fibonacci sequence would keep the number of grains within any one field at minimum.
Russian abacus
The Russian abacus, the schoty (счёты), usually has a single slanted deck, with ten beads on each wire (except one wire which has four beads, for quarter-ruble fractions). This wire is usually near the user. (Older models have another 4-bead wire for quarter-kopeks, which were minted until 1916.) The Russian abacus is often used vertically, with wires from left to right in the manner of a book. The wires are usually bowed to bulge upward in the center, in order to keep the beads pinned to either of the two sides. It is cleared when all the beads are moved to the right. During manipulation, beads are moved to the left. For easy viewing, the middle 2 beads on each wire (the 5th and 6th bead) usually have a colour different from the other 8 beads. Likewise, the left bead of the thousands wire (and the million wire, if present) may have a different color.
The Russian abacus is still in use today in shops and markets throughout the former Soviet Union, although it is no longer taught in most schools.
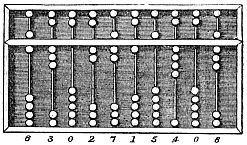
School abacus
Around the world, abaci have been used in pre-schools and elementary schools as an aid in teaching the numeral system and arithmetic. In Western countries, a bead frame similar to the Russian abacus but with straight wires and a vertical frame has been common (see image). It is still often seen as a plastic or wooden toy.
The type of abacus shown here is often used to represent numbers without the use of place value. Each bead and each wire has the same value and used in this way it can represent numbers up to 100.
The most significant educational advantage of using an abacus, rather than loose beads or counters, when practicing counting and simple addition is that it gives the student an awareness of the groupings of 10 which are the foundation of our number system. Although adults take this base 10 structure for granted, it is actually difficult to learn. Many 6-year-olds can count to 100 by rote with only a slight awareness of the patterns involved.
Uses by the blind
An adapted abacus, called a Cranmer abacus is still commonly used by individuals who are blind. A piece of soft fabric or rubber is placed behind the beads so that they do not move inadvertently. This keeps the beads in place while the users feel or manipulate them. They use an abacus to perform the mathematical functions multiplication, division, addition, subtraction, square root and cubic root.
Although blind students have benefited from talking calculators, the abacus is still very often taught to these students in early grades, both in public schools and state schools for the blind. The abacus teaches math skills that can never be replaced with talking calculators and is an important learning tool for blind students. Blind students also complete math assignments using a braille-writer and Nemeth code (a type of braille code for math) but large multiplication and long division problems can be long and difficult. The abacus gives blind and visually impaired students a tool to compute math problems that equals the speed and mathematical knowledge required by their sighted peers using pencil and paper. Many blind people find this number machine a very useful tool throughout life.
Abacuses in Medieval Pictures
Notes
- ↑ Edwin D. Reilly and William Leonard Langer, Concise Encyclopedia of Computer Science (New York: John Wiley and Sons, 2004), 825.
- ↑ 2.0 2.1 David Eugene Smith, History of Mathematics (Volume 2) (Courier Dover Publications, 1958, ISBN 0486204308), 159-160.
- ↑ Oxford English Dictionary, 1989.
- ↑ Merriam-Webster's 2003.
- ↑ Ettore Carruccio, Mathematics And Logic in History And in Contemporary Thought (Aldine Transaction, 2006, ISBN 0202308502), 14.
- ↑ Thomas Crump, The Japanese Numbers Game: The Use and Understanding of Numbers in Modern Japan (New York: Routledge, 1992), 188.
- ↑ J. M. Pullan, The History of the Abacus (London: Books That Matter, 1968), 18.
- ↑ Peter N. Stearns and William Leonard Langer, The Encyclopedia of World History: Ancient, Medieval, and Modern, Chronologically Arranged (New York: Houghton Mifflin Books, 2001), 44.
- ↑ Thomas William Körner and William Leonard Langer, The Pleasures of Counting (New York: Houghton Mifflin Books, 1996), 232.
- ↑ Richard Anthony Mollin, Fundamental Number Theory with Applications (CRC Press, 1998), 3.
- ↑ Peng Yoke Ho, Li, Qi and Shu: An Introduction to Science and Civilization in China (Courier Dover Publications, 2000), 71.
- ↑ abacus Retrieved December 21, 2017.
- ↑ The Abacus: A Brief History. Retrieved December 21, 2017.
ReferencesISBN links support NWE through referral fees
- Carruccio, Ettore. Mathematics And Logic in History And in Contemporary Thought. Aldine Transaction, 2006. ISBN 0202308502.
- Crump, Thomas. The Japanese Numbers Game: The Use and Understanding of Numbers in Modern Japan. Routledge, 1992. ISBN 0415056098.
- Domenici, Viviano and Davide Domenici. "Talking Knots of the Inka" Archaeology 49 (6) (November/December 1996)
- Kojima, Takashi. The Japanese Abacus: its Use and Theory. Tokyo; New York: Charles E. Tuttle, 1954. ISBN 0804802785.
- Körner, Thomas William, and William Leonard Langer. The Pleasures of Counting. Houghton Mifflin Books, 1996. ISBN 0521568234.
- Menninger, Karl W. Number Words and Number Symbols: A Cultural History of Numbers. MIT Press, 1969. ISBN 0262130408.
- Mollin, Richard Anthony. Fundamental Number Theory with Applications. CRC Press, 1998. ISBN 0849339871.
- Peng Yoke Ho. Li, Qi and Shu: An Introduction to Science and Civilization in China. Courier Dover Publications, 2000. ISBN 0486414450.
- Pullan, J. M. The History of the Abacus. London: Books That Matter, 1968. ISBN 0090894103.
- Reilly, Edwin D., and William Leonard Langer. Concise Encyclopedia of Computer Science. John Wiley and Sons, 2004. ISBN 0470090952.
- Smith, David Eugene. History of Mathematics. (Volume 2). Courier Dover Publications, 1958. ISBN 0486204308.
- Stearns, Peter N., and William Leonard Langer. The Encyclopedia of World History: Ancient, Medieval, and Modern, Chronologically Arranged. Houghton Mifflin Books, 2001. ISBN 0395652375.
External links
All links retrieved June 13, 2023.
- Abacus: Mystery of the Bead - an Abacus Manual
- Abacus in Various Number Systems
- History of the abacus and more
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.