Surface tension

Continuum mechanics

Conservation of mass Conservation of momentum Navier–Stokes equations Tensors Solid mechanics Solids · Stress · Deformation · Finite strain theory · Infinitesimal strain theory · Elasticity · Linear elasticity · Plasticity · Viscoelasticity · Hooke's law · Rheology Fluid mechanics Fluids · Fluid statics Fluid dynamics · Viscosity · Newtonian fluids Non-Newtonian fluids Surface tension Scientists Newton · Stokes · Navier · Cauchy· Hooke

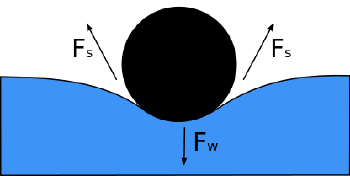
In physics, surface tension is an effect within the surface layer of a liquid that causes that layer to behave as an elastic sheet. This effect allows insects (such as the water strider) to walk on water. It allows small metal objects such as needles, razor blades, or foil fragments to float on the surface of water, and causes capillary action. Interface tension is the name of the same effect when it takes place between two liquids.

The cause of surface tension

Diagram of the forces on a molecule of liquid.

Surface tension is caused by the attraction between the molecules of the liquid by various intermolecular forces. In the bulk of the liquid each molecule is pulled equally in all directions by neighboring liquid molecules, resulting in a net force of zero. At the surface of the liquid, the molecules are pulled inwards by other molecules deeper inside the liquid but they are not attracted as intensely by the molecules in the neighboring medium (be it vacuum, air or another liquid). Therefore, all of the molecules at the surface are subject to an inward force of molecular attraction which can be balanced only by the resistance of the liquid to compression. Thus, the liquid squeezes itself together until it has the locally lowest surface area possible.

Another way to think about it is that a molecule in contact with a neighbor is in a lower state of energy than if it weren't in contact with a neighbor. The interior molecules all have as many neighbors as they can possibly have. But the boundary molecules have fewer neighbors than interior molecules and are therefore in a higher state of energy. For the liquid to minimize its energy state, it must minimize its number of boundary molecules and therefore minimize its surface area.

As a result of this minimizing of surface area, the surface will want to assume the smoothest flattest shape it can (rigorous proof that "smooth" shapes minimize surface area relies on use of the Euler-Lagrange Equation). Since any curvature in the surface shape results in higher area, a higher energy will also result. Consequently, the surface will push back on the disturbing object in much the same way a ball pushed uphill will push back to minimize its gravitational energy.

Surface tension in everyday life

Water beading on a leaf

Water drop animation

Some examples of the effects of surface tension seen with ordinary water:

• Beading of rain water on the surface of a waxed automobile. Water adheres weakly to wax and strongly to itself, so water clusters in drops. Surface tension gives them their near-spherical shape, because a sphere has the smallest possible surface area to volume ratio.

• Formation of drops occurs when a mass of liquid is stretched. The animation shows water adhering to the faucet gaining mass until it is stretched to a point where the surface tension can no longer bind it to the faucet. It then separates and surface tension forms the drop into a sphere. If a stream of water were running from the faucet, the stream would break up into drops during its fall. This is because of gravity stretching the stream, and surface tension then pinching it into spheres.

Surface tension has a big influence on other common phenomena, especially when certain substances, surfactants, are used to decrease it:

• Soap Bubbles have very large surface areas for very small masses. Bubbles cannot be formed from pure water because water has very high surface tension, but the use of surfactants can reduce the surface tension more than tenfold, making it very easy to increase its surface area.
• Colloids are a type of solution where surface tension is also very important. Oil will not spontaneously mix with water, but the presence of a surfactant provides a decrease in surface tension that allows the formation of small droplets of oil in the bulk of water (or vice versa).

Physics definition of surface tension

Diagram shows, in crossection, a needle floating on the surface of water. Cross-section of a needle floating on the surface of water. Fw is the weight and Fs are surface tension resultant forces.

Surface tension is represented by the symbol σ, γ or T and is defined as the force along a line of unit length where the force is parallel to the surface but perpendicular to the line. One way to picture this is to imagine a flat soap film bounded on one side by a taut thread of length, L. The thread will be pulled toward the interior of the film by a force equal to γL. Surface tension is therefore measured in newtons per meter (N·m^-1), although the cgs unit of dynes per cm is normally used.

A better definition of surface tension, in order to treat its thermodynamics, is work done per unit area. As such, in order to increase the surface area of a mass of liquid an amount, δA, a quantity of work, γδA, is needed. Since mechanical systems try to find a state of minimum potential energy, a free droplet of liquid naturally assumes a spherical shape. This is because a sphere has the minimum surface area for a given volume. Therefore surface tension can be also measured in joules per square meter (J·m^-2), or, in the cgs system, ergs per cm².

The equivalence of both units can be proven by dimensional analysis.

A related quantity is the energy of cohesion, which is the energy released when two bodies of the same liquid become joined by a boundary of unit area. Since this process involves the removal of a unit area of surface from each of the two bodies of liquid, the energy of cohesion is equal to twice the surface energy. A similar concept, the energy of adhesion, applies to two bodies of different liquids. Energy of adhesion is linked to the surface tension of an interface between two liquids. $\scriptstyle W_{adh}\ =\ W_{coh}^{\alpha }+W_{coh}^{\beta }-\gamma _{\alpha }^{\beta }$

See also Cassie's law.

Water strider physics

Water striders using water surface tension when mating.

The photograph shows water striders standing on the surface of a pond. It is clearly visible that its feet cause indentations in the water's surface. And it is intuitively evident that the surface with indentations has more surface area than a flat surface. If surface tension tends to minimize surface area, how is it that the water striders are increasing the surface area?

Recall that what nature really tries to minimize is potential energy. By increasing the surface area of the water, the water striders have increased the potential energy of that surface. But note also that the water striders' center of mass is lower than it would be if they were standing on a flat surface. So their potential energy is decreased. Indeed when you combine the two effects, the net potential energy is minimized. If the water striders depressed the surface any more, the increased surface energy would more than cancel the decreased energy of lowering the insects' center of mass. If they depressed the surface any less, their higher center of mass would more than cancel the reduction in surface energy.

The photo of the water striders also illustrates the notion of surface tension being like having an elastic film over the surface of the liquid. In the surface depressions at their feet it is easy to see that the reaction of that imagined elastic film is exactly countering the weight of the insects.

Liquid in a vertical tube

Diagram of a Mercury Barometer

An old style mercury barometer consists of a vertical glass tube about 1 cm in diameter partially filled with mercury, and with a vacuum in the unfilled volume (see diagram to the right). Notice that the mercury level at the center of the tube is higher than at the edges, making the upper surface of the mercury dome-shaped. The center of mass of the entire column of mercury would be slightly lower if the top surface of the mercury were flat over the entire cross-section of the tube. But the dome-shaped top gives slightly less surface area to the entire mass of mercury. Again the two effects combine to minimize the total potential energy. Such a surface shape is known as a convex meniscus.

The reason people consider the surface area of the entire mass of mercury, including the part of the surface that is in contact with the glass, is because mercury does not adhere at all to glass. So the surface tension of the mercury acts over its entire surface area, including where it is in contact with the glass. If instead of glass, the tube were made out of copper, the situation would be very different. Mercury aggressively adheres to copper. So in a copper tube, the level of mercury at the center of the tube will be lower rather than higher than at the edges (that is, it would be a concave meniscus). In a situation where the liquid adheres to the walls of its container, we consider the part of the fluid's surface area that is in contact with the container to have negative surface tension. The fluid then works to maximize the contact surface area. So in this case increasing the area in contact with the container decreases rather than increases the potential energy. That decrease is enough to compensate for the increased potential energy associated with lifting the fluid near the walls of the container.

Surface tension prevents this flower from sinking

The angle of contact of the surface of the liquid with the wall of the container can be used to determine the surface tension of the liquid-solid interface provided that the surface tension of the liquid-air interface is known. The relationship is given by:

$\gamma _{\mathrm {ls} }\ =\ -\gamma _{\mathrm {la} }\cos \theta$

where

• $\scriptstyle \gamma _{\mathrm {ls} }$ is the liquid-solid surface tension,
• $\scriptstyle \gamma _{\mathrm {la} }$ is the liquid-air surface tension,
• $\scriptstyle \theta$ is the contact angle, where a concave meniscus has contact angle less than 90° and a convex meniscus has contact angle of greater than 90°.

If a tube is sufficiently narrow and the liquid adhesion to its walls is sufficiently strong, surface tension can draw liquid up the tube in a phenomenon known as capillary action. The height the column is lifted to is given by:

$h\ =\ {\frac {2\gamma _{\mathrm {la} }\cos \theta }{\rho gr}}$

where

• $\scriptstyle h$ is the height the liquid is lifted,
• $\scriptstyle \gamma _{\mathrm {la} }$ is the liquid-air surface tension,
• $\scriptstyle \rho$ is the density of the liquid,
• $\scriptstyle r$ is the radius of the capillary,
• $\scriptstyle g$ is the acceleration of gravity,
• $\scriptstyle \theta$ is the angle of contact described above. Note that if $\scriptstyle \theta$ is greater than 90°, as with mercury in a glass container, the liquid will be depressed rather than lifted.

Pool of liquid on a nonadhesive surface

Pouring mercury onto a horizontal flat sheet of glass results in a puddle that has a perceptible thickness (do not try this except under a fume hood. Mercury vapor is a toxic hazard). The puddle will spread out only to the point where it is a little under half a centimeter thick, and no thinner. Again this is due to the action of mercury's strong surface tension. The liquid mass flattens out because that brings as much of the mercury to as low a level as possible. But the surface tension, at the same time, is acting to reduce the total surface area. The result is the compromise of a puddle of a nearly fixed thickness.

The same surface tension demonstration can be done with water, but only on a surface made of a substance that the water does not adhere to. Wax is such a substance. Water poured onto a smooth, flat, horizontal wax surface, say a waxed sheet of glass, will behave similarly to the mercury poured onto glass.

The thickness of a puddle of liquid on a nonadhesive horizontal surface is given by

$h\ =\ 2{\sqrt {\frac {\gamma }{g\rho }}}$

where

$\scriptstyle h$ is the depth of the puddle in centimeters or meters.

$\scriptstyle \gamma$ is the surface tension of the liquid in dynes per centimeter or newtons per meter.

$\scriptstyle g$ is the acceleration due to gravity and is equal to 980 cm/s2 or 9.8 m/s2

$\scriptstyle \rho$ is the density of the liquid in grams per cubic centimeter or kilograms per cubic meter

For mercury, $\scriptstyle \gamma _{\mathrm {Hg} }\ =\ 487\ \mathrm {\frac {dyn}{cm}}$ and $\scriptstyle \rho _{\mathrm {Hg} }\ =\ 13.5\ \mathrm {\frac {g}{cm^{3}}}$, which gives $\scriptstyle h_{\mathrm {Hg} }\ =\ 0.38\ \mathrm {cm}$. For water at 25 °C, $\scriptstyle \gamma _{\mathrm {H_{2}O} }\ =\ 72\ \mathrm {\frac {dyn}{cm}}$ and $\scriptstyle \rho _{\mathrm {H_{2}O} }\ =1.0\ \mathrm {\frac {g}{cm^{3}}}$, which gives $\scriptstyle h_{\mathrm {H_{2}O} }\ =\ 0.54\ \mathrm {cm}$.

In reality, the thicknesses of the puddles will be slightly less than these calculated values. This is due to the fact that surface tension of the mercury-glass interface is slightly less than that of the mercury-air interface. Likewise, the surface tension of the water-wax interface is less than that of the water-air interface. The contact angle, as described in the previous subsection, determines by how much the puddle thickness is reduced from the theoretical.

Liquid surfaces as minimization solver

To find the shape of the minimal surface bounded by some arbitrary shaped frame using strictly mathematical means can be a daunting task. Yet by fashioning the frame out of wire and dipping it in soap-solution, an approximately minimal surface will appear in the resulting soap-film within seconds. Without a single calculation, the soap-film arrives at a solution to a complex minimization equation on its own.

Measuring methods

• Du Noüy Ring method: The traditional method used to measure surface or interfacial tension. Wetting properties of the surface or interface have little influence on this measuring technique. Maximum pull exerted on the ring by the surface is measured.

• Wilhelmy plate method: A universal method especially suited to check surface tension over long time intervals. A vertical plate of known perimeter is attached to a balance, and the force due to wetting is measured.

• Spinning drop method: This technique is ideal for measuring low interfacial tensions. The diameter of a drop within a heavy phase is measured while both are rotated.

• Pendant drop method: Surface and interfacial tension can be measured by this technique, even at elevated temperatures and pressures. Geometry of a drop is analyzed optically.

Surface Tension can be measured using the pendant drop method on a ramé-hart goniometer.

• Bubble pressure method (Jaeger's method): A measurement technique for determining surface tension at short surface ages. Maximum pressure of each bubble is measured.

• Drop volume method: A method for determining interfacial tension as a function of interface age. Liquid of one density is pumped into a second liquid of a different density and time between drops produced is measured.

• Capillary rise method: The end of a capillary is immersed into the solution. The height at which the solution reaches inside the capillary is related to the surface tension by the previously discussed equation.

• Stalagmometric method: A method of weighting and reading a drop of liquid.

Surface tension and thermodynamics

Thermodynamic definition

As stated above, the mechanical work needed to increase a surface is $\scriptstyle dW=\gamma dA$. For a reversible process, $\scriptstyle dG=VdP+\gamma dA-SdT$, therefore at constant temperature and pressure, surface tension equals Gibbs free energy per surface area:

$\gamma =\left({\frac {\partial G}{\partial A}}\right)_{P,T}$, where $\scriptstyle G$ is Gibbs free energy and $\scriptstyle A$ is the area.

Influence of temperature on surface tension

Temperature dependency of the surface tension of benzene

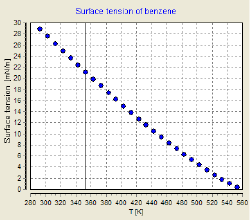
Surface tension depends on temperature; for that reason, when a value is given for the surface tension of an interface, temperature must be explicitly stated. The general trend is that surface tension decreases with the increase of temperature, reaching a value of 0 at the critical temperature. There are only empirical equations to relate surface tension and temperature.

Influence of solute concentration on surface tension

Solutes can have different effects on surface tension depending on their structure:

• No effect, for example sugar
• Increase of surface tension, inorganic salts
• Decrease surface tension progressively, alcohols
• Decrease surface tension and, once a minimum is reached, no more effect: Surfactants

Pressure jump across a curved surface

If viscous forces are absent, the pressure jump across a curved surface is given by the Young-Laplace Equation, which relates pressure inside a liquid with the pressure outside it, the surface tension and the geometry of the surface.

$\Delta P=\gamma {\frac {dA}{dV}}$.

This equation can be applied to any surface:

• For a flat surface $\scriptstyle {\frac {dA}{dV}}\ =\ 0$ so the pressure inside is the same as the pressure outside.
• For a spherical surface $\scriptstyle P_{I}\ =\ P_{O}+{\frac {2\gamma }{R}}$
• For a toroidal surface $\scriptstyle P_{I}\ =\ P_{O}+\gamma \left({\frac {1}{R}}+{\frac {1}{r}}\right)$, where r and R are the radii of the toroid.

The table shows an example of how the pressure increases, showing that for not very small drops the effect is subtle but the pressure difference becomes enormous when the drop sizes approach the molecular size (a drop with a 1 nm radius contains approximately 100 water molecules), this can be attributed to the fact that at a very small scale the laws of continuum physics cannot be applied anymore.

ΔP for water drops of different radii at STP
Droplet radius	1 mm	0.1 mm	1 μm	10 nm
ΔP (atm)	0.0014	0.0144	1.436	143.6

Influence of particle size on vapor pressure

Starting from Clausius-Clapeyron relation Kelvin Equation II can be obtained; it explains that because of surface tension, vapor pressure for small droplets of liquid in suspension is greater than standard vapor pressure of that same liquid when the interface is flat. That is to say that when a liquid is forming small droplets, the concentration of vapor of that liquid in the surroundings is greater, this is due to the fact that the pressure inside the droplet is greater than outside.

$P_{v}^{fog}=P_{v}^{o}e^{\frac {V2\gamma }{RTr_{k}}}$

$\scriptstyle P_{v}^{o}$ is the standard vapor pressure for that liquid at that temperature and pressure.

$\scriptstyle V$ is the molar volume.

$\scriptstyle R$ is the gas constant

$r_{k}$ is the Kelvin radius, the radius of the droplets.

This equation is used in catalyst chemistry to assess mesoporosity for solids.

The table shows some calculated values of this effect for water at different drop sizes:

P/P0 for water drops of different radii at STP
Droplet radius (nm)	1000	100	10	1
P/P0	1.0011	1.0106	1.1115	2.8778

The effect becomes clear for very low drop sizes, as a drop on 1 nm radius has about 100 molecules inside, which is a quantity small enough to require a quantum mechanics analysis.

Surface tension values

Surface tension values for some interfaces
Interface	Temperature	γ in (mN·m–1)
Water - air	20º C	72.86±0.05
Water - air	21.5º C	72.75
Water - air	25º C	71.99±0.05
Methylene iodide - air	20º C	67.00
Methylene iodide - air	21.5º C	63.11
Ethylene glycol - air	25º C	47.3
Ethylene glycol - air	40º C	46.3
Dimethyl sulfoxide - air	20º C	43.54
Propylene carbonate - air	20º C	41.1
Benzene - air	20º C	28.88
Benzene - air	30º C	27.56
Toluene - air	20º C	28.52
Chloroform - air	25º C	26.67
Propionic acid - air	20º C	26.69
Butyric acid - air	20º C	26.51
Carbon tetrachloride - air	25º C	26.43
Butyl acetate - air	20º C	25.09
Diethylene Glycol - air	20º C	30.09
Nonane - air	20º C	22.85
Methanol - air	20º C	22.50
Ethanol - air	20º C	22.39
Ethanol - air	30º C	21.55
Octane - air	20º C	21.62
Heptane - air	20º C	20.14
Ether - air	25º C	20.14
Mercury - air	20º C	486.5
Mercury - air	25º C	485.5
Mercury - air	30º C	484.5
NaCl - air	1073º C	115
KClO3 - air	20º C	81
Water - 1-Butanol	20º C	1.8
Water - Ethyl acetate	20º C	6.8
Water - Heptanoic acid	20º C	7.0
Water - Benzaldehyde	20º C	15.5
Water - Mercury	20º C	415
Ethanol - Mercury	20º C	389

Surface tension values for some interfaces at the indicated temperatures. Note that the SI units millinewtons per meter (mN·m^–1) are equivalent to the cgs units, dynes per centimeter (dyn·cm^–1).

See also

• Contact angle, the angle the surface makes with the wall of a container.
• Cheerios effect, the tendency for small wettable floating objects to attract one another
• Water striders, insects that rely on the surface tension of water to walk on top of it
• Wetting and dewetting
• Meniscus, surface curvature formed by a liquid in a container
• Tolman length, leading term in correcting the surface tension for curved surfaces
• Surfactants, substances which reduce surface tension
• Eötvös rule, a rule for predicting surface tension dependent on temperature
• The Dortmund Data Bank contains experimental temperature-dependent surface tensions

References

ISBN links support NWE through referral fees

• Adamson, Arthur W., and Alice P. Gast. Physical Chemistry of Surfaces, 6th ed. New York: John Wiley, 1997. ISBN 0471148733.
• Lamb, Sir Horace. Hydrodynamics, 6th ed. Dover, 1932.
• Savino, Raffaele. Surface Tension-Driven Flows and Applications. Research Signpost, 2006. ISBN 8130800659.
• Sears, Francis Weston, and Mark W. Zemanski. University Physics, 2nd ed. Addison Wesley, 1955.
• Venables, John A. Introduction to Surface and Thin Film Processes. Cambridge, UK: Cambridge University Press, 2000. ISBN 0521785006.
• White, Harvey E. Modern College Physics. van Nostrand, 1948.
• Zangwill, Andrew. Physics at Surfaces. Cambridge, UK: Cambridge University Press, 2001. ISBN 0521347521.

External links

All links retrieved February 26, 2023.

• On surface tension and interesting real-world cases
• Surface tension values of some common test liquids for surface energy analysis

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Surface_tension  ^history
• Surface_tension_values  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Surface tension"

Note: Some restrictions may apply to use of individual images which are separately licensed.