Spring (device)

Helical or coil springs designed for tension.

A spring is a flexible, elastic device used to store mechanical energy. When a force is applied to a spring, it expands or contracts to a certain extent, and when the force is released, the spring attempts to return to its earlier state.

Springs can be made of a variety of elastic materials, including fluids, but springs used in mechanical devices are generally made of metal. They also vary in shape; familiar shapes being helical, spiral, and flat.

Based on their behavior, springs are used to move objects, absorb vibrations, and control mechanical shock. For instance, they are useful in clocks, shock absorbers, motorized toys, pogo sticks, automobile engine valves, and door-closing mechanisms. Technically, a wooden bow is a form of spring.

Historical appearance

Simple, non-coiled springs, such as the bow (used with an arrow), have been used through much of human history. In the Bronze Age, more sophisticated spring devices were used, as indicated by the spread of tweezers in many cultures. Ctesibius of Alexandria developed a method for making bronze with spring-like characteristics by producing an alloy of bronze with an increased proportion of tin, then hardening it by hammering after it was cast.

Coiled springs appeared early in the fifteenth century, leading to the development of the first spring-powered clocks in that century. By the sixteenth century, the first large, spring-powered watches were produced.

Materials used for springs

As noted above, various elastic materials can be used to make springs. Even fluids under pressure demonstrate spring-like properties. Most springs, however, are made of metal, particularly hardened steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication. Some non-ferrous metals are also used, including phosphor bronze for parts requiring corrosion resistance, and beryllium copper for springs carrying electrical current (because its electrical resistance is low).

Types of springs

A spiral hair spring.

Springs are classified according their properties.

Depending on the load, they may be classified as:

• Tension/Extension spring
• Compression spring
• Torsional spring

In the case of tension/extension springs and compression springs, there is axial load. On the other hand, the torsional spring has torsional force.

Depending on the material of the spring, it can be classified as:

• Wire/Coil spring
• Flat spring

The most common types of spring are:

• Cantilever spring - a spring that is fixed at only one end.
• Coil spring or helical spring - a spring (made by winding a wire around a cylinder) and the conical spring - these are types of torsion spring, because the wire itself is twisted when the spring is compressed or stretched. These are in turn of two types:
  • Compression springs are designed to become shorter when loaded. Their turns are not touching in the unloaded position, and they need no attachment points.
    • A volute spring is a compression spring in the form of a cone, designed so that under compression the coils are not forced against each other, thus permitting longer travel.
  • Tension or extension springs are designed to become longer under load. Their turns are normally touching in the unloaded position, and they have a hook, eye or some other means of attachment at each end.
• Hairspring or balance spring - a delicate spiral torsion spring used in watches, galvanometers, and places where electricity must be carried to partially-rotating devices such as steering wheels without hindering the rotation.
• Leaf spring - a flat springy sheet, used in vehicle suspensions, electrical switches, bows.
• V-spring - used in antique firearm mechanisms such as the wheellock, flintlock and percussion cap locks.

Other types include:

• Belleville washer or Belleville spring - a disc-shaped spring commonly used to apply tension to a bolt (and in the initiation mechanism of pressure-activated landmines).
• Constant-force spring - a tightly rolled ribbon that exerts a nearly constant force as it is unrolled.
• Gas spring - a volume of compressed gas.
• Ideal Spring - the notional spring used in physics: it has no weight, mass, or damping losses.
• Mainspring - a spiral ribbon shaped spring used as a power source in watches, clocks, music boxes, windup toys, and mechanically powered flashlights
• Rubber band - a tension spring where energy is stored by stretching the material.
• Spring washer - used to apply a constant tensile force along the axis of a fastener.
• Torsion spring - any spring designed to be twisted rather than compressed or extended. Used in torsion bar vehicle suspension systems.
• Negator spring - a thin metal band slightly concave in cross-section. When coiled it adopts a flat cross-section but when unrolled it returns to its former curve, thus producing a constant force throughout the displacement and negating any tendency to re-wind. The commonest application is the retracting steel tape rule.
• Wave spring - a thin spring-washer into which waves have been pressed.

Theory

Two springs attached to a wall and a mass. In a situation like this, the two springs can be replaced by one with a spring constant of k_eq=k₁+k₂.

In classical physics, a spring can be thought of as a device that absorbs potential energy when it is extended or compressed. The extension or compression strains the bonds between the atoms of the elastic material.

Hooke's Law

If the spring undergoes only slight stretching or compression, it obeys Hooke's law of elasticity. This law was named after British physicist Robert Hooke, who discovered the principle in 1676.

In simple terms, Hooke's law states that the force with which a spring pushes back toward its equilibrium position is linearly proportional to the distance from its equilibrium length. More precisely, Hooke's law states that the extension of an elastic rod (its distended length minus its relaxed length) is linearly proportional to its tension, the force used to stretch it. Likewise, the contraction (negative extension) is proportional to the compression (negative tension).

This law is valid only approximately, and only when the deformation (extension or contraction) is small compared to the spring's overall length. For deformations beyond the elastic limit, atomic bonds get broken or rearranged, and a spring may snap, buckle, or become permanently deformed. Many materials have no clearly defined elastic limit, and Hooke's law cannot be meaningfully applied to these materials.

In mathematical terms, Hooke's law can be written as:

$F=-kx,\$

where

x is the distance through which the spring has been elongated or compressed,

F is the restoring force exerted by the spring, and

k is the spring constant or force constant of the spring.

Simple harmonic motion

Given that force (F) is equal to mass (m) times acceleration, a, the force equation can be written as:

$F=-kx=ma.\,$

The displacement, x, as a function of time. The amount of time that passes between peaks is called the period.

Given that acceleration is the second time derivative of x, one can write:

$-kx=m{\frac {d^{2}x}{dt^{2}}}.\,$

Rearranging the results, one gets the following differential equation:

${\frac {d^{2}x}{dt^{2}}}+{\frac {k}{m}}x=0\,$

The solution of this equation is the sum of a sine and a cosine:

$x(t)=A\sin \left(t{\sqrt {\frac {k}{m}}}\right)+B\cos \left(t{\sqrt {\frac {k}{m}}}\right).\,$

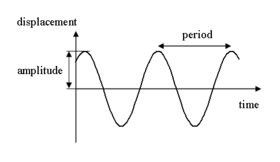
The graph of this function is displayed in the image on the right.

Zero-length springs

"Zero-length spring" is the standard term for a spring that exerts zero force when it has zero length. In practice, a spring with "negative" length (in which the coils press together when the spring is relaxed) is combined with an extra length of inelastic material.

This type of spring was developed in 1932 by Lucien LaCoste for use in a vertical seismograph. A spring with zero length can be attached to a mass on a hinged boom, such that the force on the mass is almost exactly balanced by the vertical component of the force from the spring, whatever the position of the boom. This creates a pendulum with a very long period. Long-period pendulums enable seismometers to sense the slowest waves from earthquakes. The LaCoste suspension with zero-length springs is also used in gravimeters because it is very sensitive to changes in gravity.

Springs for closing doors are often made to have roughly zero length so that they will exert force even when the door is almost closed, allowing the door to close firmly.

References

ISBN links support NWE through referral fees

• Associated Spring Corporation. 1964. Handbook of Mechanical Spring Design. Bristol, CT: Associated Spring Corp. ASIN: B000TRJQEU.

• Brown, A. A. D. 1981. Mechanical Springs. Engineering Design Guides, 42. [S.l.]: Published for the Design Council, the British Standards Institution, and the Council of Engineering Institutions by Oxford University Press. ISBN 0198591810.

• Dohrn-van Rossum, Gerhard. 1997. History of the Hour: Clocks and Modern Temporal Orders. Chicago: Univ. of Chicago Press. ISBN 0226155102.

• Usher, Abbott Payson. 1988. A History of Mechanical Inventions. New York: Dover. ISBN 048625593X.

• Wahl, A. M. 1963. Mechanical Springs. New York: McGraw-Hill. OCLC 562873.

External links

All links retrieved February 8, 2023.

• Springs. How Products Are Made.
• Spring Terminology

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Spring_(device)  ^history
• Spring_(device)  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Spring (device)"

Note: Some restrictions may apply to use of individual images which are separately licensed.