Resistivity

A piece of resistive material with electrical contacts on both ends.

Electrical resistivity (also known as specific electrical resistance) is a measure of how strongly a material opposes the flow of electric current. A low value of resistivity indicates a material that readily allows the movement of electrical charge. The SI unit of electrical resistivity is the ohm meter (Ω-m). Knowledge of the resistivity of various materials is useful for the choice of materials needed for manufacturing electrical and electronic components.

Definitions

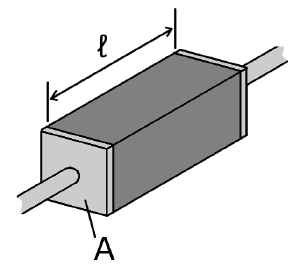
The electrical resistivity ρ (rho) of a material is given by

$\rho ={\frac {RA}{\ell }}$

where

ρ is the static resistivity (measured in ohm meters, Ω-m);

R is the electrical resistance of a uniform specimen of the material (measured in ohms, Ω);

$\ell$ is the length of the piece of material (measured in meters, m);

A is the cross-sectional area of the specimen (measured in square meters, m²).

Electrical resistivity can also be defined as

$\rho ={E \over J}$

where

E is the magnitude of the electric field (measured in volts per meter, V/m);

J is the magnitude of the current density (measured in amperes per square meter, A/m²).

Finally, electrical resistivity is also defined as the inverse of the conductivity σ (sigma), of the material, or

$\rho ={1 \over \sigma }.$

Table of resistivities

This table shows the resistivity and temperature coefficient of various materials at 20 °C (68 °F)

Material	Resistivity (Ω-m) at 20 °C	Coefficient*	Reference
Silver	1.59×10−8	.0038
Copper	1.72×10−8	.0039
Gold	2.44×10−8	.0034
Aluminium	2.82×10−8	.0039
Calcium	3.3x10-8
Tungsten	5.60×10−8	.0045
Nickel	6.99×10−8	?
Iron	1.0×10−7	.005
Tin	1.09×10−7	.0045
Platinum	1.1×10−7	.00392
Lead	2.2×10−7	.0039
Manganin	4.82×10−7	.000002
Constantan	4.9×10−7	0.00001
Mercury	9.8×10−7	.0009
Nichrome	1.10×10−6	.0004
Carbon	3.5×10−5	-.0005
Germanium	4.6×10−1	-.048
Silicon	6.40×102	-.075
Glass	1010 to 1014	?
Hard rubber	approx. 1013	?
Sulfur	1015	?
Paraffin	1017	?
Quartz (fused)	7.5×1017	?
PET	1020	?
Teflon	1022 to 1024	?

*The numbers in this column increase or decrease the significand portion of the resistivity. For example, at 30°C (303.15 K), the resistivity of silver is 1.65×10⁻⁸. This is calculated as Δρ = α ΔT ρ_o where ρ_o is the resistivity at 20°C and α is the temperature coefficient

Temperature dependence

In general, electrical resistivity of metals increases with temperature, while the resistivity of semiconductors decreases with increasing temperature. In both cases, electron-phonon interactions can play a key role. At high temperatures, the resistance of a metal increases linearly with temperature. As the temperature of a metal is reduced, the temperature dependence of resistivity follows a power law function of temperature. Mathematically the temperature dependence of the resistivity ρ of a metal is given by the Bloch–Grüneisen formula:

$\rho (T)=\rho (0)+A\left({\frac {T}{\Theta _{R}}}\right)^{n}\int _{0}^{\frac {\Theta _{R}}{T}}{\frac {x^{n}}{(e^{x}-1)(1-e^{-x})}}dx$

where $\rho (0)$ is the residual resistivity due to defect scattering, A is a constant that depends on the velocity of electrons at the fermi surface, the Debye radius and the number density of electrons in the metal. $\Theta _{R}$ is the Debye temperature as obtained from resistivity measurements and matches very closely with the values of Debye temperature obtained from specific heat measurements. n is an integer that depends upon the nature of interaction:

1. n=5 implies that the resistance is due to scattering of electrons by phonons (as it is for simple metals)
2. n=3 implies that the resistance is due to s-d electron scattering (as is the case for transition metals)
3. n=2 implies that the resistance is due to electron-electron interaction.

As the temperature of the metal is sufficiently reduced (so as to 'freeze' all the phonons), the resistivity usually reaches a constant value, known as the residual resistivity. This value depends not only on the type of metal, but on its purity and thermal history. The value of the residual resistivity of a metal is decided by its impurity concentration. Some materials lose all electrical resistivity at sufficiently low temperatures, due to an effect known as superconductivity.

An even better approximation of the temperature dependence of the resistivity of a semiconductor is given by the Steinhart–Hart equation:

$1/T=A+B\ln(\rho )+C(\ln(\rho ))^{3}\,$

where A, B and C are the so-called Steinhart–Hart coefficients.

This equation is used to calibrate thermistors.

In non-crystalline semi-conductors, conduction can occur by charges quantum tunnelling from one localized site to another. This is known as variable range hopping and has the characteristic form of $\rho =Ae^{T^{-1/n}}$, where n=2,3,4 depending on the dimensionality of the system.

Complex resistivity

When analyzing the response of materials to alternating electric fields, as is done in certain types of tomography, it is necessary to replace resistivity with a complex quantity called impedivity (analogous to electrical impedance). Impedivity is the sum of a real component, the resistivity, and an imaginary component, the reactivity (analogous to reactance).

Resistivity density products

In some applications where the weight of an item is very important, resistivity density products are more important than absolute low resistance. It is often possible to make the conductor thicker, to make up for a higher resistivity; and in that case, a low resistivity density product material (or equivalently a high conductance to density ratio) is desirable.

This knowledge is useful for long-distance overhead powerline transmission. Aluminum is used rather than copper because it is lighter for the same conductance. Calcium, while theoretically better, is rarely if ever used, due to its highly reactive nature.

Material	Resistivity (nΩ•m)	Density (g/cm^3)	Resistivity - density product (nΩ•m•g/cm^3)
Calcium	33.6	1.55	52
Aluminum	26.50	2.70	72
Copper	16.78	8.96	150
Silver	15.87	10.49	166

See also

• Electricity
• Electronics
• Resistor

References

ISBN links support NWE through referral fees

• Dyos, G. T., and T. Farrell. 1992. Electrical Resistivity Handbook. IEE Materials & Devices Series, 10. London, UK: Peter Peregrinus, for the Institution of Electrical Engineers. ISBN 0863412661
• Giancoli, Douglas. 2007. Physics for Scientists and Engineers, with Modern Physics (Chapters 1-37), 4th ed. Mastering Physics Series. Upper Saddle River, NJ: Prentice Hall. ISBN 978-0136139263
• Plonus, Martin. 2001. Electronics and Communications for Scientists and Engineers. San Diego: Harcourt/Academic Press. ISBN 0125330847
• Rossiter, Paul L. 1991. The Electrical Resistivity of Metals and Alloys. Cambridge Solid State Science Series. Cambridge, UK: Cambridge University Press. ISBN 0521408725
• Tipler, Paul Allen, and Gene Mosca. 2004. Physics for Scientists and Engineers, Volume 2: Electricity and Magnetism, Light, Modern Physics, 5th ed. New York: W.H. Freeman. ISBN 0716708108

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Resistivity  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Resistivity"

Note: Some restrictions may apply to use of individual images which are separately licensed.