Quark
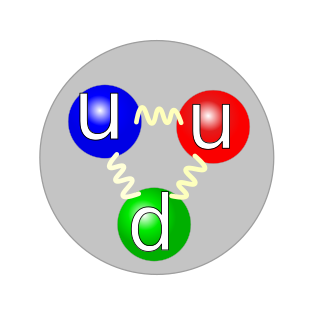
In particle physics, a quark is one of the elementary (or fundamental) particles that are the building blocks of matter. Elementary particles are classified as fermions and bosons, and fermions are subdivided into quarks and leptons. Quarks are fermions that experience the strong interaction (or strong nuclear force), which involves coupling with the bosons known as gluons. In other words, quarks couple with gluons to form composite particles such as protons and neutrons. By comparison, a lepton is a fermion that does not experience the strong interaction and does not couple with gluons.
Leptons and quarks come in pairs, and in three generations. Everyday matter is composed of the first generation: Two leptons, the electron and electron-neutrino; and two quarks, called Up and Down.
As is the case for all fundamental particles, the quark is a unified entity of wave and particle, which is known as the "wave-particle duality" of quantum physics. The particle aspect of the quark is point-like even at scales thousands of times smaller than the proton size. The wave aspect of the quark extends over the size of the atomic nucleus. The usual convention is to refer to such unified wave-particle fundamental entities as just "particles."
Etymology
The word "quark" was coined by Murray Gell-Mann as a nonsense word rhyming with "pork" (Gribbin 1998). Later, he found the same word in James Joyce's book Finnegans Wake, where seabirds give "three quarks," akin to three cheers. Joyce may have used the term to imitate a seabird call (like "quack" for ducks), as well as to make a pun on the relationship between Munster and its provincial capital, Cork, in the passage "Three quarks for Muster Mark! / Sure he has not got much of a bark / And sure any he has it's all beside the mark."
Quantum spin and probability
All particles (fundamental and composite) can be placed in one of two classes, distinguished by their quantum spin and the type of quantum probability statistics they obey: Fermi-Dirac probability or Bose-Einstein probability, neither of which is like classical probability. (A rough illustration of the difference is that the probability of two classical coins coming up the same is 50 percent, while for two fermion coins it is 0 percent and for two boson coins it is 100 percent.)
Both the quark and the electron are fermions with quantum spin -½, giving them the odd property of having to be rotated 720° in order to get back to where you started. (A familiar example of this sort of behavior is the Moebius Strip.) As far as everyday matter is concerned, these two types of fermions are essentially "eternal" and can be considered the "pixels of matter" out of which the physical world is constructed. The photon and gluon are bosons with quantum spin -1; they take only the usual 360° to return to the start. The bosons are ephemeral and "couple" the fundamental interactions of the fermions; they can be considered the "pixels of force" that hold all the fermions together as matter.
It is thought that during the first moments of Creation the temperature was so high that quarks could fly free, just like the electron can today. However, in all conditions found in the current universeâeven in supernovaeâthere are no isolated, free quarks; they are confined by their color charge into colorless combinations of pairs or triplets. All such combinations of quarks are given the generic term hadron. The electron, by contrast, is a lepton.
The quark hadrons are further subdivided into two classes. There are the fermion "pixels of matter" composed of three quarks, the baryons such as the protons and neutrons. Then there are the boson "pixels of force" composed of a quark-antiquark pair, the mesons such as the pions that bind the atomic nucleus together.
The fundamental fermions come in three generations. (The bosons do not.) The quarks and electrons that make up regular matter are all members of the first generation. In this generation, there are two "flavors" of quark, the U- and D-quark (or Up and Down quarks), and two flavors of lepton, the electron and the neutrino. A proton is composed of one D- and two U-quarks; the neutron is one U- and two D-quarks.
In the second generation of fundamental fermions, the pattern is repeated, the only difference being that the particles are much more massive that their first generation counterparts; otherwise they are identical. There are the two quarks, the S- and C-quarks (or Strange and Charm), and the two leptons, the muon and muon-neutrino. The third, and apparently final, generation has the B- and T-quarks (or Bottom and Top) with the tau and the tau-neutrino. These are much more massive than the second generation, but otherwise identical. While abundant in the first moments of Creation, the second and third generations play no apparent role in the current universe, which prompted the famous "Who ordered that?" exclamation by theorist Isidor I. Rabi when the muon was first identified in cosmic ray showers.
Quarks are the only fundamental particles that interact through all four of the fundamental forces. Ignoring gravity, quarks can couple withâcreate and absorbâthe gluons of the strong force, the photons of the electromagnetic force, and the vector bosons of the weak force. In contrast, the electron can couple with photons and vector bosons, while the neutrino can only couple with vector bosons.
The color charge on the quarks comes in three paired varieties (unlike the single positive-negative pair of the electric charge) called red-antired, blue-antiblue, and green-antigreen. The colorless baryons with three quarks have one each of R, G, and B. Rather like the pixels of an RGB TV, all three together make white which accounts for the terminology. It must be emphasized, however, that the color charges on the quarks have nothing to do with the colors of everyday life.
Free quarks
No search for free quarks or fractional electric charges has returned convincing evidence. The absence of free quarks has therefore been incorporated into the notion of confinement, which, it is believed, the theory of quarks must possess.
Confinement began as an experimental observation, and is expected to follow from the modern theory of strong interactions, called quantum chromodynamics (QCD). Although there is no mathematical derivation of confinement in QCD, it is easy to show using lattice gauge theory.
However, it may be possible to change the confinement by creating dense or hot quark matter. These new phases of QCD matter have been predicted theoretically, and experimental searches for them have now started.
Confinement and quark properties
Every subatomic particle is completely described by a small set of observables such as mass m and quantum numbers, such as spin S and parity P. Usually these properties are directly determined by experiments. However, confinement makes it impossible to measure these properties of quarks. Instead, they must be inferred from measurable properties of the composite particles which are made up of quarks. Such inferences are usually most easily made for certain additive quantum numbers called flavors.
The composite particles made of quarks and antiquarks are the hadrons. These include the mesons which get their quantum numbers from a quark and an antiquark, and the baryons, which get theirs from three quarks. The quarks (and antiquarks) that impart quantum numbers to hadrons are called valence quarks. Apart from these, any hadron may contain an indefinite number of virtual quarks, antiquarks, and gluons which together contribute nothing to their quantum numbers. Such virtual quarks are called sea quarks.
Flavor
Each quark is assigned a baryon number, B = 1/3, and a vanishing lepton number, L = 0. They have fractional electric charge, Q, either Q = +2/3 or Q = â1/3. The former are called up-type quarks, the latter, down-type quarks. Each quark is assigned a weak isospin: Tz = +1/2 for an up-type quark and Tz = â1/2 for a down-type quark. Each doublet of weak isospin defines a generation of quarks. There are three generations, and hence six flavors of quarksâthe up-type quark flavors are up, charm, and top; the down-type quark flavors are down, strange, and bottom (each list is in the order of increasing mass).
The number of generations of quarks and leptons are equal in the standard model. The number of generations of leptons with a light neutrino is strongly constrained by experiments at the LEP in CERN and by observations of the abundance of helium in the universe. Precision measurement of the lifetime of the Z boson at LEP constrains the number of light neutrino generations to be three. Astronomical observations of helium abundance give consistent results. Results of direct searches for a fourth generation give limits on the mass of the lightest possible fourth-generation quark. The most stringent limit comes from analysis of results from the Tevatron collider at Fermilab, and shows that the mass of a fourth-generation quark must be greater than 190 GeV. Additional limits on extra quark generations come from measurements of quark mixing performed by the experiments Belle and BaBar.
Each flavor defines a quantum number which is conserved under the strong interactions, but not the weak interactions. The magnitude of flavor changing in the weak interaction is encoded into a structure called the CKM matrix. This also encodes the CP violation allowed in the Standard Model. The flavor quantum numbers are described in detail in the article on flavor.
Spin
Quantum numbers corresponding to non-Abelian symmetries like rotations require more care in extraction, since they are not additive. In the quark model one builds mesons out of a quark and an antiquark, whereas baryons are built from three quarks. Since mesons are bosons (having integer spins) and baryons are fermions (having half-integer spins), the quark model implies that quarks are fermions. Further, the fact that the lightest baryons have spin-1/2 implies that each quark can have spin S = 1/2. The spins of excited mesons and baryons are completely consistent with this assignment.
Color
Since quarks are fermions, the Pauli exclusion principle implies that the three valence quarks must be in an antisymmetric combination in a baryon. However, the charge Q = 2 baryon, Î++ (which is one of four isospin Iz = 3/2 baryons), can only be made of three u quarks with parallel spins. Since this configuration is symmetric under interchange of the quarks, it implies that there exists another internal quantum number, which would then make the combination antisymmetric. This is given the name "color," although it has nothing to do with the perception of the frequency (or wavelength) of light, which is the usual meaning of color. This quantum number is the charge involved in the gauge theory called quantum chromodynamics (QCD).
The only other colored particle is the gluon, which is the gauge boson of QCD. Like all other non-Abelian gauge theories (and unlike quantum electrodynamics), the gauge bosons interact with one another by the same force that affects the quarks.
Color is a gauged SU(3) symmetry. Quarks are placed in the fundamental representation, 3, and hence come in three colors (red, green, and blue). Gluons are placed in the adjoint representation, 8, and hence come in eight varieties. For more on this, see the article on color charge.
Quark masses
Although one speaks of quark mass in the same way as the mass of any other particle, the notion of mass for quarks is complicated by the fact that quarks cannot be found free in nature. As a result, the notion of a quark mass is a theoretical construct, which makes sense only when one specifies exactly the procedure used to define it.
Current quark mass
The approximate chiral symmetry of quantum chromodynamics, for example, allows one to define the ratio between various (up, down, and strange) quark masses through combinations of the masses of the pseudo-scalar meson octet in the quark model through chiral perturbation theory, giving
The fact that the up quark has mass is important, since there would be no strong CP problem if it were massless. The absolute values of the masses are currently determined from QCD sum rules (also called spectral function sum rules) and lattice QCD. Masses determined in this manner are called current quark masses. The connection between different definitions of the current quark masses needs the full machinery of renormalization for its specification.
Valence quark mass
Another, older, method of specifying the quark masses was to use the Gell-Mann-Nishijima mass formula in the quark model, which connect hadron masses to quark masses. The masses so determined are called constituent quark masses, and are significantly different from the current quark masses defined above. The constituent masses do not have any further dynamical meaning.
Heavy quark masses
The masses of the heavy charm and bottom quarks are obtained from the masses of hadrons containing a single heavy quark (and one light antiquark or two light quarks) and from the analysis of quarkonia. Lattice QCD computations using the heavy quark effective theory (HQET) or non-relativistic quantum chromodynamics (NRQCD) are currently used to determine these quark masses.
The top quark is sufficiently heavy that perturbative QCD can be used to determine its mass. Before its discovery in 1995, the best theoretical estimates of the top quark mass were obtained from global analysis of precision tests of the Standard Model. The top quark, however, is unique among quarks in that it decays before having a chance to hadronize. Thus, its mass can be directly measured from the resulting decay products. This can only be done at the Tevatron which is the only particle accelerator energetic enough to produce top quarks in abundance.
Properties of quarks
The following table summarizes the key properties of the six known quarks:
Generation Weak
IsospinFlavor Name Symbol Charge / e Mass / MeV·c-2 Antiparticle Symbol 1 +½ Iz=+½ Up u +â 1.5 â 4.0 Antiup 1 -½ Iz=-½ Down d -â 4 â 8 Antidown 2 -½ S=-1 Strange s -â 80 â 130 Antistrange 2 +½ C=1 Charm c +â 1150 â 1350 Anticharm 3 -½ B'=-1 Bottom b -â 4100 â 4400 Antibottom 3 +½ T=1 Top t +â 170900 ± 1800[1] Antitop
- Top quark mass from Tevatron Electroweak Working Group[2]
- Other quark masses from Particle Data Group[3]; these masses are given in the MS-bar scheme.
- The quantum numbers of the top and bottom quarks are sometimes known as truth and beauty respectively, as an alternative to topness and bottomness.
Antiquarks
The additive quantum numbers of antiquarks are equal in magnitude and opposite in sign to those of the quarks. CPT symmetry forces them to have the same spin and mass as the corresponding quark. Tests of CPT symmetry cannot be performed directly on quarks and antiquarks, due to confinement, but can be performed on hadrons. Notation of antiquarks follows that of antimatter in general: An up quark is denoted by , and an anti-up quark is denoted by .
Substructure
Some extensions of the Standard Model begin with the assumption that quarks and leptons have substructure. In other words, these models assume that the elementary particles of the Standard Model are in fact composite particles, made of some other elementary constituents. Such an assumption is open to experimental tests, and these theories are severely constrained by data. At present there is no evidence for such substructure. For more details see the article on preons.
History
The notion of quarks evolved out of a classification of hadrons developed independently in 1961 by Murray Gell-Mann and Kazuhiko Nishijima, which nowadays goes by the name of the quark model. The scheme grouped together particles with isospin and strangeness using a unitary symmetry derived from current algebra, which we today recognise as part of the approximate chiral symmetry of QCD. This is a global flavor SU(3) symmetry, which should not be confused with the gauge symmetry of QCD.
In this scheme the lightest mesons (spin-0) and baryons (spin-½) are grouped together into octets, 8, of flavor symmetry. A classification of the spin-3/2 baryons into the representation 10 yielded a prediction of a new particle, Ωâ, the discovery of which in 1964 led to wide acceptance of the model. The missing representation 3 was identified with quarks.
This scheme was called the eightfold way by Gell-Mann, a clever conflation of the octets of the model with the eightfold way of Buddhism. He also chose the name quark and attributed it to the sentence âThree quarks for Muster Markâ in James Joyce's Finnegans Wake.[4] The negative results of quark search experiments caused Gell-Mann to hold that quarks were mathematical fiction.
Analysis of certain properties of high energy reactions of hadrons led Richard Feynman to postulate substructures of hadrons, which he called partons (since they form part of hadrons). A scaling of deep inelastic scattering cross sections derived from current algebra by James Bjorken received an explanation in terms of partons. When Bjorken scaling was verified in an experiment in 1969, it was immediately realized that partons and quarks could be the same thing. With the proof of asymptotic freedom in QCD in 1973 by David Gross, Frank Wilczek, and David Politzer, the connection was firmly established.
The charm quark was postulated by Sheldon Glashow, Iliopoulos, and Maiani in 1970 to prevent unphysical flavor changes in weak decays which would otherwise occur in the standard model. The discovery in 1975 of the meson, which came to be called the J/Ï, led to the recognition that it was made of a charm quark and its antiquark.
The existence of a third generation of quarks was predicted in 1973 by Makoto Kobayashi and Toshihide Maskawa who realized that the observed violation of CP symmetry by neutral kaons could not be accommodated into the Standard Model with two generations of quarks. The bottom quark was discovered in 1977 and the top quark in 1996 at the Tevatron collider in Fermilab.
See also
Notes
- â Summary of Top Mass Results - March 2007. Retrieved September 14, 2007.
- â Tevatron Electroweak Working Group. Retrieved March 5, 2008.
- â Particle Data Group. Retrieved March 5, 2008.
- â Quark. American Heritage® Dictionary. Retrieved September 14, 2007.
ReferencesISBN links support NWE through referral fees
- Gell-Mann, Murray. 1964. A Schematic Model of Baryons and Mesons. Retrieved September 14, 2007.
- Gribbin, John. 1998. Richard Feynman: A Life in Science. New York, NY: Plume (Penguin). ISBN 0452276314
- Griffiths, David J. 1987. Introduction to Elementary Particles. New York, NY: Wiley. ISBN 0-471-60386-4
- Halzen, Francis, and Alan D. Martin. 1984. Quarks and Leptons: An Introductory Course in Modern Particle Physics. New York, NY: Wiley. ISBN 0471887412
- Povh, Bogdan. 1995. Particles and Nuclei: An Introduction to the Physical Concepts. Berlin, Germany: Springer-Verlag. ISBN 0-387-59439-6
- Observation of the top quark at Fermilab. Retrieved September 14, 2007.
- Particle Data Group on quarks. Retrieved September 14, 2007.
| Particles in physics | |
|---|---|
| elementary particles | Elementary fermions: Quarks: u · d · s · c · b · t ⢠Leptons: e · μ · Ï Â· νe · νμ · Î½Ï Elementary bosons: Gauge bosons: γ · g · W± · Z0 ⢠Ghosts |
| Composite particles | Hadrons: Baryons(list)/Hyperons/Nucleons: p · n · Π· Π· Σ · Π· Ω · Îb ⢠Mesons(list)/Quarkonia: Ï Â· K · Ï Â· J/Ï Â· Î¥ Other: Atomic nucleus ⢠Atoms ⢠Molecules ⢠Positronium |
| Hypothetical elementary particles | Superpartners: Axino · Dilatino · Chargino · Gluino · Gravitino · Higgsino · Neutralino · Sfermion · Slepton · Squark Other: Axion · Dilaton · Goldstone boson · Graviton · Higgs boson · Tachyon · X · Y · W' · Z' |
| Hypothetical composite particles | Exotic hadrons: Exotic baryons: Pentaquark ⢠Exotic mesons: Glueball · Tetraquark Other: Mesonic molecule |
| Quasiparticles | Davydov soliton · Exciton · Magnon · Phonon · Plasmon · Polariton · Polaron |
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.








