Coriolis effect

Figure 1: In the inertial frame of reference (upper part of the picture), the black object moves in a straight line. However, the observer (red dot) who is standing in the rotating frame of reference (lower part of the picture) sees the object as following a curved path.

In physics, the Coriolis effect is an apparent deflection of moving objects when they are viewed from a rotating frame of reference. It is named after Gaspard-Gustave Coriolis, a French scientist who described it in 1835, though the mathematics appeared in the tidal equations of Pierre-Simon Laplace in 1778.

This effect is caused by the Coriolis force, which appears in the equation of motion of an object in a rotating frame of reference. It is an example of a fictitious force (or pseudo force), because it does not appear when the motion is expressed in an inertial frame of reference, in which the motion of an object is explained by the real impressed forces, together with inertia. In a rotating frame, the Coriolis force, which depends on the velocity of the moving object, and centrifugal force, which does not depend on the velocity of the moving object, are needed in the equation to correctly describe the motion.

Perhaps the most commonly encountered rotating reference frame is the Earth. Freely moving objects on the surface of the Earth experience a Coriolis force, and appear to veer to the right in the northern hemisphere, and to the left in the southern. Movements of air in the atmosphere and water in the ocean are notable examples of this behavior: rather than flowing directly from areas of high pressure to low pressure, as they would on a non-rotating planet, winds and currents tend to flow to the right of this direction north of the equator, and to the left of this direction south of the equator. This effect is responsible for the rotation of large cyclones and tornados.

Formula

In non-vector terms: at a given rate of rotation of the observer, the magnitude of the Coriolis acceleration of the object is proportional to the velocity of the object and also to the sine of the angle between the direction of movement of the object and the axis of rotation.

The vector formula for the magnitude and direction the Coriolis acceleration is

${\boldsymbol {a}}_{C}=-2\,{\boldsymbol {\Omega \times v}}$

where (here and below) v is the velocity of the particle in the rotating system, and Ω is the angular velocity vector which has magnitude equal to the rotation rate ω and is directed along the axis of rotation of the rotating reference frame, and the × symbol represents the cross product operator.

The equation may be multiplied by the mass of the relevant object to produce the Coriolis force:

${\boldsymbol {F}}_{C}=-2\,m\,{\boldsymbol {\Omega \times v}}$.

See fictitious force for a derivation.

The Coriolis effect is the behavior added by the Coriolis acceleration. The formula implies that the Coriolis acceleration is perpendicular both to the direction of the velocity of the moving mass and to the frame's rotation axis. So in particular:

• if the velocity is parallel to the rotation axis, the Coriolis acceleration is zero
• if the velocity is straight inward to the axis, the acceleration is in the direction of local rotation
• if the velocity is straight outward from the axis, the acceleration is against the direction of local rotation
• if the velocity is in the direction of local rotation, the acceleration is outward from the axis
• if the velocity is against the direction of local rotation, the acceleration is inward to the axis

The vector cross product can be evaluated as the determinant of a matrix:

${\boldsymbol {\Omega \times v}}={\begin{vmatrix}{\boldsymbol {i}}&{\boldsymbol {j}}&{\boldsymbol {k}}\\\Omega _{x}&\Omega _{y}&\Omega _{z}\\v_{x}&v_{y}&v_{z}\end{vmatrix}}\ ={\begin{pmatrix}\Omega _{y}v_{z}-\Omega _{z}v_{y}\\\Omega _{z}v_{x}-\Omega _{x}v_{z}\\\Omega _{x}v_{y}-\Omega _{y}v_{x}\end{pmatrix}}\ ,$

where the vectors i, j, k are unit vectors in the x, y and z directions.

Rotating sphere

Figure 2: Coordinate system at latitude φ with x-axis east, y-axis north and z-axis upward (that is, radially outward from center of sphere).

Consider a location with latitude $\varphi$ on a sphere that is rotating around the north-south axis. A local coordinate system is set up with the $x$ axis horizontally due east, the $y$ axis horizontally due north and the $z$ axis vertically upwards. The rotation vector, velocity of movement and Coriolis acceleration expressed in this local coordinate system (listing components in the order East (e), North (n) and Upward (u)) are:

${\boldsymbol {\Omega }}=\omega {\begin{pmatrix}0\\\cos \varphi \\\sin \varphi \end{pmatrix}}\ ,$     ${\boldsymbol {v}}={\begin{pmatrix}v_{e}\\v_{n}\\v_{u}\end{pmatrix}}\ ,$

${\boldsymbol {a}}_{C}=-2{\boldsymbol {\Omega \times v}}=2\,\omega \,{\begin{pmatrix}v_{n}\sin \varphi -v_{u}\cos \varphi \\-v_{e}\sin \varphi \\v_{e}\cos \varphi \end{pmatrix}}\ .$

When considering atmospheric or oceanic dynamics, the vertical velocity is small and the vertical component of the Coriolis acceleration is small compared to gravity. For such cases, only the horizontal (East and North) components matter. The restriction of the above to the horizontal plane is (setting v_u=0):

${\boldsymbol {v}}={\begin{pmatrix}v_{e}\\v_{n}\end{pmatrix}}\ ,$     ${\boldsymbol {a}}_{c}={\begin{pmatrix}v_{n}\\-v_{e}\end{pmatrix}}\ f\ ,$

where $f=2\omega \sin \varphi \,$ is called the Coriolis parameter.

By setting v_n = 0, it can be seen immediately that (for positive $\varphi$ and $\omega \,$) a movement due east results in an acceleration due south. Similarly, setting v_e = 0, it is seen that a movement due north results in an acceleration due east — that is, standing on the horizontal plane, looking along the direction of the movement causing the acceleration, the acceleration always is turned 90° to the right. That is:

On a merry-go-round in the night
Coriolis was shaken with fright
Despite how he walked
'Twas like he was stalked
By some fiend always pushing him right

David Morin, Eric Zaslow, E'beth Haley, John Golden, and Nathan Salwen

As a different case, consider equatorial motion setting φ = 0°. In this case, Ω is parallel to the North or n-axis, and:

${\boldsymbol {\Omega }}=\omega {\begin{pmatrix}0\\1\\0\end{pmatrix}}\ ,$     ${\boldsymbol {v}}={\begin{pmatrix}v_{e}\\v_{n}\\v_{u}\end{pmatrix}}\ ,$  ${\boldsymbol {a}}_{C}=-2{\boldsymbol {\Omega \times v}}=2\,\omega \,{\begin{pmatrix}-v_{u}\\0\\v_{e}\end{pmatrix}}\ .$

Accordingly, an eastward motion (that is, in the same direction as the rotation of the sphere) provides an upward acceleration known as the Eötvös effect, and an upward motion produces an acceleration due west.

For additional examples, see rotating spheres and dropping ball in the article on centrifugal force, and carousel in fictitious force.

Causes

The Coriolis effect exists only when using a rotating reference frame. It is mathematically deduced from the law of inertia. Hence it does not correspond to any actual acceleration or force, but only the appearance thereof from the point of view of a rotating system.

That said, a denizen of a rotating frame, such as an astronaut in a rotating space station, very probably will find the interpretation of everyday life in terms of the Coriolis force accords more simply with intuition and experience than a cerebral reinterpretation of events from an inertial standpoint. For example, nausea due to an experienced push may be more instinctively explained by Coriolis force than by the law of inertia. See also Coriolis effect (perception).

The Coriolis effect exhibited by a moving object can be interpreted as being the sum of the effects of two different causes of equal magnitude. For a mathematical formulation see fictitious force.

The first cause is the change of the velocity of an object in time. The same velocity (in an inertial frame of reference where the normal laws of physics apply) will be seen as different velocities at different times in a rotating frame of reference. The apparent acceleration is proportional to the angular velocity of the reference frame (the rate at which the coordinate axes changes direction), and to the velocity of the object. This gives a term $-{\boldsymbol {\Omega }}\times \mathbf {v}$. The minus sign arises from the traditional definition of the cross product (right hand rule), and from the sign convention for angular velocity vectors.

The second cause is change of velocity in space. Different points in a rotating frame of reference have different velocities (as seen from an inertial frame of reference). In order for an object to move in a straight line it must therefore be accelerated so that its velocity changes from point to point by the same amount as the velocities of the frame of reference. The effect is proportional to the angular velocity (which determines the relative speed of two different points in the rotating frame of reference), and the velocity of the object perpendicular to the axis of rotation (which determines how quickly it moves between those points). This also gives a term $-{\boldsymbol {\Omega }}\times \mathbf {v}$.

Corrections to common misconceptions about the Coriolis effect

• The Coriolis effect does not have a significant impact on the swirl of the flushing water of a toilet. Indeed, the direction of the swirl is mainly defined by the direction with which the water is introduced in the toilet, which has a much higher impact than the Coriolis effect
• In theory, in a perfect sink, the Coriolis effect would define the direction of the swirl, as has been proved by Ascher Shapiro in 1962. Nevertheless, any imperfection of the sink, or initial rotation of the water, can compensate for the Coriolis effect, due to its very low amplitude.
• The Coriolis effect is not a result of the curvature of the Earth, only of its rotation. (However, the value of the Coriolis parameter, $f\$, does vary with latitude, and that dependence is due to the Earth's shape.)
• Ballistic missiles and satellites appear to follow curved paths when plotted on common world maps mainly because the earth is spherical and the shortest distance between two points on the earth's surface (called a great circle) is usually not a straight line on those maps. Every two-dimensional (flat) map necessarily distorts the earth's curved (three-dimensional) surface in some way. Typically (as in the commonly used Mercator projection, for example), this distortion increases with proximity to the poles. In the northern hemisphere for example, a ballistic missile fired toward a distant target using the shortest possible route (a great circle) will appear on such maps to follow a path north of the straight line from target to destination, and then curve back toward the equator. This occurs because the latitudes, which are projected as straight horizontal lines on most world maps, are in fact circles on the surface of a sphere, which get smaller as they get closer to the pole. Being simply a consequence of the sphericity of the Earth, this would be true even if the Earth didn't rotate. The Coriolis effect is of course also present, but its effect on the plotted path is much smaller.
• The Coriolis force should not be confused with the centrifugal force given by $m{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times \mathbf {r} )$. A rotating frame of reference will always cause a centrifugal force no matter what the object is doing (unless that body is particle-like and lies on the axis of rotation), whereas the Coriolis force requires the object to be in motion relative to the rotating frame with a velocity that is not parallel to the rotation axis. Because the centrifugal force always exists, it can be easy to confuse the two, making simple explanations of the effect of Coriolis in isolation difficult. In particular, when $\mathbf {v}$ is tangential to a circle centered on and perpendicular to the axis of rotation, the Coriolis force is parallel to the centrifugal force. In a rotating reference frame with a rotational speed equal to that of the object, the apparent velocity of the object $\mathbf {v}$ is zero, and there is no Coriolis force.

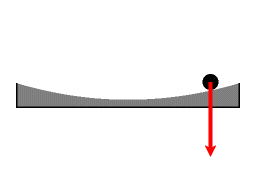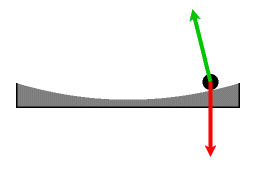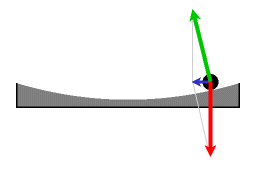
Cannon on turntable

Figure 3: Cannon on a rotating turntable. To hit the target located at position 1 at time t = 0s, the cannon must be aimed ahead of the target at angle θ. That way, by the time the cannonball reaches position 3 on the periphery, the target also will be at that position. In an inertial frame of reference, the cannonball travels a straight radial path to the target (curve y_A). However, in the frame of the turntable, the path is arched (curve y_B), as also shown in the figure.

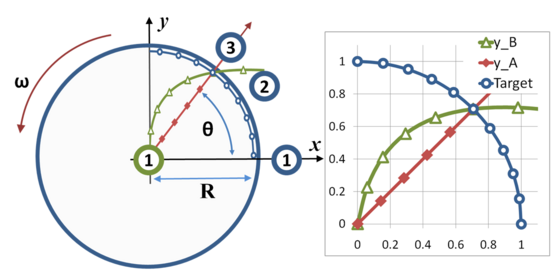
Figure 1 is an animation of the classic illustration of Coriolis force. Another visualization of the Coriolis and centrifugal forces is this animation clip. Figure 3 is a graphical version.

Here is a question: given the radius of the turntable R, the rate of angular rotation ω, and the speed of the cannonball (assumed constant) v, what is the correct angle θ to aim so as to hit the target at the edge of the turntable?

The inertial frame of reference provides one way to handle the question: calculate the time to interception, which is t_f = R / v. Then, the turntable revolves an angle ω t_f in this time. If the cannon is pointed an angle θ = ω t_f = ω R / v, then the cannonball arrives at the periphery at position number 3 at the same time as the target.

No discussion of Coriolis force can arrive at this solution as simply, so the reason to treat this problem is to demonstrate Coriolis formalism in an easily visualized situation.

Formulation

Figure 4: Successful trajectory of cannonball as seen from the turntable for three angles of launch θ. Plotted points are for the same equally spaced times steps on each curve. Cannonball speed v is held constant and angular rate of rotation ω is varied to achieve a successful "hit" for selected θ. For example, for a radius of 1 m and a cannonball speed of 1 m/s, the time of flight t_f = 1 s, and ωt_f = θ → ω and θ have the same numerical value if θ is expressed in radians. The wider spacing of the plotted points as the target is approached show the speed of the cannonball is accelerating as seen on the turntable, due to fictitious Coriolis and centrifugal forces.

Figure 5: Acceleration components at an earlier time (top) and at arrival time at the target (bottom)

Figure 6: Coriolis acceleration, centrifugal acceleration and net acceleration vectors at three selected points on the trajectory as seen on the turntable.

The trajectory in the inertial frame (denoted A) is a straight line radial path at angle θ. The position of the cannonball in ( x, y ) coordinates at time t is:

$\mathbf {r} _{A}(t)$ $=vt\ \left(\cos(\theta ),\right.$$\left.{\color {white}..}\ \sin(\theta )\right)\ .$

In the turntable frame (denoted B), the x- y axes rotate at angular rate ω, so the trajectory becomes:

$\mathbf {r} _{B}(t)$   $=vt\ \left(\cos(\theta -\omega t),\right.$$\left.{\color {white}..}\sin(\theta -\omega t)\right)\ ,$

and three examples of this result are plotted in Figure 4.

To determine the components of acceleration, a general expression is used from the article fictitious force:

$\mathbf {a} _{B}=\mathbf {a} _{A}$ $-2{\boldsymbol {\Omega }}\times \mathbf {v} _{B}$ $-{\boldsymbol {\Omega }}\times ({\boldsymbol {\Omega }}\times \mathbf {r} _{B})$ $-{\frac {d{\boldsymbol {\Omega }}}{dt}}\times \mathbf {r} _{B}\ ,$

in which the term in Ω × v_B is the Coriolis acceleration and the term in Ω × ( Ω × r_B) is the centrifugal acceleration. The results are (let α = θ − ωt):

${\boldsymbol {\Omega }}\mathbf {\times r_{B}}$ $={\begin{vmatrix}{\boldsymbol {i}}&{\boldsymbol {j}}&{\boldsymbol {k}}\\0&0&\omega \\vt\cos \alpha &vt\sin \alpha &0\end{vmatrix}}\$ $=\omega tv\left(-\sin \alpha ,\cos \alpha \right)\ ,$

${\boldsymbol {\Omega \ \times }}\left({\boldsymbol {\Omega }}\mathbf {\times r_{B}} \right)$ $={\begin{vmatrix}{\boldsymbol {i}}&{\boldsymbol {j}}&{\boldsymbol {k}}\\0&0&\omega \\-\omega tv\sin \alpha &\omega tv\cos \alpha &0\end{vmatrix}}\ \ ,$

producing a centrifugal acceleration:

$\mathbf {a_{\mathrm {Cfgl} }}$ $=\omega ^{2}vt\left(\cos \alpha ,\sin \alpha \right)=\omega ^{2}\mathbf {r_{B}} (t)\ .$

Also:

${\boldsymbol {\Omega }}\mathbf {\times v_{B}}$  $={\begin{vmatrix}\!{\boldsymbol {i}}&\!{\boldsymbol {j}}&\!{\boldsymbol {k}}\\0&0&\omega \\v\cos \alpha \quad &v\sin \alpha \quad &\quad \\\;+\omega t\ v\sin \alpha &\;-\omega t\ v\cos \alpha &0\end{vmatrix}}\ \ ,$

producing a Coriolis acceleration:

$\mathbf {a_{\mathrm {Cor} }}$ $=-2\left[-\omega v\left(\sin \alpha -\omega t\cos \alpha \right),\right.$$\left.{\color {white}...}\ \omega v\left(\cos \alpha +\omega t\sin \alpha \right)\right]\$

$=2\omega v\left(\sin \alpha ,\ -\cos \alpha \right)$ $-2\omega ^{2}\mathbf {r_{B}} (t)\ .$

Figure 5 and Figure 6 show these accelerations for a particular example.

It is seen that the Coriolis acceleration not only cancels the centrifugal acceleration, but together they provide a net "centripetal," radially inward component of acceleration (that is, directed toward the center of rotation) :

$\mathbf {a_{\mathrm {Cptl} }} =-\omega ^{2}\mathbf {r_{B}} (t)\ ,$

and an additional component of acceleration perpendicular to r_B (t):

$\mathbf {a_{C\perp }}$ $=2\omega v\left(\sin \alpha ,\ -\cos \alpha \right)\ .$

The "centripetal" component of acceleration resembles that for circular motion at radius r_B, while the perpendicular component is velocity dependent, increasing with the radial velocity v and directed to the right of the velocity. The situation could be described as a circular motion combined with an "apparent Coriolis acceleration" of 2ωv. However, this is a rough labeling: a careful designation of the true centripetal force refers to a local reference frame that employs the directions normal and tangential to the path, not coordinates referred to the axis of rotation.

These results also can be obtained directly by two time differentiations of r_B (t). Agreement of the two approaches demonstrates that one could start from the general expression for fictitious acceleration above and derive the trajectories of Figure 4. However, working from the acceleration to the trajectory is more complicated than the reverse procedure used here, which, of course, is made possible in this example by knowing the answer in advance.

As a result of this analysis an important point appears: all the fictitious accelerations must be included to obtain the correct trajectory. In particular, besides the Coriolis acceleration, the centrifugal force plays an essential role. It is easy to get the impression from verbal discussions of the cannonball problem, which are focused on displaying the Coriolis effect particularly, that the Coriolis force is the only factor that must be considered; emphatically, that is not so. A turntable for which the Coriolis force is the only factor is the parabolic turntable. A somewhat more complex situation is the idealized example of flight routes over long distances, where the centrifugal force of the path and aeronautical lift are countered by gravitational attraction.

Tossed ball on a rotating carousel

Figure 7: A carousel is rotating counterclockwise. Left panel:a ball is tossed by a thrower at 12:00 o'clock and it travels in a straight line to the center of the carousel. While it travels, the thrower circles in a counterclockwise direction. Right panel: The ball's motion as seen by the thrower, who now remains at 12:00 o'clock, because there is no rotation from their viewpoint.

Figure 7 illustrates a ball tossed from 12:00 o'clock toward the center of a counterclockwise rotating carousel. On the left, the ball is seen by a stationary observer above the carousel, and the ball travels in a straight line to the center, while the ball-thrower rotates counterclockwise with the carousel. On the right the ball is seen by an observer rotating with the carousel, so the ball-thrower appears to stay at 12:00 o'clock. The figure shows how the trajectory of the ball as seen by the rotating observer can be constructed.

On the left, two arrows locate the ball relative to the ball-thrower. One of these arrows is from the thrower to the center of the carousel (providing the ball-thrower's line of sight), and the other points from the center of the carousel to the ball. (This arrow gets shorter as the ball approaches the center.) A shifted version of the two arrows is shown dotted.

On the right is shown this same dotted pair of arrows, but now the pair are rigidly rotated so the arrow corresponding to the line of sight of the ball-thrower toward the center of the carousel is aligned with 12:00 o'clock. The other arrow of the pair locates the ball relative to the center of the carousel, providing the position of the ball as seen by the rotating observer. By following this procedure for several positions, the trajectory in the rotating frame of reference is established as shown by the curved path in the right-hand panel.

The ball travels in the air, and there is no net force upon it. To the stationary observer the ball follows a straight-line path, so there is no problem squaring this trajectory with zero net force. However, the rotating observer sees a curved path. Kinematics insists that a force (pushing to the right of the instantaneous direction of travel for a counterclockwise rotation) must be present to cause this curvature, so the rotating observer is forced to invoke a combination of centrifugal and Coriolis forces to provide the net force required to cause the curved trajectory.

Bounced ball

Figure 8: Bird's-eye view of carousel. The carousel rotates clockwise. Two viewpoints are illustrated: that of the camera at the center of rotation rotating with the carousel (left panel) and that of the inertial (stationary) observer (right panel). Both observers agree at any given time just how far the ball is from the center of the carousel, but not on its orientation. Time intervals are 1/10 of time from launch to bounce.

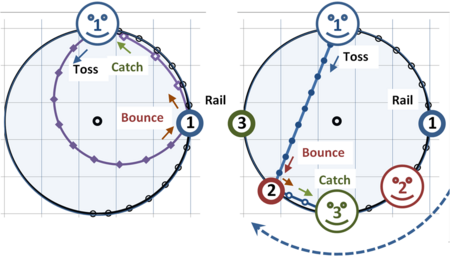
Figure 8 describes a more complex situation where the tossed ball on a turntable bounces off the edge of the carousel and then returns to the tosser, who catches the ball. The effect of Coriolis force on its trajectory is shown again as seen by two observers: an observer (referred to as the "camera") that rotates with the carousel, and an inertial observer. Figure 8 shows a bird's-eye view based upon the same ball speed on forward and return paths. Within each circle, plotted dots show the same time points. In the left panel, from the camera's viewpoint at the center of rotation, the tosser (smiley face) and the rail both are at fixed locations, and the ball makes a very considerable arc on its travel toward the rail, and takes a more direct route on the way back. From the ball tosser's viewpoint, the ball seems to return more quickly than it went (because the tosser is rotating toward the ball on the return flight).

On the carousel, instead of tossing the ball straight at a rail to bounce back, the ball must be thrown toward the center of the carousel and then seems to the camera to bear left from the direction of travel to hit the rail (left because the carousel is turning clockwise). The ball appears to bear to the left from direction of travel on both inward and return trajectories. The curved path demands this observer to recognize a leftward net force on the ball. (This force is "fictitious" because it disappears for a stationary observer.) For some angles of launch, a path has portions where the trajectory is approximately radial, and Coriolis force is primarily responsible for the apparent deflection of the ball (centrifugal force is radial from the center of rotation, and causes little deflection on these segments). When a path curves away from radial, however, centrifugal force contributes significantly to deflection.

The ball's path through the air is straight when viewed by observers standing on the ground (right panel). In the right panel (stationary observer), the ball tosser (smiley face) is at 12 o'clock and the rail the ball bounces from is at position one (1). From the inertial viewer's standpoint, positions one (1), two (2), three (3) are occupied in sequence. At position 2 the ball strikes the rail, and at position 3 the ball returns to the tosser. Straight-line paths are followed because the ball is in free flight, so this observer requires that no net force is applied.

A video clip of the tossed ball and other experiments are found at youtube: coriolis effect (2-11), University of Illinois WW2010 Project (some clips repeat only a fraction of a full rotation), and youtube.

Some mathematical details

What follows are some details of calculation of the trajectories. The path from the camera's viewpoint is related to that of the stationary observer by taking into account the rotation at an angular rate ω. If we let the path in inertial coordinates be (x, y) and in rotating coordinates (x', y'), then the path from the camera's viewpoint is (see matrix multiplication):

${\begin{pmatrix}x'(t)\\y'(t)\end{pmatrix}}={\begin{pmatrix}\cos(\omega t)&-\sin(\omega t)\\\sin(\omega t)&\cos(\omega t)\end{pmatrix}}{\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}\ ,$

assuming that at t = 0 s the two coordinate systems are aligned. A quarter rotation later, cos(ωt) = cos(π/2) = 0, and sin(ωt) = sin(π/2) = 1, and the transformation shows the x' -axis lies along the negative y-axis, while the y' -axis lies along the positive x-axis, as expected for clockwise rotation.

Visualization of the Coriolis effect

Figure 9: A fluid assuming a parabolic shape as it is rotating

Figure 10: The forces at play in the case of a curved surface.
Red : gravity
Green : the normal force
Blue : the resultant centripetal force.

Figure 11: Object moving frictionlessly over the surface of a very shallow parabolic dish. The object has been released in such a way that it follows an ellipse-shaped trajectory.
Left: The inertial point of view.
Right: The co-rotating point of view.

To demonstrate the Coriolis effect, a parabolic turntable can be used. On a flat turntable, the inertia of a co-rotating object would force it off the edge. But if the surface of the turntable has the correct parabolic bowl shape and is rotated at the correct rate, the force components shown in Figure 10 are arranged so the component of gravity tangential to the bowl surface will exactly equal the centripetal force necessary to keep the object rotating at its velocity and radius of curvature (assuming no friction). (See banked turn.) This carefully contoured surface allows the Coriolis force to be displayed in isolation.

Discs cut from cylinders of dry ice can be used as pucks, moving around almost frictionlessly over the surface of the parabolic turntable, allowing effects of Coriolis on dynamic phenomena to show themselves. To get a view of the motions as seen from the reference frame rotating with the turntable, a video camera is attached to the turntable so as to co-rotate with the turntable, with results as shown in Figure 11. In the left panel of Figure 11, which is the viewpoint of a stationary observer, the gravitational force in the inertial frame pulling the object toward the center (bottom ) of the dish is proportional to the distance of the object from the center. A centripetal force of this form causes the elliptical motion. In the right panel, which shows the viewpoint of the rotating frame, the inward gravitational force in the rotating frame (the same force as in the inertial frame) is balanced by the outward centrifugal force (present only in the rotating frame). With these two forces balanced, in the rotating frame the only unbalanced force is Coriolis (also present only in the rotating frame), and the motion is an inertial circle. Analysis and observation of circular motion in the rotating frame is a simplification compared to analysis or observation of elliptical motion in the inertial frame.

Because this reference frame rotates several times a minute, rather than only once a day like the Earth, the Coriolis acceleration produced is many times larger, and so easier to observe on small time and spatial scales, than is the Coriolis acceleration caused by the rotation of the Earth.

In a manner of speaking, the Earth is analogous such a turntable. The rotation has caused the planet to settle on a spheroid shape such that the normal force, the gravitational force, and the centrifugal force exactly balance each other on a "horizontal" surface. (See equatorial bulge.)

The Coriolis effect caused by the rotation of the Earth can be seen indirectly through the motion of a Foucault pendulum.

Length scales and the Rossby number

The time, space and velocity scales are important in determining the importance of the Coriolis effect. Whether rotation is important in a system can be determined by its Rossby number, which is the ratio of the velocity, $U$, of a system to the product of the Coriolis parameter, $f$, and the length scale, $L$, of the motion:

$Ro={\frac {U}{fL}}$.

The Rossby number is the ratio of centrifugal to Coriolis accelerations. A small Rossby number signifies a system which is strongly affected by Coriolis forces, and a large Rossby number signifies a system in which centrifugal forces dominate. For example, in tornadoes, the Rossby number is large, in low-pressure systems it is low and in oceanic systems it is of the order of unity. As a result, in tornadoes the Coriolis force is negligible, and balance is between pressure and centrifugal forces. In low-pressure systems, centrifugal force is negligible and balance is between Coriolis and pressure forces. In the oceans all three forces are comparable.

An atmospheric system moving at U = 10 m/s occupying a spatial distance of L = 1000 km, has a Rossby number of approximately 0.1. A man playing catch may throw the ball at U = 30 m/s in a garden of length L = 50 m. The Rossby number in this case would be about = 6000. Needless to say, one does not worry about which hemisphere one is in when playing catch in the garden. However, an unguided missile obeys exactly the same physics as a baseball, but may travel far enough and be in the air long enough to notice the effect of Coriolis. Long-range shells in the Northern Hemisphere landed close to, but to the right of, where they were aimed until this was noted. (Those fired in the southern hemisphere landed to the left.) In fact, it was this effect that first got the attention of Coriolis himself.

Draining in bathtubs and toilets

A misconception in popular culture is that water in bathtubs or toilets always drains in one direction in the Northern Hemisphere, and in the other direction in the Southern Hemisphere as a consequence of the Coriolis effect. This idea has been perpetuated by several television programs, including an episode of The Simpsons and one of The X-Files. In addition, several science broadcasts and publications (including at least one college-level physics textbook) have made this incorrect statement.

The Rossby number can also tell us about the bathtub. If the length scale of the tub is about L = 1 m, and the water moves towards the drain at about U = 60 cm/s, then the Rossby number is about 6 000. Thus, the bathtub is, in terms of scales, much like a game of catch, and rotation is unlikely to be important. However, if the experiment is very carefully controlled to remove all other forces from the system, rotation can play a role in bathtub dynamics. An article in the British Journal of Fluid Mechanics in the 1930s describes this. The key is to put a few drops of ink into the bathtub water, and observing when the ink stops swirling, meaning the viscosity of the water has dissipated its initial vorticity (or curl; i.e. $\nabla \times U=0$) then, if the plug is extracted ever so slowly so as not to introduce any additional vorticity, then the tub will empty with a counterclockwise swirl in England.

Some sources that incorrectly attribute draining direction to the Coriolis force also get the direction wrong. If the Coriolis force were the dominant factor, drain vortices would spin counterclockwise in the northern hemisphere and clockwise in the southern.

In reality the Coriolis effect is a few orders of magnitude smaller than various random influences on drain direction, such as the geometry of the container and the direction in which water was initially added to it. Most toilets flush in only one direction, because the toilet water flows into the bowl at an angle. If water shot into the basin from the opposite direction, the water would spin in the opposite direction.

When the water is being drawn towards the drain, the radius of its rotation around the drain decreases, so its rate of rotation increases from the low background level to a noticeable spin in order to conserve its angular momentum (the same effect as ice skaters bringing their arms in to cause them to spin faster). As shown by Ascher Shapiro in a 1961 educational video (Vorticity, Part 1), this effect can indeed reveal the influence of the Coriolis force on drain direction, but only under carefully controlled laboratory conditions. In a large, circular, symmetrical container (ideally over 1m in diameter and conical), still water (whose motion is so little that over the course of a day, displacements are small compared to the size of the container) escaping through a very small hole, will drain in a cyclonic fashion: counterclockwise in the Northern hemisphere and clockwise in the Southern hemisphere—the same direction as the Earth rotates with respect to the corresponding poles.

Coriolis effects in meteorology

Figure 12: This low pressure system over Iceland spins counter-clockwise due to balance between the Coriolis force and the pressure gradient force.

Figure 13: Schematic representation of flow around a low-pressure area in the Northern hemisphere. The Rossby number is low, so the centrifugal force is negligible. The pressure-gradient force is represented by blue arrows, the Coriolis acceleration (always perpendicular to the velocity) by red arrows

Perhaps the most important instance of the Coriolis effect is in the large-scale dynamics of the oceans and the atmosphere. In meteorology and ocean science, it is convenient to use a rotating frame of reference where the Earth is stationary. The fictitious centrifugal and Coriolis forces must then be introduced. Their relative importance is determined by the Rossby number. Tornadoes have a high Rossby number, so Coriolis forces are unimportant, and are not discussed here. As discussed next, low-pressure areas are phenomena where Coriolis forces are significant.

Flow around a low-pressure area

If a low-pressure area forms in the atmosphere, air will tend to flow in towards it, but will be deflected perpendicular to its velocity by the Coriolis acceleration. A system of equilibrium can then establish itself creating circular movement, or a cyclonic flow. Because the Rossby number is low, the force balance is largely between the pressure gradient force acting towards the low-pressure area and the Coriolis force acting away from the center of the low pressure.

Instead of flowing down the gradient, large scale motions in the atmosphere and ocean tend to occur perpendicular to the pressure gradient. This is known as geostrophic flow. On a non-rotating planet fluid would flow along the straightest possible line, quickly eliminating pressure gradients. Note that the geostrophic balance is thus very different from the case of "inertial motions" (see below) which explains why mid-latitude cyclones are larger by an order of magnitude than inertial circle flow would be.

This pattern of deflection, and the direction of movement, is called Buys-Ballot's law. In the atmosphere, the pattern of flow is called a cyclone. In the Northern Hemisphere the direction of movement around a low-pressure area is counterclockwise. In the Southern Hemisphere, the direction of movement is clockwise because the rotational dynamics is a mirror image there. At high altitudes, outward-spreading air rotates in the opposite direction. Cyclones rarely form along the equator due to the weak Coriolis effect present in this region.

Inertial circles

Figure 14: Schematic representation of inertial circles of air masses in the absence of other forces, calculated for a wind speed of approximately 50 to 70 m/s. Note that the rotation is exactly opposite that normally experienced with air masses in weather systems around depressions.

An air or water mass moving with speed $v\,$ subject only to the Coriolis force travels in a circular trajectory called an 'inertial circle'. Since the force is directed at right angles to the motion of the particle, it will move with a constant speed, and perform a complete circle with frequency $f$. The magnitude of the Coriolis force also determines the radius of this circle:

$R=v/f\,$.

On the Earth, a typical mid-latitude value for $f$ is 10⁻⁴ s⁻¹; hence for a typical atmospheric speed of 10 m/s the radius is 100 km, with a period of about 14 hours. In the ocean, where a typical speed is closer to 10 cm/s, the radius of an inertial circle is 1 km. These inertial circles are clockwise in the northern hemisphere (where trajectories are bent to the right) and anti-clockwise in the southern hemisphere.

If the rotating system is a parabolic turntable, then $f$ is constant and the trajectories are exact circles. On a rotating planet, $f$ varies with latitude and the paths of particles do not form exact circles. Since the parameter $f$ varies as the sine of the latitude, the radius of the oscillations associated with a given speed are smallest at the poles (latitude = ±90°), and increase toward the equator.

Other terrestrial effects

The Coriolis effect strongly affects the large-scale oceanic and atmospheric circulation, leading to the formation of robust features like jet streams and western boundary currents. Such features are in geostrophic balance, meaning that the Coriolis and pressure gradient forces balance each other. Coriolis acceleration is also responsible for the propagation of many types of waves in the ocean and atmosphere, including Rossby waves and Kelvin waves. It is also instrumental in the so-called Ekman dynamics in the ocean, and in the establishment of the large-scale ocean flow pattern called the Sverdrup balance.

Other aspects of the Coriolis effect

The practical impact of the Coriolis effect is mostly caused by the horizontal acceleration component produced by horizontal motion.

There are other components of the Coriolis effect. Eastward-traveling objects will be deflected upwards (feel lighter), while westward-traveling objects will be deflected downwards (feel heavier). This is known as the Eötvös effect. This aspect of the Coriolis effect is greatest near the equator. The force produced by this effect is similar to the horizontal component, but the much larger vertical forces due to gravity and pressure mean that it is generally unimportant dynamically.

In addition, objects traveling upwards or downwards will be deflected to the west or east respectively. This effect is also the greatest near the equator. Since vertical movement is usually of limited extent and duration, the size of the effect is smaller and requires precise instruments to detect.

Coriolis effects in other areas

Coriolis flow meter

A practical application of the Coriolis effect is the mass flow meter, an instrument that measures the mass flow rate and density of a fluid flowing through a tube. The operating principle, introduced in 1977 by Micro Motion Inc., involves inducing a vibration of the tube through which the fluid passes. The vibration, though it is not completely circular, provides the rotating reference frame which gives rise to the Coriolis effect. While specific methods vary according to the design of the flow meter, sensors monitor and analyze changes in frequency, phase shift, and amplitude of the vibrating flow tubes. The changes observed represent the mass flow rate and density of the fluid.

Molecular physics

In polyatomic molecules, the molecule motion can be described by a rigid body rotation and internal vibration of atoms about their equilibrium position. As a result of the vibrations of the atoms, the atoms are in motion relative to the rotating coordinate system of the molecule. Coriolis effects will therefore be present and will cause the atoms to move in a direction perpendicular to the original oscillations. This leads to a mixing in molecular spectra between the rotational and vibrational levels.

Ballistics

The Coriolis effects became important in external ballistics for calculating the trajectories of very long-range artillery shells. The most famous historical example was the Paris gun, used by the Germans during World War I to bombard Paris from a range of about 120 km (75 mi).

Insect flight

Flies (Diptera) and moths (Lepidoptera) utilize the Coriolis effect when flying: their halteres, or antennae in the case of moths, oscillate rapidly and are used as vibrational gyroscopes. See Coriolis effect in insect stability. In this context, the Coriolis effect has nothing to do with the rotation of the Earth.

See also

• Classical mechanics
• Gyroscope
• Statics

References

ISBN links support NWE through referral fees

Physics and meteorology

• Barry, Roger Graham, and Richard J. Chorley. Atmosphere, Weather and Climate. London, UK: Rutledge, 2003. ISBN 0415271711.
• Butz, Stephen D. Science of Earth Systems. Clifton Park, NY: Thomson Delmar Learning, 2002. ISBN 0766833917.
• Carlucci, Donald E., and Sidney S. Jacobson. Ballistics: Theory and Design of Guns and Ammunition. Boca Raton, FL: CRC Press, 2007. ISBN 1420066188.
• Coriolis, G.G. "Mémoire sur le principe des forces vives dans les mouvements relatifs des machines." Journal de l'école Polytechnique 13 (1832): 268–302.
• Coriolis, G.G. "Mémoire sur les équations du mouvement relatif des systèmes de corps." Journal de l'école Polytechnique 15 (1835): 142–154.
• Durran, D.R. Is the Coriolis force really responsible for the inertial oscillation? Bulletin of the American Meteorological Society 74 (1993): 2179–2184. Retrieved May 4, 2020.
• Durran, D.R., and S.K. Domonkos. An apparatus for demonstrating the inertial oscillation. Bulletin of the American Meteorological Society 77 (1996): 557–559. Retrieved May 4, 2020.
• Ebenholtz, Sheldon M. Oculomotor Systems and Perception. Cambridge, UK: Cambridge University Press, 2001. ISBN 0521804590
• Ehrlich, Robert. Turning the World Inside Out and 174 Other Simple Physics Demonstrations. Princeton, NJ: Princeton University Press, 1990. ISBN 0691023956
• Gill, A.E. Atmosphere-Ocean dynamics. New York, NY: Academic Press, 1982. ISBN 0122835220
• Holton, James R. An Introduction to Dynamic Meteorology. Burlington, MA: Elsevier Academic Press, 2004. ISBN 0123540151.
• Kageyama, Akira, and Mamoru Hyodo. Eulerian derivation of the Coriolis force. arxiv.org. Retrieved May 4, 2020.
• Kantha, Lakshmi H., and Carol Anne Clayson. Numerical Models of Oceans and Oceanic Processes. London, UK: Academic Press, 2000. ISBN 0124340687
• Marion, Jerry B. 1970. Classical Dynamics of Particles and Systems. New York, NY: Academic Press. ISBN 0534408966
• Marshall, John, and R. Alan Plumb. Atmosphere, Ocean, and Climate Dynamics: An Introductory Text. London, UK: Academic Press, 2007. ISBN 0125586914
• Mather, George. Foundations of perception. Hove, UK: Taylor & Francis, 2006. ISBN 0863778356
• McCully, James Greig. Beyond the moon: A Conversational, Common Sense Guide to Understanding the Tides. Hackensack, NJ: World Scientific, 2006. ISBN 9812566430
• Menke, William, and Dallas Abbott. Geophysical Theory. New York, NY: Columbia University Press, 1990. ISBN 0231067925
• Morin, David. Introduction to classical mechanics: with problems and solutions. Cambridge, UK: Cambridge University Press, 2008. ISBN 0521876222
• Owen, George E. Fundamentals of Scientific Mathematics. New York, NY: Harper & Row; Mineola, NY: Dover Publications, 2003(original 1964). ISBN 0486428087
• Price, James F. A Coriolis tutorial. whoi.edu. Retrieved May 4, 2020.
• Symon, Keith. Mechanics. Reading, MA: Addison-Wesley, 1971.
• Tavel, Morton. Contemporary Physics and the Limits of Knowledge. New Brunswick, NJ: Rutgers University Press, 2002. ISBN 0813530776

Historical

• Grattan-Guinness, I., ed. 1994. Companion Encyclopedia of the History and Philosophy of the Mathematical Sciences, Vols. I and II. London, UK; New York, NY: Routledge.
• Khrgian, A. 1970. Meteorology—A Historical Survey, Vol. 1. Jerusalem, IL: Israel Program for Scientific Translations.
• Kuhn, T.S. 1977. The Essential Tension, Selected Studies in Scientific Tradition and Change. Chicago, IL: University of Chicago Press. ISBN 9780226458052.
• Kutzbach, G. 1979. The Thermal Theory of Cyclones. A History of Meteorological Thought in the Nineteenth Century. Boston, MA: Amer. Meteor. Soc. ISBN 9780933876484.

External links

All links retrieved January 7, 2024.

• The definition of the Coriolis effect from the Glossary of Meteorology.
• Coriolis Force - from ScienceWorld.
• Bad Coriolis. An article uncovering misinformation about the Coriolis effect. By Alistair B. Fraser, Emeritus Professor of Meteorology at Pennsylvania State University.
• NASA notes.

---

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Coriolis effect  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Coriolis effect"

Note: Some restrictions may apply to use of individual images which are separately licensed.