Gear

Spur gears found on a piece of farm equipment.

A gear is a wheel with teeth around its circumference, the purpose of the teeth being to mesh with similar teeth on another mechanical device—usually another gear wheel—so that force can be transmitted between the two devices in a direction tangential to their surfaces. A non-toothed wheel can transmit some tangential force but will slip if the force is large; teeth prevent slippage and allow the transmission of large forces.

A gear can mesh with any device having teeth compatible with the gear's teeth. Such devices include racks and other non-rotating devices; however, the most common situation is for a gear to be in mesh with another gear. In this case, rotation of one gear necessarily causes the other gear to rotate. In this manner, rotational motion can be transferred from one location to another (that is, from one shaft to another).

Although gears of equal diameter may be used simply to transmit rotation from one shaft to another, gears of unequal diameter are more useful because they offer a mechanical advantage: the rotational speed and torque (rotational force) of the second gear differ from that of the first. In this manner, gears provide a means of increasing or decreasing the rotational speed or torque.

General

Numerous nonferrous alloys, cast irons, powder-metallurgy and even plastics are used in the manufacture of gears. However, steels are most commonly used because of their high strength to weight ratio and low cost.

The smaller gear in a pair is often called the pinion; the larger is called the gear or the wheel.

Mechanical advantage

The interlocking of the teeth in a pair of meshing gears means that their circumferences necessarily move at the same rate of linear motion (eg., meters per second (m/s), or feet per minute (ft/min)). Since rotational speed (eg., measured in revolutions per second, revolutions per minute, or radians per second) is proportional to a wheel's circumferential speed divided by its radius, we see that the larger the radius of a gear, the slower will be its rotational speed, when meshed with a gear of given size and speed. The same conclusion can also be reached by a different analytical process: counting teeth. Since the teeth of two meshing gears are locked in a one to one correspondence, when all of the teeth of the smaller gear have passed the point where the gears meet – for example, when the smaller gear has made one revolution—not all of the teeth of the larger gear will have passed that point—the larger gear will have made less than one revolution. The smaller gear makes more revolutions in a given period of time; it turns faster. The speed ratio is simply the reciprocal ratio of the numbers of teeth on the two gears.

speed A : speed B   : :   number of teeth B : number of teeth A

This ratio is known as the gear ratio.

The torque ratio can be determined by considering the force that a tooth of one gear exerts on a tooth of the other gear. Consider two teeth in contact at a point on the line joining the shaft axes of the two gears. In general, the force will have both a radial and a circumferential component. The radial component can be ignored: it merely causes a sideways push on the shaft and does not contribute to turning. The circumferential component causes turning. The torque is equal to the circumferential component of the force times radius. Thus we see that the larger gear experiences greater torque; the smaller gear less. The torque ratio is equal to the ratio of the radii. This is exactly the inverse of the case with the velocity ratio. Higher torque implies lower velocity and vice versa. The fact that the torque ratio is the inverse of the velocity ratio could also be inferred from the law of conservation of energy. Here we have been neglecting the effect of friction on the torque ratio. The velocity ratio is truly given by the tooth or size ratio, but friction will cause the torque ratio to be actually somewhat less than the inverse of the velocity ratio.

In the above discussion we have made mention of the gear "radius." Since a gear is not a proper circle but a roughened circle, it does not have a radius. However, in a pair of meshing gears, each may be considered to have an effective radius, called the pitch radius, the pitch radii being such that smooth wheels of those radii would produce the same velocity ratio that the gears actually produce. The pitch radius can be considered sort of an "average" radius of the gear, somewhere between the outside radius of the gear and the radius at the base of the teeth.

The issue of pitch radius brings up the fact that the point on a gear tooth where it makes contact with a tooth on the mating gear varies during the time the pair of teeth are engaged; also the direction of force may vary. As a result, the velocity ratio (and torque ratio) is not, actually, in general, constant, if one considers the situation in detail, over the course of the period of engagement of a single pair of teeth. The velocity and torque ratios given at the beginning of this section are valid only "in bulk"—as long-term averages; the values at some particular position of the teeth may be different.

It is in fact possible to choose tooth shapes that will result in the velocity ratio also being absolutely constant—in the short term as well as the long term. In good quality gears this is usually done, since velocity ratio fluctuations cause undue vibration, and put additional stress on the teeth, which can cause tooth breakage under heavy loads at high speed. Constant velocity ratio may also be desirable for precision in instrumentation gearing, clocks and watches. The involute tooth shape is one that results in a constant velocity ratio, and is the most commonly used of such shapes today.

Tooth profile

The attainment of a non-fluctuating velocity ratio is dependent on the profile of the teeth. Friction and wear between two gears is also dependent on the tooth profile. There are a great many tooth profiles that will give a constant velocity ratio, and in many cases, given an arbitrary tooth shape, it is possible to develop a tooth profile for the mating gear that will give a constant velocity ratio. However, two constant velocity tooth profiles have been by far the most commonly used in modern times. They are the cycloid gear and the involute gear. The cycloid was more common until the late 1800s; since then the involute has largely superseded it, particularly in drive train applications. The cycloid is in some ways the more interesting and flexible shape; however the involute has two advantages: it is easier to manufacture, and it permits the center to center spacing of the gears to vary over some range without ruining the constancy of the velocity ratio. Cycloidal gears only work properly if the center spacing is exactly right. Cycloidal gears are still used in mechanical clocks.

Comparison with other drive mechanisms

The definite velocity ratio which results from having teeth gives gears an advantage over other drives (such as traction drives and V-belts) in precision machines such as watches that depend upon an exact velocity ratio. In cases where driver and follower are in close proximity gears also have an advantage over other drives in the reduced number of parts required; the downside is that gears are more expensive to manufacture and their lubrication requirements may impose a higher operating cost.

The automobile transmission allows selection between gears to give various mechanical advantages.

A gearbox is not an amplifier or a servomechanism. Conservation of energy requires that the amount of power delivered by the output gear or shaft will never exceed the power applied to the input gear, regardless of the gear ratio. Work equals the product of force and distance, therefore the small gear is required to run a longer distance and in the process is able to exert a larger twisting force or torque, than would have been the case if the gears were the same size. There is actually some loss of output power due to friction. With industrial quality gears made according to good commercial practice, and properly lubricated, the energy loss is usually two percent or less.

Intermeshing gears in motion.

Unlike most gears, an internal gear (shown here) does not cause direction reversal.

Spur gears

Spur gears are the simplest, and probably most common, type of gear. Their general form is a cylinder or disk (a disk is just a short cylinder). The teeth project radially, and with these "straight-cut gears," the leading edges of the teeth are aligned parallel to the axis of rotation. These gears can only mesh correctly if they are fitted to parallel axles.

Cage gear

The cage gear, also called lantern gear or lantern pinion, has been used for centuries. Its teeth are cylindrical rods, parallel to the axle and arranged in a circle around it, similar to the bars on a round bird cage or lantern. The assembly is held together by disks at either end into which the tooth rods and axle are set.

Helical gears

Helical gears from a Meccano construction set.

Helical gears offer a refinement over spur gears. The leading edges of the teeth are not parallel to the axis of rotation, but are set at an angle. Since the gear is curved, this angling causes the tooth shape to be a segment of a helix. The angled teeth engage more gradually than do spur gear teeth. This causes helical gears to run more smoothly and quietly than spur gears. Helical gears also offer the possibility of using non-parallel shafts. A pair of helical gears can be meshed in two ways: with shafts orientated at either the sum or the difference of the helix angles of the gears. These configurations are referred to as parallel or crossed, respectively. The parallel configuration is the more mechanically sound. In it, the helices of a pair of meshing teeth meet at a common tangent, and the contact between the tooth surfaces will, generally, be a curve extending some distance across their face widths. In the crossed configuration, the helices do not meet tangentially, and only point contact is achieved between tooth surfaces. Because of the small area of contact, crossed helical gears can only be used with light loads.

Quite commonly, helical gears come in pairs where the helix angle of one is the negative of the helix angle of the other; such a pair might also be referred to as having a right handed helix and a left handed helix of equal angles. If such a pair is meshed in the 'parallel' mode, the two equal but opposite angles add to zero: the angle between shafts is zero—that is, the shafts are parallel. If the pair is meshed in the 'crossed' mode, the angle between shafts will be twice the absolute value of either helix angle.

Note that 'parallel' helical gears need not have parallel shafts—this only occurs if their helix angles are equal but opposite. The 'parallel' in 'parallel helical gears' must refer, if anything, to the (quasi) parallelism of the teeth, not to the shaft orientation.

As mentioned at the start of this section, helical gears operate more smoothly than do spur gears. With parallel helical gears, each pair of teeth first make contact at a single point at one side of the gear wheel; a moving curve of contact then grows gradually across the tooth face. It may span the entire width of the tooth for a time. Finally, it recedes until the teeth break contact at a single point on the opposite side of the wheel. Thus force is taken up and released gradually. With spur gears, the situation is quite different. When a pair of teeth meet, they immediately make line contact across their entire width. This causes impact stress and noise.

Spur gears make a characteristic whine at high speeds and can not take as much torque as helical gears because their teeth are receiving impact blows. Whereas spur gears are used for low-speed applications and those situations where noise control is not a problem, the use of helical gears is indicated when the application involves high speeds, large power transmission, or where noise abatement is important. The speed is considered to be high when the pitch line velocity (that is, the circumferential velocity) exceeds 5000 (ft/min).

Disadvantages of helical gears include a resultant thrust along the axis of the gear, which needs to be accommodated by appropriate thrust bearings, and a greater degree of sliding friction between the meshing teeth, often addressed with specific additives in the lubricant.

Double helical gears

Double helical gears, invented by André Citroën and also known as herringbone gears, overcome the problem of axial thrust presented by single helical gears by having teeth that set in a 'V' shape. Each gear in a double helical gear can be thought of as two standard, but mirror image, helical gears stacked. This cancels out the thrust since each half of the gear thrusts in the opposite direction. They can be directly interchanged with spur gears without any need for different bearings.

Where the oppositely angled teeth meet in the middle of a herringbone gear, the alignment may be such that tooth tip meets tooth tip, or the alignment may be staggered, so that tooth tip meets tooth trough. The latter type of alignment results in what is known as a Wuest type herringbone gear.

With the older method of fabrication, herringbone gears had a central channel separating the two oppositely angled courses of teeth. This was necessary to permit the shaving tool to run out of the groove. The development of the Sykes gear shaper now makes it possible to have continuous teeth, with no central gap.

Bevel gears

Bevel gear used to lift floodgate by means of central screw.

Bevel gears are essentially conically shaped, although the actual gear does not extend all the way to the vertex (tip) of the cone that bounds it. With two bevel gears in mesh, the vertices of their two cones lie on a single point, and the shaft axes also intersect at that point. The angle between the shafts can be anything except zero or 180 degrees. Bevel gears with equal numbers of teeth and shaft axes at 90 degrees are called miter gears.

The teeth of a bevel gear may be straight-cut as with spur gears, or they may be cut in a variety of other shapes. 'Spiral bevel gears' have teeth that are both curved along their (the tooth's) length; and set at an angle, analogously to the way helical gear teeth are set at an angle compared to spur gear teeth. 'Zero bevel gears' have teeth which are curved along their length, but not angled. Spiral bevel gears have the same advantages and disadvantages relative to their straight-cut cousins as helical gears do to spur gears. Straight bevel gears are generally used only at speeds below 5 m/s (1000 ft/min), or, for small gears, 1000 revolutions per minute (rpm).

Crown gear

A crown gear

A crown gear (or contrate gear) is a particular form of bevel gear whose teeth project at right angles to the plane of the wheel; in their orientation the teeth resemble the points on a crown. A crown gear can only mesh accurately with another bevel gear, although crown gears are sometimes seen meshing with spur gears. A crown gear is also sometimes meshed with an escapement such as found in mechanical clocks.

Hypoid gears

Hypoid gears resemble spiral bevel gears, except that the shaft axes are offset, not intersecting. The pitch surfaces appear conical but, to compensate for the offset shaft, are in fact hyperboloids of revolution. Hypoid gears are almost always designed to operate with shafts at 90 degrees. Depending on which side the shaft is offset to, relative to the angling of the teeth, contact between hypoid gear teeth may be even smoother and more gradual than with spiral bevel gear teeth. Also, the pinion can be designed with fewer teeth than a spiral bevel pinion, with the result that gear ratios of 60:1 and higher are "entirely feasible" using a single set of hypoid gears.

Worm gear

A worm and gear from a Meccano construction set

A worm is a gear that resembles a screw. It is a species of helical gear, but its helix angle is usually somewhat large(for example, somewhat close to 90 degrees) and its body is usually fairly long in the axial direction; and it is these attributes which give it its screw like qualities. A worm is usually meshed with an ordinary looking, disk-shaped gear, which is called the "gear," the "wheel," the "worm gear," or the "worm wheel." The prime feature of a worm-and-gear set is that it allows the attainment of a high gear ratio with few parts, in a small space. Helical gears are, in practice, limited to gear ratios of 10:1 and under; worm gear sets commonly have gear ratios between 10:1 and 100:1, and occasionally 500:1. In worm-and-gear sets, because the worm's helix angle is large, the sliding action between teeth is considerable, and the resulting frictional loss causes the efficiency of the drive to be usually less than 90 percent, sometimes less than 50 percent.

The distinction between a worm and a helical gear is made when at least one tooth persists for a full 360 degree turn around the helix. If this occurs, it is a 'worm'; if not, it is a 'helical gear'. A worm may have as few as one tooth. If that tooth persists for several turns around the helix, the worm will appear, superficially, to have more than one tooth, but what one in fact sees is the same tooth reappearing at intervals along the length of the worm. The usual screw nomenclature applies: a one-toothed worm is called "single thread" or "single start"; a worm with more than one tooth is called "multiple thread" or "multiple start."

We should note that the helix angle of a worm is not usually specified. Instead, the lead angle, which is equal to 90 degrees minus the helix angle, is given.

In a worm-and-gear set, the worm can always drive the gear. However, if the gear attempts to drive the worm, it may or may not succeed. Particularly if the lead angle is small, the gear's teeth may simply lock against the worm's teeth, because the force component circumferential to the worm is not sufficient to overcome friction. Whether this will happen depends on a function of several parameters; however, an approximate rule is that if the tangent of the lead angle is greater than the coefficient of friction, the gear will not lock. Worm-and-gear sets that do lock in the above manner are called "self locking." The self locking feature can be an advantage, as for instance when it is desired to set the position of a mechanism by turning the worm and then have the mechanism hold that position. Tuning gears on stringed musical instruments work that way.

If the gear in a worm-and-gear set is an ordinary helical gear only point contact between teeth will be achieved. If medium to high power transmission is desired, the tooth shape of the gear is modified to achieve more intimate contact with the worm thread. A noticeable feature of most such gears is that the tooth tops are concave, so that the gear partly envelopes the worm. A further development is to make the worm concave (viewed from the side, perpendicular to its axis) so that it partly envelopes the gear as well; this is called a cone-drive or Hindley worm.

Sun and planet gear

Schematic animation of Watt's sun and planet gears. The Sun is yellow, the planet red, the reciprocating crank is blue, the flywheel is green and the driveshaft is gray. Notice that the sun and flywheel rotate twice for every rotation of the planet.

The sun and planet gear was a method of converting reciprocal motion to rotary motion, utilizing a reciprocating steam engine. It was likely invented by the Scottish engineer William Murdoch, an employee of Boulton and Watt, but was patented by James Watt in October 1781. It played an important part in the development of devices for rotative motion in the Industrial Revolution.

The sun and planet gear converted the vertical motion of a beam, driven by a small steam engine, into circular motion using a 'planet,' a cogwheel fixed at the end of the pumping rod (connected to the beam) of the engine. With the motion of the beam, this revolved around, and turned, the 'sun,' a larger rotating cog which turned the drive shaft, thus generating rotary motion. An interesting feature of this arrangement, when compared to that of a simple crank, is that when both sun and planet have the same number of teeth, the drive shaft completes two revolutions for each stroke of the beam and not a 1:1 ratio as expected.

Epicyclic gearing

In an ordinary gear train, the gears rotate but their axes are stationary. An epicyclic gear train is one in which one or more of the axes also moves. Examples are:

• The sun and planet gear system, in which the axis of the planet gear revolves around the central sun gear.
• The differential gear system used to drive the wheels of an automobile, in which the axis of the central bevel pinion is turned "end over end" by the ring gear, the drive to the wheels being taken off by bevel gears meshing with the central bevel pinion. With the differential gearing, the sum of the two wheel speeds is fixed, but how it is divided between the two wheels is undetermined, so the outer wheel can run faster and the inner wheel slower when turning corners.

Rack and pinion

Rack and pinion animation

A rack is a toothed bar or rod that can be thought of as a sector gear with an infinitely large radius of curvature. Torque can be converted to linear force by meshing a rack with a pinion: the pinion turns; the rack moves in a straight line. Such a mechanism is used in automobiles to convert the rotation of the steering wheel into the left-to-right motion of the tie rod(s). Racks also feature in the theory of gear geometry, where, for instance, the tooth shape of an interchangeable set of gears may be specified for the rack (infinite radius), and the tooth shapes for gears of particular actual radii then derived from that.

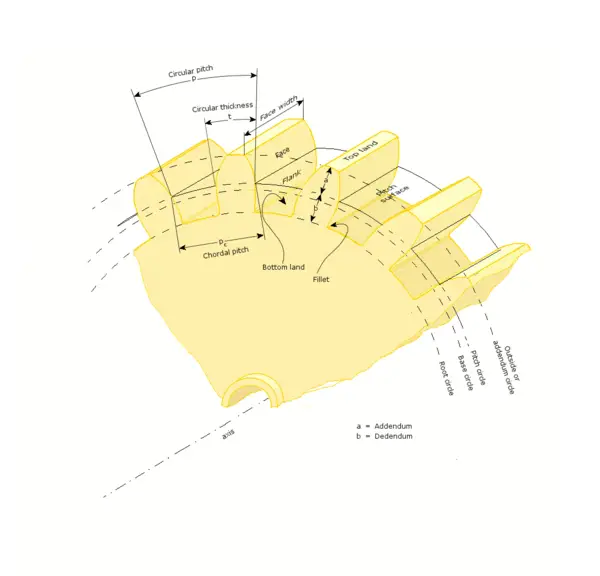
Gear nomenclature

• Common abbreviations
  • n.  Rotational velocity. (Measured, for example, in r.p.m.)
  • ω  Angular velocity. (Radians per unit time.) (1 r.p.m. = π/30 radians per second.)
  • N.  Number of teeth.
• 'Path of contact'. The path followed by the point of contact between two meshing gear teeth.
• 'Line of action', also called 'Pressure line'. The line along which the force between two meshing gear teeth is directed. It has the same direction as the force vector. In general, the line of action changes from moment to moment during the period of engagement of a pair of teeth. For involute gears, however, the tooth-to-tooth force is always directed along the same line—that is, the line of action is constant. this implies that for involute gears the path of contact is also a straight line, coincident with the line of action—as is indeed the case.
• 'Axis'. The axis of revolution of the gear; center line of the shaft.
• 'Pitch point' (p). The point where the line of action crosses a line joining the two gear axes.
• 'Pitch circle'. A circle, centered on and perpendicular to the axis, and passing through the pitch point. Sometimes also called the 'pitch line', although it is a circle.
• 'Pitch diameter' (D). Diameter of a pitch circle. Equal to twice the perpendicular distance from the axis to the pitch point. The nominal gear size is usually the pitch diameter.
• 'Pitch surface'. For cylindrical gears, this is the cylinder formed by projecting a pitch circle in the axial direction. More generally, it is the surface formed by the sum of all the pitch circles as one moves along the axis. E.g., for bevel gears it is a cone.
• 'Angle of action'. Angle with vertex at the gear center, one leg on the point where mating teeth first make contact, the other leg on the point where they disengage.
• 'Arc of action'. The segment of a pitch circle subtended by the angle of action.
• 'Pressure angle' (ø). The complement of the angle between the direction that the teeth exert force on each other, and the line joining the centers of the two gears. For involute gears, the teeth always exert force along the line of action, which, for involute gears, is a straight line; and thus, for involute gears, the pressure angle is constant.
• 'Outside diameter' (D_o). Distance from the gear center to the tops of the teeth.
• 'Root diameter'. Distance from the gear center to the bottoms of the troughs between teeth.
• 'Addendum' (a). The radial distance from the pitch surface to the outermost point of the tooth.  a = D_o - D.
• 'Dedendum' (b). The radial distance from the depth of the tooth trough to the pitch surface. b = D - root diameter.
• 'Whole depth' (h_t). Addendum plus dedendum; or, equivalently, outside diameter minus root diameter.
• 'Clearance'. The amount by which the dedendum of a gear exceeds the addendum of the gear it is mating with.
• 'Working depth'. The depth of engagement of two gears. It equals the sum of their addenda.
• 'Circular pitch' (p). The distance from one face of a tooth to the corresponding face of an adjacent tooth on the same gear, measured along the pitch circle.
• 'Diametral pitch' (P_d). The ratio of the number of teeth to the pitch diameter. E.g., could be measured in teeth per inch or teeth per centimeter.
• 'Base circle'. Applies only to involute gears, where the tooth profile is the involute of the base circle. The radius of the base circle is somewhat smaller than that of the pitch circle.
• Base pitch (p_b). Applies only to involute gears. It is the distance from one face of a tooth to the corresponding face of an adjacent tooth on the same gear, measured along the base circle. Sometimes called the 'normal pitch'.
• 'Interference'. Contact between teeth other than at the intended parts of their surfaces.
• 'Interchangeable set'. A set of gears, any of which will mate properly with any other.
• Helical Gears:
  • 'Helix angle' (ψ). The angle between a tangent to the helix and the gear axis. Is zero in the limiting case of a spur gear.
  • 'Normal circular pitch' (p_n). Circular pitch in the plane normal to the teeth.
  • 'Transverse circular pitch' (p). Circular pitch in the plane of rotation of the gear. Sometimes just called "circular pitch." p_n = p cos(ψ).
  • Several other helix parameters can be viewed either in the normal or transverse planes. The subscript " _n " usually indicates the normal.
• Worm gears:
  • 'Lead'. The distance from any point on a thread to the corresponding point on the next turn of the same thread, measured parallel to the axis.
  • 'Linear pitch' (p). The distance from any point on a thread to the corresponding point on the adjacent thread, measured parallel to the axis. For a single-thread worm, lead and linear pitch are the same.
  • 'Lead angle' (λ). The angle between a tangent to the helix and a plane perpendicular to the axis. Note that it is the complement of the helix angle which isusually given for helical gears.
  • 'Pitch diameter' (D_w). Same as described earlier in this list. Note that for a worm it is still measured in a plane perpendicular to the gear axis, not a tilted plane.
  • Subscipt " _w " denotes the worm, " _g " denotes the gear.

Backlash

Backlash is the error in motion that occurs when gears change direction. It exists because there is always some gap between the tailing face of the driving tooth and the leading face of the tooth behind it on the driven gear, and that gap must be closed before force can be transferred in the new direction. The term "backlash" can also be used to refer to the size of the gap, not just the phenomenon it causes; thus, one could speak of a pair of gears as having, for example, "0.1 mm of backlash." A pair of gears could be designed to have zero backlash, but this would presuppose perfection in manufacturing, uniform thermal expansion characteristics throughout the system, and no lubricant. Therefore, gear pairs are designed to have some backlash. It is usually provided by reducing the tooth thickness of each gear by half the desired gap distance. In the case of a large gear and a small pinion, however, the backlash is usually taken entirely off the gear and the pinion is given full sized teeth. Backlash can also be provided by moving the gears farther apart.

For those situations (such as instrumentation and control) where precision is important, backlash can be minimized through one of several techniques. For instance, the gear can be split along a plane perpendicular to the axis, one half fixed to the shaft in the usual manner, the other half placed alongside it, free to rotate about the shaft, but with springs between the two halves providing relative torque between them, so that one achieves, in effect, a single gear with expanding teeth. Another method involves tapering the teeth in the axial direction and providing for the gear to be slid in the axial direction to take up slack.

Shifting of gears

In some machines (such as automobiles), it is necessary to change the gear ratio to suit the task. There are several ways of doing this. For example:

• Manual transmission
• Automatic transmission
• Derailleur gears, which are actually sprockets in combination with a roller chain
• Hub gears (also called epicyclic gearing or sun-and-planet gears)
• Continuously variable transmission
• Transmission (mechanics)

See also

• Automobile
• Bicycle
• Machine

References

ISBN links support NWE through referral fees

• Buckingham, Earle. Analytical Mechanics of Gears. Dover Publications, 2011 (original 1988). ISBN 0486657124.
• Doughtie, Venton Levy, and Alex Vallance. Design of Machine Members, 4th ed. New York: McGraw-Hill, 1964. ISBN 0070176353.
• Dudley, Darle W. Handbook of Practical Gear Design. Boca Raton, FL: CRC Press, 1994. ISBN 1566762182.
• Horton, Holbrook, and Earle Buckingham. Manual of Gear Design Vol. 1-3 New York: Industrial Press, 1999 (original 1981). ISBN 0831131160.
• Jones, Franklin. Gear Design Simplified, 3rd ed. New York: Industrial Press, 1984 (original 1961). ISBN 0831111593.
• McGraw-Hill Encyclopedia of Science and Technology. New York: McGraw-Hill, 2002. ISBN 0079136656.

External links

All links retrieved April 18, 2024.

• Mathematical Tutorial for Gearing (Relating to Robotics)
• Animation of an Involute Rack and Pinion

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Gear  ^history
• Sun_and_planet_gear  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Gear"

Note: Some restrictions may apply to use of individual images which are separately licensed.