Celestial sphere

The celestial sphere is divided by the celestial equator.

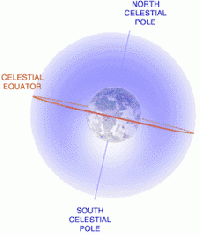
In its modern sense, as used in astronomy and navigation, the celestial sphere is an imaginary rotating sphere of gigantic radius, concentric and coaxial with the Earth. All objects in the sky can be thought of as lying upon the sphere. Projected from their corresponding geographic equivalents are the celestial equator and the celestial poles. The celestial sphere projection is a very practical tool for positional astronomy.

In the Aristotelic and Ptolemaic models, the celestial sphere was thought of as a physical reality rather than a geometrical projection.

A celestial sphere can also refer to a physical model of the celestial sphere. Also known as a star globe, this sort of celestial sphere will indicate which constellations are visible at a given time and place.

Characteristics

The celestial sphere can be used geocentrically and topocentrically. The former means that it is centered on an imaginary observer in the center of the Earth, and no parallax effects need to be taken into account. In the latter case, it is centered on an observer on the surface of the Earth and then horizontal parallax cannot always be ignored; especially not for the Moon.

The celestial sphere is divided by projecting the equator into space. This divides the sphere into the north celestial hemisphere and the south celestial hemisphere. Likewise, one can locate the Celestial Tropic of Cancer, Celestial Tropic of Capricorn, North Celestial Pole, and South Celestial Pole. The directions toward various objects in the sky can be quantified by constructing a celestial coordinate system.

As the Earth rotates from west to east around its axis once every 23 hours 56 minutes, the celestial sphere and all objects on it appear to rotate from east to west around the celestial poles in the same time. This is the diurnal motion. Therefore stars will rise in the east, culminate on the north-south line (meridian) and set in the west, (unless a star is circumpolar). On the next night a particular star will rise again, but with our normal clocks running a 24 hour 0 minutes cycle, it will do so 4 minutes earlier. By the following night the difference will be 8 minutes, and so forth with every following night (or day).

The reason for this apparent misadjustment of our clocks is that the Sun is not standing still on the celestial sphere, as the stars do, but moves about 1° per day eastwards over a great circle known as the ecliptic (which is 360° or a full circle in one year, the annual motion of the Sun). As an angle of 1° corresponds to 4 minutes in time (360° = 24 hours), we need therefore 4 extra minutes of diurnal motion to see the Sun back on (for example) the meridian again, making the duration of one rotation just 24 hours exactly (on the average, ignoring small seasonal variations, see equation of time)

Normal clocks therefore indicate solar time. Astronomers studying the movements of stars may want clocks indicating sidereal time, going around once in 23h56m (solar time units).

Celestial spheres from Antiquity to the Renaissance

Geocentric celestial spheres; Peter Apian's Cosmographia (Antwerp, 1539).

Thomas Digges' 1576 Copernican heliocentric model of the celestial orbs.

The celestial spheres, or celestial orbs, were the fundamental celestial entities of the cosmological celestial mechanics first invented by Eudoxus, and developed by Aristotle, Ptolemy, Copernicus and others. In this celestial model the stars and planets are carried around by being embedded in rotating spheres made of an aetherial transparent fifth element (quintessence), like jewels set in orbs.

In geocentric models the spheres were most commonly arranged outwards from the centre in this order: the sphere of the Moon, the sphere of Mercury, the sphere of Venus, the sphere of the Sun, the sphere of Mars, the sphere of Jupiter, the sphere of Saturn, the starry firmament, and sometimes one or two additional spheres. The order of the lower planets was not universally agreed. Plato and his followers ordered them Moon, Sun, Mercury, Venus, and then followed the standard model for the upper spheres. Others disagreed about the relative place of the spheres of Mercury and Venus: Ptolemy placed both of them beneath the Sun and with Venus beneath Mercury, but noted others placed them both above the Sun, and some even on either side of the Sun, as Alpetragius came to do.

In the heliocentric celestial orbs model introduced by Copernicus, the ascending order of the planets and their spheres going outwards from the Sun at the centre was Mercury, Venus, Earth-Moon, Mars, Jupiter and Saturn.

History

Antiquity

In his Metaphysics, Aristotle adopted and developed a celestial physics of uniformly rotating geo-concentric nested spheres first devised and developed by the astronomers Eudoxus and Callippus. In Aristotle's fully developed celestial mechanics, the spherical Earth is at the centre of the universe and the planets and stars are moved by either 48 or 56 completely interconnected spheres altogether, whereas in the models of Eudoxus and Callippus each planet's individual set of spheres were not connected to those of the next planet. Each planet is attached to the innermost of its own particular set of spheres. Aristotle considers that these spheres are made of an unchanging fifth element, the aether. Each of these concentric spheres is moved by its own god—an unchanging divine unmoved mover, and who moves its sphere simply by virtue of being loved by it.Aristotle says the exact number of spheres is to be determined by astronomical investigation, but he disagreed with the numbers imputed by the contemporary astronomers Eudoxus and Callippus, adding many more. The exact number of divine unmoved movers is to be determined by metaphysics, and Aristotle assigned one unmoved mover per sphere.

Ptolemaic model of the spheres for Venus, Mars, Jupiter, and Saturn with epicycle, eccentric deferent and equant point. Georg von Peuerbach, Theoricae novae planetarum, 1474.

The astronomer Ptolemy (fl. ca. 150 C.E.) defined a geometrical model of the universe in his Almagest and extended it to a physical model of the cosmos in his Planetary hypotheses. In doing so, he achieved greater mathematical detail and predictive accuracy that had been lacking in earlier spherical models of the cosmos. In the Ptolemaic model, each planet is moved by two or more spheres, but in Book 2 of his Planetary Hypotheses Ptolemy depicted circular bands as in Plato’s Timaeus model rather than spheres as in its Book 1. One sphere/band is the deferent, with a centre offset somewhat from the Earth; the other sphere/band is an epicycle embedded in the deferent, with the planet embedded in the epicyclical sphere/band. In the case of the bands or rings model, Ptolemy likened it to a tambourine in which the epicyclical disc is like the jingles or zils fixed in its circumference, the deferent.

Middle Ages

Christian and Muslim philosophers modified Ptolemy's system to include an unmoved outermost region, which was the dwelling place of God and all the elect. The outermost moving sphere, which moved with the daily motion affecting all subordinate spheres, was moved by a fixed unmoved mover, the Prime Mover, who was identified with God. Each of the lower spheres was moved by a subordinate spiritual mover (a replacement for Aristotle's multiple divine movers), called an intelligence.

Around the turn of the millennium, the Arabian astronomer and polymath Ibn al-Haytham (Alhacen) presented a development of Ptolemy's geocentric epicyclic models in terms of nested spheres. Despite the similarity of this concept to that of Ptolemy's Planetary Hypotheses, al-Haytham's presentation differs in sufficient detail that it has been argued that it reflects an independent development of the concept. In chapters 15-16 of his Book of Optics, Ibn al-Haytham also discovered that the celestial spheres do not consist of solid matter.

Near the end of the twelfth century, the Spanish-Arabian Muslim astronomer al-Bitrūjī (Alpetragius) sought to explain the complex motions of the planets using purely concentric spheres, which moved with differing speeds from east to west. This model was an attempt to restore the concentric spheres of Aristotle without Ptolemy's epicycles and eccentrics, but it was much less accurate as a predictive astronomical model.

In the thirteenth century, scholars in European universities dealt with the implications of the rediscovered philosophy of Aristotle and astronomy of Ptolemy. One issue that arose concerned the nature of the celestial spheres. Through an extensive examination of a wide range of scholastic texts, Edward Grant has demonstrated that scholastic philosophers generally considered the celestial spheres to be solid in the sense of three-dimensional or continuous, but most did not consider them solid in the sense of hard. The consensus was that the celestial spheres were made of some kind of continuous fluid.

The dynamics of the celestial spheres

- Inertia in the celestial spheres

However, the motions of the celestial spheres came to be seen as presenting a major anomaly for Aristotelian dynamics, and as even refuting its general law of motion v α F/R. According to this law all motion is the product of a motive force (F) and some resistance to motion (R), and whose ratio determines its average speed (v). And the ancestor of the central concept of Newtonian dynamics, the concept of the force of inertia as an inherent resistance to motion in all bodies, was born out of attempts to resolve it. This problem of celestial motion for Aristotelian dynamics arose as follows.

In Aristotle's sublunar dynamics all motion is either 'natural' or 'violent'. Natural motion is motion driven solely by the body's own internal 'nature' or gravity (or levity), that is, a centripetal tendency to move straight downward towards their natural place at the centre of the Earth (and universe) and to be at rest there. And its contrary, violent motion, is simply motion in any other direction whatever, including motion along the horizontal. Any such motion is resisted by the body's own 'nature' or gravity, thus being essentially anti-gravitational motion.

Hence gravity is the driver of natural motion, but a brake on violent motion, or as Aristotle put it, a 'principle of both motion and rest'. And gravitational resistance to motion is virtually omni-directional, whereby in effect bodies have horizontal 'weight' as well as vertically downward weight.The former consists of a tendency to be at rest and resist motion along the horizontal wherever the body may be on it (technically termed an inclinatio ad quietem in scholastic dynamics, as distinct from its tendency to centripetal motion as downwards weight that resists upward motion (technically termed an inclinatio ad contraria in scholastic dynamics).

The only two resistances to sublunar motion Aristotle identified were this gravitational internal resistance just to violent motion, measured by the body's weight, and more generally in both natural and violent motion also the external resistance of the medium of motion to being cleaved by the mobile in the sublunar plenum, measured by the density of the medium.

Thus Aristotle's general law of motion assumed two different interpretations for the two different dynamical cases of natural and violent sublunar motion. In the case of sublunar natural motion the general law v α F/R becomes v α W/R (because Weight is the measure of the motive force of gravity), with the body's motion driven by its weight and resisted by the medium.But in the case of violent motion the general law v α F/R then becomes v α F/W because the body's weight now acts as a resistance that resists the violent mover F, whatever that might be, such as a hand pulling a weight up from the floor or a gang of ship-hauliers hauling a ship along the shore or a canal.

However, in Aristotle's celestial physics, whilst the spheres have movers, each being 'pushed' around by its own soul seeking the love of its own god as its unmoved mover, whereby F > 0, there is no resistance to their motion whatever, since Aristotle's quintessence has neither gravity nor levity, whereby they have no internal resistance to their motion. And nor is there any external resistance such as any resistant medium to be cut through, whereby altogether R = 0. Yet in dynamically similar terrestrial motion, such as in the hypothetical case of gravitational fall in a vacuum,driven by gravity (i.e. F = W > 0), but without any resistant medium (i.e. R = 0), Aristotle's law of motion therefore predicts it would be infinitely fast or instantaneous, since then v α W/R = W/0 = infinite.

But in spite of these very same dynamical conditions of celestial bodies having movers but no resistance to them, in the heavens even the fastest sphere of all, the stellar sphere, apparently took 24 hours to rotate, rather than being infinitely fast or instantaneous as Aristotle's law predicted sublunar gravitational free-fall would be.

Thus when interpreted as a cosmologically universal law, Aristotle's basic law of motion was cosmologically refuted by his own dynamical model of celestial natural motion as a driven motion that has no resistance to it.

Hence in the sixth century, John Philoponus argued that the finite speed rotation of the celestial spheres empirically refuted Aristotle's thesis that natural motion would be instantaneous in a vacuum where there is no medium the mobile has to cut through, as follows:

"For if in general the reason why motion takes time were the physical [medium] that is cut through in the course of this motion, and for this reason things that moved through a vacuum would have to move without taking time because of there being nothing for them to cut through, this ought to happen all the more in the case of the fastest of all motions, I mean the [celestial] rotation. For what rotates does not cut through any physical [medium] either. But in fact this [timeless motion] does not happen. All rotation takes time, even without there being anything to cut through in the motion."

Consequently Philoponus sought to resolve this devastating celestial empirical refutation of Aristotelian mathematical dynamics by Aristotle's own rotating celestial spheres by rejecting Aristotle's core law of motion and replacing it with the alternative law v α F - R, whereby a finite force does not produce an infinite speed when R = 0. The essential logic of this refutation of Aristotle's law of motion can be reconstructed as follows. The prediction of the speed of the spheres' rotations in Aristotelian celestial dynamics is given by the following logical argument

[ (i) v α F/R & (ii) F > 0 & (iii) R = 0 ] entail v is infinite.

These premises comprise the conjunction of Aristotle's law of motion in premise (i) with his dynamical model of celestial motion expressed in premises (ii) & (iii). But the contrary observation v is not infinite entails at least one premise of this conjunction must be false. But which one ?

Philoponus decided to direct the falsifying logical arrow of modus tollens at the very first of the three theoretical premises of this prediction, namely Aristotle's law of motion, and replace it with his alternative law v α F - R. But logically premises (ii) or (iii) could have been rejected and replaced instead. And indeed some six centuries later premise (iii) was rejected and replaced.

For in the twelfth century Averroes rejected Philoponus's 'anti-Aristotelian' solution to this refutation of Aristotelian celestial dynamics that had rejected its core law of motion v α F/R. Instead he restored Aristotle's law of motion as premise (i) by adopting the 'hidden variable' approach to resolving apparent refutations of parametric laws that posits a previously unaccounted variable and its value(s) for some parameter, thereby modifying the predicted value of the subject variable, in this case the average speed of motion v. For he posited there was a non-gravitational previously unaccounted inherent resistance to motion hidden within the celestial spheres. This was a non-gravitational inherent resistance to motion of superlunary quintessential matter, whereby R > 0 even when there is neither any gravitational nor any media resistance to motion.

Hence the alternative logic of Averroes' solution to the refutation of the prediction of Aristotelian celestial dynamics

[ (i) v α F/R & (ii) F > 0 & (iii) R = 0 ] entail v is infinite

was to reject its third premise R = 0 instead of rejecting its first premise as Philoponus had, and assert R > 0.

Thus Averroes most significantly revised Aristotle's law of motion v α F/R into v α F/M for the case of celestial motion with his auxiliary theory of what may be called celestial inertia M, whereby R = M > 0. But Averroes restricted inertia to celestial bodies and denied sublunar bodies have any inherent resistance to motion other than their gravitational (or levitational) inherent resistance to violent motion, just as in Aristotle's original sublunar physics.

However, Averroes’ thirteenth century follower Thomas Aquinas accepted Averroes' theory of celestial inertia, but rejected his denial of sublunar inertia, and extended Averroes' innovation in the celestial physics of the spheres to all sublunar bodies. He posited all bodies universally have a non-gravitational inherent resistance to motion constituted by their magnitude or mass. In his Systeme du Monde the pioneering historian of medieval science Pierre Duhem said of Aquinas' innovation:

"For the first time we have seen human reason distinguish two elements in a heavy body: the motive force, that is, in modern terms, the weight; and the moved thing, the corpus quantum, or as we say today, the mass. For the first time we have seen the notion of mass being introduced in mechanics, and being introduced as equivalent to what remains in a body when one has suppressed all forms in order to leave only the prime matter quantified by its determined dimensions. Saint Thomas Aquinas's analysis, completing Ibn Bajja's, came to distinguish three notions in a falling body: the weight, the mass, and the resistance of the medium, about which physics will reason during the modern era…. This mass, this quantified body, resists the motor attempting to transport it from one place to another, stated Thomas Aquinas."

Aquinas thereby predicted this non-gravitational inherent resistance to motion of all bodies would also prevent an infinite speed of gravitational free-fall for sub-lunar bodies as otherwise predicted by Aristotle's law of motion applied to pre-inertial Aristotelian dynamics in Aristotle's famous Physics 4.8.215a25f argument for the impossibility of natural motion in a vacuum i.e. of gravitational free-fall. Thus by eliminating the prediction of its infinite speed, Aquinas made gravitational fall in a vacuum dynamically possible in an alternative way to that in which Philoponus had rendered it theoretically possible.

Another logical consequence of Aquinas's theory of inertia was that all bodies would fall with the same speed in a vacuum because the ratio between their weight, i.e. the motive force, and their mass which resists it, is always the same. Or in other words in the Aristotelian law of average speed v α W/m, W/m = 1 and so v = k, a constant. But it seems the first known published recognition of this consequence of the Thomist theory of inertia was in the early fifteenth century by Paul of Venice in his critical exposition on Aristotle's Physics, in which he argued equal speeds of unequal weights in natural motion in a vacuum was not an absurdity and thus a reductio ad absurdum against the very possibility of natural motion in a vacuum as follows:

"It is not absurd that two unequal weights move with equal speed in the void; there is, in fact, no resistance other than the intrinsic resistance due to the application of the motor to the mobile, in order that its natural movement be accomplished. And the proportion of the motor to the mobile, with respect to the heavier body and the lighter body, is the same. They would then move with the same speed in the void. In the plenum, on the other hand, they would move with unequal speed because the medium would prevent the mobile from taking its natural movement."

As Duhem commented, this "glimpses what we, from the time of Newton, have expressed as follows: Unequal weights fall with the same speed in the void because the proportion between their weight and their mass has the same value." But the first mention of a way of empirically testing this novel prediction of this Thomist revision of Aristotelian dynamics seems to be that detailed in the First Day of Galileo's 1638 Discorsi, namely by comparing the pendulum motions in air of two bobs of the same size but different weights.

However, yet another consequence of Aquinas's innovation in Aristotelian dynamics was that it contradicted its original law of interminable rest or locomotion in a void that an externally unforced body in motion in a void without gravity or any other resistance to motion would either remain at rest forever or if moving continue moving forever.For any such motion would now be terminated or prevented by the body's own internal resistance to motion posited by Aquinas, just as projectile violent motion against the countervailing resistance of gravity was impossible in a vacuum for Aristotle. Hence by the same token that Aquinas's theory of inertia predicted gravitational fall in a vacuum would not be infinitely fast, contra Aristotle's Physics 4.8.215a25f, so it also predicted there would not be interminable locomotion in a gravity-free void, in which any locomotion would terminate, contrary to Aristotle's Physics 4.8.215a19-22 and Newton's first law of motion.

Some five centuries after Averroes' and Aquinas's innovation, it was Kepler who first dubbed this non-gravitational inherent resistance to motion in all bodies universally 'inertia'. Hence the crucial notion of seventeenth century early classical mechanics of a resistant force of inertia inherent in all bodies was born in the heavens of medieval astrophysics, in the Aristotelian physics of the celestial spheres, rather than in terrestrial physics or in experiments.

This auxiliary theory of Aristotelian dynamics, originally devised to account for the otherwise anomalous finite speed rotations of the celestial spheres for Aristotle's law of motion, was a most important conceptual development in physics and Aristotelian dynamics in its second millennium of progress in the dialectical evolutionary transformation of its core law of motion into the basic law of motion of classical mechanics a α (F - R)/m. For it provided what was eventually to become that law's denominator, whereby when there is no other resistance to motion, the acceleration produced by a motive force is still not infinite by virtue of the inherent resistant force of inertia m. Its first millennium had seen Philoponus's 6th century innovation of net force in which those forces of resistance by which the motive force was to be divided in Aristotle's dynamics (e.g. media resistance and gravity) were rather to be subtracted instead to give the net motive force, thus providing what was eventually to become the numerator of net force F - R in the classical mechanics law of motion.

The first millennium had also seen the Hipparchan innovation in Aristotelian dynamics of its auxiliary theory of a self-dissipating impressed force or impetus to explain the sublunar phenomenon of detached violent motion such as projectile motion against gravity, which Philoponus had also applied to celestial motion. The second millennium then saw a radically different impetus theory of an essentially self-conserving impetus developed by Avicenna and Buridan which was also applied to celestial motion to provide what seems to have been the first non-animistic explanation of the continuing celestial motions once initiated by God.

- Impetus in the celestial spheres

In the fourteenth century the logician and natural philosopher Jean Buridan, Rector of Paris University, subscribed to the Avicennan variant of Aristotelian impetus dynamics according to which impetus is conserved forever in the absence of any resistance to motion, rather than being evanescent and self-decaying as in the Hipparchan variant. In order to dispense with the need for positing continually moving intelligences or souls in the celestial spheres, which he pointed out are not posited by the Bible, Buridan applied the Avicennan self-conserving impetus theory to their endless rotation by extension of a terrestrial example of its application to rotary motion in the form of a rotating millwheel that continues rotating for a long time after the originally propelling hand is withdrawn, driven by the impetus impressed within it.

Earlier Franciscus de Marchia had given a 'part impetus dynamics - part animistic' account of celestial motion in the form of the sphere’s angel continually impressing impetus in its sphere whereby it was moved directly by impetus and only indirectly by its moving angel. This hybrid mechanico-animistic explanation was necessitated by the fact that de Marchia only subscribed to the Hipparchan-Philoponan impetus theory in which impetus is self-dissipating rather than self-conserving, and thus would not last forever but need constant renewal even in the absence of any resistance to motion.

But Buridan attributed the cause of the continuing motion of the spheres wholly to impetus as follows:

"God, when He created the world, moved each of the celestial orbs as He pleased, and in moving them he impressed in them impetuses which moved them without his having to move them any more...And those impetuses which he impressed in the celestial bodies were not decreased or corrupted afterwards, because there was no inclination of the celestial bodies for other movements. Nor was there resistance which would be corruptive or repressive of that impetus."

However, having discounted the possibility of any resistance due to a contrary inclination to move in any opposite direction or due to any external resistance, in concluding their impetus was therefore not corrupted by any resistance Buridan also discounted any inherent resistance to motion in the form of an inclination to rest within the spheres themselves, such as the inertia posited by Averroes and Aquinas. For otherwise that resistance would destroy their impetus, as the anti-Duhemian historian of science Annaliese Maier maintained the Parisian impetus dynamicists were forced to conclude because of their belief in an inherent inclinatio ad quietem (tendency to rest) or inertia in all bodies. But in fact contrary to that inertial variant of Aristotelian dynamics, according to Buridan prime matter does not resist motion. ) But this then raised the question within Aristotelian dynamics of why the motive force of impetus does not therefore move the spheres with infinite speed. One impetus dynamics answer seemed to be that it was a secondary kind of motive force that produced uniform motion rather than infinite speed, just as it seemed Aristotle had supposed the spheres' moving souls do, or rather than uniformly accelerated motion like the primary force of gravity did by producing constantly increasing amounts of impetus.

However in his Treatise on the heavens and the world in which the heavens are moved by inanimate inherent mechanical forces, Buridan's pupil Oresme offered an alternative Thomist response to this problem in that he did posit a resistance to motion inherent in the heavens (i.e. in the spheres), but which is only a resistance to acceleration beyond their natural speed, rather than to motion itself, and was thus a tendency to preserve their natural speed. This analysis of the dynamics of the motions of the spheres seems to have been a first anticipation of Newton's subsequent more generally revised conception of inertia as resisting accelerated motion but not uniform motion.

Renaissance

Paul Wittich's 1578 Capellan geoheliocentric planetary model in which the Martian and Solar orbits do not intersect.

Early in the sixteenth century, Nicolaus Copernicus drastically reformed the model of astronomy by displacing the Earth from its central place in favor of the sun, yet he called his great work De revolutionibus orbium coelestium (On the Revolutions of the Celestial Spheres). Although Copernicus does not treat the physical nature of the spheres in detail, his few allusions make it clear that, like many of his predecessors, he accepted non-solid celestial spheres.

However, it seems a crucial physical reason for his heliocentrism in order to save the celestial spheres may have been that he rejected the possibility of interpenetrating spheres, but for some reason thought Martian parallax at opposition is greater than solar parallax, whereby Mars must then be nearer the Earth than the sun is, but also whereby the Martian and solar spheres must intersect on all geocentric and geoheliocentric planetary models. They can only be non-intersecting with Mars less than 1 AU away at opposition in the pure heliocentric model.

As Copernicus's pupil and herald Rheticus expressed this in his 1540 Copernican Narratio Prima, published three years before Copernicus's De Revolutionibus,

"Mars unquestionably shows a parallax sometimes greater than the sun's, and therefore it seems impossible that the earth should occupy the centre of the universe.".

But this is only an impossibility for a spherist cosmology in which different planetary spheres cannot intersect,but not for non-spherist astronomy, as illustrated by the non-spherist Tychonic geocentric model, for example, in which the Martian and solar orbits intersect (as also do the orbits of Mercury and Venus with those of Mars and of Jupiter as drawn).

Tycho Brahe's 1587 geoheliocentric planetary model in which the Martian and Solar orbits intersect.

Although Martian parallax at its maximum of some 23 arcseconds is indeed greater than the sun's at some 9 arcseconds, such differences are thought to have been instrumentally observationally indiscernible at that time before telescopes and micrometers, when the maximum discernible resolution by human naked eye observation is reckoned to be no more than some 30 arcseconds. Moreover at the time the traditionally accepted value for solar parallax, even by Tycho Brahe, was some 3 arcminutes.

This all raises the question of the basis on which astronomers compared Martian and solar parallax and what the consensus in the 16th century was, if any, on which is greater. The (geoheliocentric) planetary models of such as Paul Wittich and Nicolaus Reimers(aka Ursus) supposed that of Mars was never greater, whereas those of Copernicus and Tycho supposed it was greater at opposition. This all seems to imply disagreement in the 16th century about the observational facts of Martian parallax, but about which crucial issue the history of science literature is silent.

Yet it seems it was a firm belief in the greater oppositional parallax of Mars within geocentrism that undermined belief in the solid celestial spheres as physically possible because of the intersecting spheres problem, to which the only pro-spherist solution was pure heliocentrism. But heliocentrism was observationally 'refuted' by the apparent lack of any annual stellar parallax. Thus Tycho's view that heliocentrism was observationally refuted by the fact of no discernible stellar parallax enforced his rejection of solid spheres to sustain his observationally unjustified belief that Mars was less than 1 AU from the Earth at opposition. But his rejection of the spheres was at least observationally buttressed by his observations of the 1577 comet.

Ursus's 1588 geoheliocentric planetary model in which the Martian and Solar orbits do not intersect.

Tycho Brahe's observations that the comet of 1577 displayed less daily parallax than the Moon implied it was superlunary and so, impossibly, must pass through some planetary orbs in its transit. This led him to conclude that "the structure of the heavens was very fluid and simple."

Tycho opposed his view to that of "very many modern philosophers" who divided the heavens into "various orbs made of hard and impervious matter." Since Grant has been unable to identify such a large number of believers in hard celestial spheres before Copernicus, he concludes that the idea first became dominant sometime after the publication of Copernicus's De revolutionibus in 1542 and either before, or possibly somewhat after, Tycho Brahe's publication of his cometary observations in 1588.

In Johannes Kepler's celestial physics the spheres were regarded as the purely geometrical spatial regions containing each planetary orbit rather than physical bodies as rotating orbs as in preceding Aristotelian celestial physics. The eccentricity of each planet's elliptical orbit and its major and minor axes thereby defined the lengths of the radii of the inner and outer limits of its celestial sphere and thus its thickness. The intermediate causal role of these geometrical spherical shells in Kepler's Platonist geometrical cosmology is to determine the sizes and orderings of the five Platonic polyhedra within which the spheres were supposedly spatially embedded.

Thus in Kepler's celestial mechanics the previous ultimate causal role of the spheres became a non-ultimate intermediate role as the ultimate causal focus shifted on the one hand to the Platonic regular polyhedra within which Kepler held they were embedded and which thus ultimately defined the dimensions and eccentricities of planetary orbits, and on the other hand to the rotating sun as the central inner driver of planetary motion, itself rotated by its own motor soul.However, an immobile stellar sphere was a lasting remnant of physical celestial spheres in Kepler's cosmology.

But hard physical spheres still featured in both Galileo's and Newton's early celestial mechanics. Galileo initially considered the planets to be rolling around the upper surfaces of fixed perfectly smooth spheres driven by their own impetus and gravity. Thus for a long time Galileo fiercely resisted the Tychonic theory that comets are superlunary because it destroyed his initial spherist celestial mechanics by knocking away the necessary counter-gravitational supporting surfaces of the rolling planets. For he was unable to explain circular orbits as closed curve projectiles driven by a centrifugal impetus and centripetal gravity. And Newton calculated the centrifugal pressure that would be exerted by the Moon on the lower concave surface of the lunar orb in his 1660s analysis of lunar gravity.

Literary and symbolic expressions

Dante and Beatrice gaze upon the highest Heaven; from Gustave Doré's illustrations to the Divine Comedy, Paradiso Canto 28, lines 16–39.

In Cicero's Dream of Scipio, the elder Scipio Africanus describes an ascent through the celestial spheres, compared to which the Earth and the Roman Empire dwindle into insignificance. A commentary on the Dream of Scipio by the late Roman writer Macrobius (flourished c. 430 C.E.), which included a discussion of the various schools of thought on the order of the spheres, did much to spread the idea of the celestial spheres through the Early Middle Ages.

Nicole Oresme, Le livre du Ciel et du Monde, Paris, BnF, Manuscrits, Fr. 565, f. 69, (1377).

Some late medieval figures inverted the model of the celestial spheres to place God at the center and the Earth at the periphery. Near the beginning of the fourteenth century Dante, in the Paradiso of his Divine Comedy, described God as "a light at the center of the cosmos." Here the poet ascends beyond physical existence to the Empyrean Heaven, where he comes face to face with God himself and is granted understanding of both divine and human nature.

Later in the century, the illuminator of Nicole Oresme's Le livre du Ciel et du Monde, a translation of and commentary on Aristotle's De caelo produced for Oresme's patron, King Charles V, employed the same motif. He drew the spheres in the conventional order, with the Moon closest to the Earth and the stars highest, but the spheres were concave upwards, centered on God, rather than concave downwards, centered on the Earth. Below this figure Oresme quotes the Psalms that "The heavens declare the Glory of God and the firmament showeth his handiwork."

See also

• Equinox
• Solstice
• Zodiac

References

ISBN links support NWE through referral fees

• Aquinas, Thomas, and Richard J. Blackwell. 1963. Commentary on Aristotle's Physics. (New Haven, CT: Yale University Press. Bk4.L12. 534-536.
• Ariew, Roger. 1985. Medieval Cosmology. Chicago, IL: University of Chicago Press. ISBN 9780226169224.
• Aristotle, and Richard McKeon, ed. 2001. "Metaphysics," in The Basic Works of Aristotle. New York, NY: The Modern Library. ISBN 9780375757990.
• Clagett, Marshall. 1959. Science of Mechanics in the Middle Ages. Madison, WI: University of Wisconsin Press.
• Cohen, I.B., and A. Whitman. 1999. Principia. Berkeley, CA: University of California Press. ISBN 9780520088177.
• Cohen, I.B., and George E. Smith. 2002. The Cambridge Companion to Newton. Cambridge, UK: Cambridge Univ. Press. ISBN 9780521656962.
• Copernicus, Nicolaus. 1952. "On the Revolutions of the Heavenly Spheres," in Robert Maynard Hutchins, ed., and Encyclopedia Britannica Inc. 1952. Great Books of the Western World : 16 Ptolemy Copernicus Kepler. Chicago, IL: W. Benton.
• Dreyer, J.L.E. (1953). A history of astronomy from Thales to Kepler. New York, NY: Dover. ISBN 0486600793.
• Duhem, Pierre. 1911 ed. History of Physics. The Catholic Encyclopedia. Vol. 12. New York, NY: Robert Appleton Company. Retrieved February 8, 2009.
• Duhem, Pierre. 1959. Le Système du Monde: Histoire des doctrines cosmologiques de Platon à Copernic, 10 vols. Paris, FR: Hermann.
• Eastwood, Bruce. 1997. Astronomy in Christian Latin Europe c. 500 – c. 1150. Journal for the History of Astronomy. 28:235–258.
• Eastwood, Bruce, and Gerd Graßhoff. 2004. Planetary Diagrams for Roman Astronomy in Medieval Europe, ca. 800-1500. vol. 94, pt. 3. Philadelphia, PA: Transactions of the American Philosophical Society. ISBN 0871699435.
• Field, J.V. 1988. Kepler's geometrical cosmology. Chicago, IL: Chicago University Press. ISBN 0226248232.
• Galilei, Galileo, and Stillman Drake, trans. 1974. "Opere" VIII, in Two new sciences, including centers of gravity & force of percussion. Madison, WI: University of Wisconsin Press. ISBN 9780299064044.
• Gingerich, Owen. 1993. The eye of heaven: Ptolemy, Copernicus, Kepler. New York, NY: American Institute of Physics. ISBN 9780883188637.
• Goldstein, Bernard R., 1971. Al-Bitrūjī: On the Principles of Astronomy. vol. 1. New Haven, CT: Yale Univ. Press.
• Golino, Carlo, ed. 1966. Galileo Reappraised. Berkeley, CA: University of California Press.
• Grant, Edward. 1987. Celestial Orbs in the Latin Middle Ages. Isis 78:153-173; reprinted in Michael H. Shank, ed. 2000. The Scientific Enterprise in Antiquity and the Middle Ages. Chicago, IL: Univ. of Chicago Pr. ISBN 0226749517.
• __________. 1994. Planets, Stars, and Orbs: The Medieval Cosmos, 1200-1687. Cambridge, UK: Cambridge Univ. Pr. ISBN 052156509X.
• __________. 1996. The Foundations of Modern Science in the Middle Ages. Cambridge, UK; New York, NY: Cambridge University Press. ISBN 9780521567626.
• Jardine, Nicholas. 1982. The Significance of the Copernican Orbs. Journal for the History of Astronomy 13:168-194.
• Jarrell, R.A. 1989. "The contemporaries of Tycho Brahe," in Taton, and Wilson. 1989.
• Kepler, Johannes. "Epitome of Copernican Astronomy (Bks 4 & 5)," in Robert Maynard Hutchins, ed., and Encyclopedia Britannica Inc. 1952. Great Books of the Western World: 16 Ptolemy Copernicus Kepler. Chicago, IL: W. Benton.
• Koyré, Alexandre, and Mepham, trans. 1977. Galileo Studies. Hassocks, UK: Harvester Press. ISBN 0855273542.
• Langerman, Y. Tzvi. 1990. Ibn al Haytham's On the Configuration of the World. New York, NY: Garland Publishing. ISBN 9780824000417.
• Lewis, C.S. 1964. The Discarded Image: An Introduction to Medieval and Renaissance Literature. Cambridge, UK: Cambridge University Press.
• Lindberg, David C. ed. 1978. Science in the Middle Ages. Chicago, IL: University of Chicago Press. ISBN 9780226482323.
• Mach, Ernst. 1960. The Science of Mechanics. Lasalle, IL: Open Court. ISBN 9780875482026.
• Macrobius, and William Harris Stahl, trans. 1952. Commentary on the Dream of Scipio. New York, NY: Columbia Univ. Press.
• McCluskey, Stephen C. 1998. Astronomies and Cultures in Early Medieval Europe. Cambridge, UK: Cambridge Univ. Pr. ISBN 0521778522.
• Newton, Isaac, A. Rupert Hall, and Marie Boas Hall. 1962. Unpublished Scientific Papers of Isaac Newton. Cambridge, UK: Cambridge University Press.
• Oresme, Nicole, A.D. Menut, and A.J. Denomy trans. 1968. Le livre du ciel et du monde. Madison, WI: Univ. of Wisconsin Press.
• Rosen, Edward. 1985. The Dissolution of the Solid Celestial Spheres. Journal of the History of Ideas. 46(1):13-31.
• __________. (1939) 1959. Three Copernican Treatises. New York, NY: Dover.
• Sambursky, S. 1962. The Physical World of Late Antiquity. London, UK: Routledge & Kegan Paul. ISBN 9780710213051.
• Sargent, Steven, ed. 1982. On the threshold of exact science: Selected writings of Annaliese Maier on Late Medieval Natural Philosophy. Philadelphia, PA: University of Pennsylvania Press. ISBN 9780812278316.
• Schofield, C. 1989. "The Tychonic and Semi-Tychonic World Systems," in Taton, and Wilson. 1989.
• Sorabji, Richard. 1988. Matter, Space and Motion. Ithaca, NY: Cornell University Press. ISBN 9780801421945.
• __________. ed. 1987. Philoponus and the Rejection of Aristotelian Science. Ithaca, NY: Cornell Univ. Pr. ISBN 9780801420498.
• __________. 2004. The Philosophy of the Commentators, 200-600 C.E.: Volume 2 Physics. London, UK: Duckworth. ISBN 9780715632468.
• Taton, R., and C. Wilson, eds. 1989. The General History of Astronomy: Volume 2 Planetary astronomy from the Renaissance to the rise of astrophysics Part A Tycho Brahe to Newton. Cambridge, UK: Cambridge University Press. ISBN 9780521242547.
• Thoren, Victor E. 1979. The Comet of 1577 and Tycho Brahe's System of the World. Archives Internationales d'Histoire des Sciences. 29:53-67.
• Thoren, Victor E. 1989. Tycho Brahe in Taton, and Wilson. 1989.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Celestial_sphere  ^history
• Celestial_spheres  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Celestial sphere"

Note: Some restrictions may apply to use of individual images which are separately licensed.