Buffer solution
- Acid-base extraction
- Acid-base reaction
- Acid dissociation constant
- Acidity function
- Buffer solutions
- pH
- Proton affinity
- Self-ionization of water
- Acids:
- Lewis acids
- Mineral acids
- Organic acids
- Strong acids
- Superacids
- Weak acids
- Bases:
- Lewis bases
- Organic bases
- Strong bases
- Superbases
- Non-nucleophilic bases
- Weak bases
Buffer solutions are solutions that resist changes in pH (by resisting changes in hydronium ion and hydroxide ion concentrations) upon addition of small amounts of acid or base, or upon dilution. They usually consist of a weak acid and its conjugate base, or, less commonly, a weak base and its conjugate acid.
Buffer solutions are used in industry for chemical manufacturing and fermentation processes, and to set the proper conditions for dyeing fabrics. In research laboratories, buffers are used for chemical analyses, syntheses, and calibration of pH meters. In living organisms, these solutions maintain the correct pH for many enzymes to work. Blood plasma contains a buffer (of carbonic acid and bicarbonate) to maintain a pH of approximately 7.4.
The main component of a buffer solution, such as a weak acid or weak base, may be used as a buffering agent. The function of a buffering agent is to drive an acidic or alkaline solution to a certain pH and maintain it at that pH. As pH managers, they are important in many applications, including agriculture, food processing, medicine, and photography.
This article discusses buffer solutions prepared with water, but not other solvents. Also, these solutions are presented in terms of the Brønsted-Lowry notion of acids and bases, not the Lewis acid-base theory.
How buffers work
The ability of a buffer solution to resist changes in pH is the result of the equilibrium between a weak acid (HA) and its conjugate base (A−):
- HA(aq) + H2O(l) → H3O+(aq) + A−(aq)
Any alkali added to the solution is consumed by the hydronium ions. These ions are mostly regenerated as the equilibrium moves to the right and some of the acid dissociates into hydronium ions and the conjugate base. If a strong acid is added, the conjugate base is protonated, and the pH is almost entirely restored. This is an example of Le Chatelier's principle and the common ion effect.
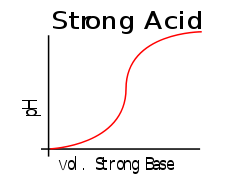
This contrasts with solutions of strong acids or strong bases, where any additional strong acid or base can greatly change the pH. This may be easier to see by comparing two graphs: When a strong acid is titrated with a strong base, the curve will have a large gradient throughout, showing that a small addition of base/acid will have a large effect; by comparison, a weak acid/strong base titration curve will have a smaller gradient when the pH is close to the pKa value.
When writing about buffer systems, they can be represented as the combination of a weak acid with the salt of its conjugate base, or the combination of a weak base with the salt of its conjugate acid.
Calculating pH values
The equilibrium reaction noted above has the following acid dissociation constant:
Simple manipulation with logarithms gives what is called the Henderson-Hasselbalch equation, which describe pH in terms of pKa:
In this equation,
- [A−] is the concentration of the conjugate base. It may be considered as coming completely from the salt, since the acid supplies relatively few anions compared to the salt.
- [HA] is the concentration of the acid. It may be considered as coming completely from the acid, since the salt supplies relatively few complete acid molecules (A − may extract H + from water to become HA) compared to the added acid.
Maximum buffering capacity is obtained when pH = pKa, and the buffer range is usually considered to be for pH = pKa ± 1.
Illustration of buffering effect: Sodium acetate/acetic acid
The acid dissociation constant for acetic acid-sodium acetate is given by the equation:
Since this equilibrium only involves a weak acid and base, it can be assumed that ionization of the acetic acid and hydrolysis of the acetate ions are negligible. In a buffer consisting of equal amounts of acetic acid and sodium acetate, the equilibrium equation simplifies to
- ,
and the pH of the buffer as is equal to the pKa.
To determine the effect of addition of a strong acid such as HCl, the following mathematics would provide the new pH. Since HCl is a strong acid, it is completely ionized in solution. This increases the concentration of H+ in solution, which then neutralizes the acetate by the following equation.
The consumed hydrogen ions change the effective number of moles of acetic acid and acetate ions:
After accounting for volume change to determine concentrations, the new pH could be calculated from the Henderson-Hasselbalch equation. Any neutralization will result in a small change in pH, since it is on a logarithmic scale..
Applications
Given their resistance to changes in pH, buffer solutions are very useful for chemical manufacturing and essential for many biochemical processes. The ideal buffer for a particular pH has a pKa equal to the pH desired, since a solution of this buffer would contain equal amounts of acid and base and be in the middle of the range of buffering capacity.
Buffer solutions are necessary to keep the correct pH for enzymes in many organisms to work. Many enzymes work only under very precise conditions; if the pH strays too far out of the margin, the enzymes slow or stop working and can denature, thus permanently disabling its catalytic activity. A buffer of carbonic acid (H2CO3) and bicarbonate (HCO3−) is present in blood plasma, to maintain a pH between 7.35 and 7.45.
Industrially, buffer solutions are used in fermentation processes and in setting the appropriate conditions for dyeing fabrics. They are also used in chemical analyses and syntheses, and for the calibration of pH meters.
Buffering agents
A buffering agent adjusts the pH of an acidic or alkaline solution and stabilizes it at that pH. Buffering agents have variable properties: some are acidic, others are basic; some are more soluble than others. They are useful for a variety of applications, including agriculture, food processing, medicine, and photography.
Buffering agents and buffer solutions are similar in that they both regulate the pH of a solution and resist changes in pH. They function based on the same chemical principles. They may, however, be distinguished by the following differences:
- A buffer solution maintains the pH of a system, preventing large changes in it, whereas a buffering agent modifies the pH of what it is placed into.
- A buffering agent is the active component of a buffer solution.
Examples
- Buffered aspirin has a buffering agent, such as magnesium oxide, that will maintain the pH of the aspirin as it passes through the patient’s stomach.
- Buffering agents are also present in antacid tablets, which are used mainly to lower acidity in the stomach.
- Monopotassium phosphate (MKP) is a buffering agent with a mildly acidic reaction. When used as a fertilizer component with urea or diammonium phosphate, it minimizes pH fluctuations that can cause loss of nitrogen.
Common buffer compounds used in biology
| Common Name | pKa at 25°C |
Buffer Range | Temp Effect (pH / °C)** |
Mol. Weight |
Full Compound Name |
|---|---|---|---|---|---|
| TAPS | 8.43 | 7.7 – 9.1 | −0.018 | 243.3 | 3-{[tris(hydroxymethyl)methyl]amino}propanesulfonic acid |
| Bicine | 8.35 | 7.6 – 9.0 | −0.018 | 163.2 | N,N-bis(2-hydroxyethyl)glycine |
| Tris | 8.06 | 7.5 – 9.0 | −0.028 | 121.14 | tris(hydroxymethyl)methylamine |
| Tricine | 8.05 | 7.4 – 8.8 | −0.021 | 179.2 | N-tris(hydroxymethyl)methylglycine |
| HEPES | 7.48 | 6.8 – 8.2 | −0.014 | 238.3 | 4-2-hydroxyethyl-1-piperazineethanesulfonic acid |
| TES | 7.40 | 6.8 – 8.2 | −0.020 | 229.20 | 2-{[tris(hydroxymethyl)methyl]amino}ethanesulfonic acid |
| MOPS | 7.20 | 6.5 – 7.9 | −0.015 | 209.3 | 3-(N-morpholino)propanesulfonic acid |
| PIPES | 6.76 | 6.1 – 7.5 | −0.008 | 302.4 | piperazine-N,N′-bis(2-ethanesulfonic acid) |
| Cacodylate | 6.27 | 5.0 – 7.4 | 138.0 | dimethylarsinic acid | |
| MES | 6.15 | 6.1 – 7.5 | −0.011 | 195.2 | 2-(N-morpholino)ethanesulfonic acid |
| Acetate | 4.76 | 3.8 – 5.8 | 59.04 | — |
** Values are approximate
Making buffer solutions
In general, preparing a buffer solution requires either:
- A weak acid and a salt of the acid's conjugate base.
- Or a weak base and a salt of the base's conjugate acid.
Both of which in sufficient amounts to maintain the ability to buffer
Example: Citric acid-phosphate buffer
Make up 0.1M citric acid and 0.2M Disodium hydrogen phosphate solutions then mix as follows to make a 100 ml solution:
| pH | 0.2M Na2HPO4 | 0.1M Citric Acid |
|---|---|---|
| 3.0 | 20.55 ml | 79.45 ml |
| 4.0 | 38.55 ml | 61.45 ml |
| 5.0 | 51.50 ml | 48.50 ml |
| 6.0 | 63.15 ml | 36.85 ml |
| 7.0 | 82.35 ml | 17.65 ml |
| 8.0 | 97.25 ml | 2.75 ml |
See also
ReferencesISBN links support NWE through referral fees
- Atkins, Peter, and Loretta Jones. 2008. Chemical Principles: The Quest for Insight. 4th ed. New York: W.H. Freeman. ISBN 0716799030
- Chang, Raymond. 2006. Chemistry. 9th ed. New York: McGraw-Hill Science/Engineering/Math. ISBN 0073221031
- Cotton, F. Albert, and Geoffrey Wilkinson. 1980. Advanced Inorganic Chemistry. 4th ed. New York: Wiley. ISBN 0471027758
- Harris, Daniel C. 2006. Quantitative Chemical Analysis. 7th ed. New York: W. H. Freeman. ISBN 978-0716776949
- McMurry, J., and R.C. Fay. 2004. Chemistry. 4th ed. Upper Saddle River, NJ: Prentice Hall. ISBN 0131402080
External links
All links retrieved November 22, 2023.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.

![{\displaystyle \mathrm {K_{a}={\frac {[H^{+}][A^{-}]}{[HA]}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/14a41818964da5798042c1d67a87ead832bce748)
![{\displaystyle pH=pK_{a}+log_{10}{\frac {[A^{-}]}{[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f6fb8355d64468056c75106ed979a6122d5b2b)
![{\displaystyle \mathrm {K_{a}={\frac {[H^{+}][CH_{3}COO^{-}]}{[CH_{3}COOH]}}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0241dab101bee7364ef4f8565e01e4a1cfa1d79)
![{\displaystyle \mathrm {K_{a}=[H^{+}]} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/203cc492d8e93bcc8e576b29dd52a365ecc976f1)


