Exponential function

The exponential function is one of the most important functions in mathematics. The application of this function to a value x is written as exp(x). Equivalently, this can be written in the form e^x, where e is a mathematical constant, the base of the natural logarithm, which equals approximately 2.718281828, and is also known as Euler's number.

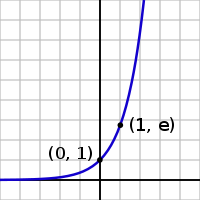
The exponential function is nearly flat (climbing slowly) for negative values of x, climbs quickly for positive values of x, and equals 1 when x is equal to 0. Its y value always equals the slope at that point.

As a function of the real variable x, the graph of y=a^x is always positive (above the x axis) and increasing (viewed left-to-right). It never touches the x axis, although it gets arbitrarily close to it (thus, the x axis is a horizontal asymptote to the graph). Its inverse function, the logarithm, $\log _{a}(x)=y\,$, is defined for all positive x.

Sometimes, especially in the sciences, the term exponential function is more generally used for functions of the form ka^x, where a, called the base, is any positive real number not equal to one.

In general, the variable x can be any real or complex number, or even an entirely different kind of mathematical object.

Some of the applications of the exponential function include modeling decay and/or growth in populations, economics, fatigue of materials, and amounts of radioactive material.

Properties

Most simply, exponential functions multiply at a constant rate. For example the population of a bacterial culture which doubles every 20 minutes can (approximatively, as this is not really a continuous problem) be expressed as an exponential, as can the value of a car which decreases by 10% per year.

Exponential functions "translate between addition and multiplication" as is expressed in the first three and the fifth of the following exponential laws:

$\,\!\,a^{0}=1$

$\,\!\,a^{1}=a$

$\,\!\,a^{x+y}=a^{x}a^{y}$

$\,\!\,a^{xy}=\left(a^{x}\right)^{y}$

$\,\!\,{1 \over a^{x}}=\left({1 \over a}\right)^{x}=a^{-x}$

$\,\!\,a^{x}b^{x}=(ab)^{x}$

These are valid for all positive real numbers a and b and all real numbers x and y. Expressions involving fractions and roots can often be simplified using exponential notation:

$\,{1 \over a}=a^{-1}$

and, for any a > 0, real number b, and integer n > 1:

$\,{\sqrt[{n}]{a^{b}}}=\left({\sqrt[{n}]{a}}\right)^{b}=a^{b/n}.$

Derivatives and differential equations

The importance of exponential functions in mathematics and the sciences stems mainly from properties of their derivatives. In particular,

$\,{d \over dx}e^{x}=e^{x}$

That is, e^x is its own derivative. Functions of the form $\,Ke^{x}$ for constant K are the only functions with that property. (This follows from the Picard-Lindelöf theorem, with $\,y(t)=e^{t},y(0)=K$ and $\,f(t,y(t))=y(t)$.) Other ways of saying the same thing include:

• The slope of the graph at any point is the height of the function at that point.
• The rate of increase of the function at x is equal to the value of the function at x.
• The function solves the differential equation $\,y'=y$.
• exp is a fixed point of derivative as a functional

In fact, many differential equations give rise to exponential functions, including the Schrödinger equation and the Laplace's equation as well as the equations for simple harmonic motion.

For exponential functions with other bases:

$\,{d \over dx}a^{x}=(\ln a)a^{x}$

Thus any exponential function is a constant multiple of its own derivative.

If a variable's growth or decay rate is proportional to its size — as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay — then the variable can be written as a constant times an exponential function of time.

Furthermore for any differentiable function f(x), we find, by the chain rule:

$\,{d \over dx}e^{f(x)}=f'(x)e^{f(x)}$.

Double exponential function

The term double exponential function can have two meanings:

• a function with two exponential terms, with different exponents
• a function $\,f(x)=a^{a^{x}}$; this grows even faster than an exponential function; for example, if a = 10: f(−1) = 1.26, f(0) = 10, f(1) = 10¹⁰, f(2) = 10¹⁰⁰ = googol, ..., f(100) = googolplex.

Factorials grow faster than exponential functions, but slower than double-exponential functions. Fermat numbers, generated by $\,F(m)=2^{2^{m}}+1$ and double Mersenne numbers generated by $\,MM(p)=2^{(2^{p}-1)}-1$ are examples of double exponential functions.

See also

• e (mathematical constant)
• Characterizations of the exponential function
• Exponential growth
• Exponentiation
• List of integrals of exponential functions
• List of exponential topics

References

ISBN links support NWE through referral fees

• Konyagin, Sergei and Igor Shparlinski. 1999. Character Sums with Exponential Functions and their Applications. Cambridge, UK: Cambridge University Press. ISBN 0521642639.
• Fried, H.M. 2002. Green's Functions and Ordered Exponentials. Cambridge, UK: Cambridge University Press. ISBN 0521443903.
• Carico, Charles C. 1974. Exponential and logarithmic functions (Wadsworth precalculus mathematics series). Belmont, CA: Wadsworth Pub. Co. ISBN 0534003141.

External links

• Complex exponential function. Retrieved September 9, 2007.
• Derivative of exponential function. Retrieved September 9, 2007.
• Weisstein, Eric W. Exponential Function. Retrieved September 9, 2007.
• Mathews, John H. Complex Exponential Function Module. Retrieved September 9, 2007.
• Taylor Series Expansions of Exponential Functions. efunda. Retrieved September 9, 2007.
• Complex exponential interactive graphic. Retrieved September 9, 2007.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Exponential function  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Exponential function"

Note: Some restrictions may apply to use of individual images which are separately licensed.