Exponential function

The exponential function is one of the most important functions in mathematics. The application of this function to a value x is written as exp(x). Equivalently, this can be written in the form e^x, where e is a mathematical constant, the base of the natural logarithm, which equals approximately 2.718281828, and is also known as Euler's number.

The exponential function is nearly flat (climbing slowly) for negative values of x, climbs quickly for positive values of x, and equals 1 when x is equal to 0. Its y value always equals the slope at that point.

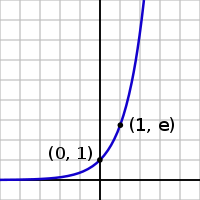
As a function of the real variable x, the graph of y=e^x is always positive (above the x axis) and increasing (viewed left-to-right). It never touches the x axis, although it gets arbitrarily close to it (thus, the x axis is a horizontal asymptote to the graph). Its inverse function, the natural logarithm, ln(x), is defined for all positive x.

Sometimes, especially in the sciences, the term exponential function is more generally used for functions of the form ka^x, where a, called the base, is any positive real number not equal to one. This article will focus initially on the exponential function with base e, Euler's number.

In general, the variable x can be any real or complex number, or even an entirely different kind of mathematical object; see the formal definition below.

Some of the applications of the exponential function include modeling decay and/or growth in populations, economics, fatigue of materials, and amounts of radioactive material.

Formal definition

File:Exp series.gif

The exponential function (in blue), and the sum of the first n+1 terms of the power series on the left (in red).

The exponential function e^x can be defined in a variety of equivalent ways, as an infinite series. In particular it may be defined by a power series:

$e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots$

or as the limit of a sequence:

$e^{x}=\lim _{n\to \infty }\left(1+{x \over n}\right)^{n}.$

In these definitions, n! stands for the factorial of n, and x can be any real number, complex number, element of a Banach algebra (for example, a square matrix), or member of the field of p-adic numbers.

For further explanation of these definitions and a proof of their equivalence, see the article Characterizations of the exponential function.

Properties

Most simply, exponential functions multiply at a constant rate. For example the population of a bacterial culture which doubles every 20 minutes can (approximatively, as this is not really a continuous problem) be expressed as an exponential, as can the value of a car which decreases by 10% per year.

Using the natural logarithm, one can define more general exponential functions. The function

$\,\!\,a^{x}=(e^{\ln a})^{x}=e^{x\ln a}$

defined for all a > 0, and all real numbers x, is called the exponential function with base a. Note that this definition of $\,a^{x}$ rests on the previously established existence of the function $\,e^{x}$, defined for all real numbers. (Here, we neither formally nor conceptually clarify whether such a function exists or what non-natural exponents are supposed to mean.)

Note that the equation above holds for a = e, since

$\,\!\,e^{x\ln e}=e^{x\cdot 1}=e^{x}.$

Exponential functions "translate between addition and multiplication" as is expressed in the first three and the fifth of the following exponential laws:

$\,\!\,a^{0}=1$

$\,\!\,a^{1}=a$

$\,\!\,a^{x+y}=a^{x}a^{y}$

$\,\!\,a^{xy}=\left(a^{x}\right)^{y}$

$\,\!\,{1 \over a^{x}}=\left({1 \over a}\right)^{x}=a^{-x}$

$\,\!\,a^{x}b^{x}=(ab)^{x}$

These are valid for all positive real numbers a and b and all real numbers x and y. Expressions involving fractions and roots can often be simplified using exponential notation:

$\,{1 \over a}=a^{-1}$

and, for any a > 0, real number b, and integer n > 1:

$\,{\sqrt[{n}]{a^{b}}}=\left({\sqrt[{n}]{a}}\right)^{b}=a^{b/n}.$

Derivatives and differential equations

The importance of exponential functions in mathematics and the sciences stems mainly from properties of their derivatives. In particular,

$\,{d \over dx}e^{x}=e^{x}$

That is, e^x is its own derivative. Functions of the form $\,Ke^{x}$ for constant K are the only functions with that property. (This follows from the Picard-Lindelöf theorem, with $\,y(t)=e^{t},y(0)=K$ and $\,f(t,y(t))=y(t)$.) Other ways of saying the same thing include:

• The slope of the graph at any point is the height of the function at that point.
• The rate of increase of the function at x is equal to the value of the function at x.
• The function solves the differential equation $\,y'=y$.
• exp is a fixed point of derivative as a functional

In fact, many differential equations give rise to exponential functions, including the Schrödinger equation and the Laplace's equation as well as the equations for simple harmonic motion.

For exponential functions with other bases:

$\,{d \over dx}a^{x}=(\ln a)a^{x}$

Thus any exponential function is a constant multiple of its own derivative.

If a variable's growth or decay rate is proportional to its size — as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay — then the variable can be written as a constant times an exponential function of time.

Furthermore for any differentiable function f(x), we find, by the chain rule:

$\,{d \over dx}e^{f(x)}=f'(x)e^{f(x)}$.

Numerical value

To obtain the numerical value of the exponential function, the infinite series can be rewritten as :

$\,e^{x}={1 \over 0!}+x\,\left({1 \over 1!}+x\,\left({1 \over 2!}+x\,\left({1 \over 3!}+\cdots \right)\right)\right)$

$\,=1+{x \over 1}\left(1+{x \over 2}\left(1+{x \over 3}\left(1+\cdots \right)\right)\right)$

This expression will converge quickly if we can ensure that x is less than one.

To ensure this, we can use the following identity.

$\,e^{x}\,$	$\,=e^{z+f}\,$
	$\,=e^{z}\times \left[{1 \over 0!}+f\,\left({1 \over 1!}+f\,\left({1 \over 2!}+f\,\left({1 \over 3!}+\cdots \right)\right)\right)\right]$

• Where $\,z$ is the integer part of $\,x$
• Where $\,f$ is the fractional part of $\,x$
• Hence, $\,f$ is always less than 1 and $\,f$ and $\,z$ add up to $\,x$.

The value of the constant e^z can be calculated beforehand by multiplying e with itself z times.

Computing exp(x) for real x

An even better algorithm can be found as follows.

First, notice that the answer y = e^x is usually a floating point number represented by a mantissa m and an exponent n so y = m 2ⁿ for some integer n and suitably small m. Thus, we get:

$\,y=m\,2^{n}=e^{x}.$

Taking log on both sides of the last two gives us:

$\,\ln(y)=\ln(m)+n\ln(2)=x.$

Thus, we get n as the result of dividing x by log(2) and finding the greatest integer that is not greater than this - that is, the floor function:

$\,n=\left\lfloor {\frac {x}{\ln(2)}}\right\rfloor .$

Having found n we can then find the fractional part u like this:

$\,u=x-n\ln(2).$

The number u is small and in the range 0 ≤ u < ln(2) and so we can use the previously mentioned series to compute m:

$\,m=e^{u}=1+u(1+u({\frac {1}{2!}}+u({\frac {1}{3!}}+u(....)))).$

Having found m and n we can then produce y by simply combining those two into a floating point number:

$\,y=e^{x}=m\,2^{n}.$

On the complex plane

File:Complex exp.jpg

Exponential function on the complex plane. The transition from dark to light colors shows that the magnitude of the exponential function is increasing to the right. The periodic horizontal bands indicate that the exponential function is periodic in the imaginary part of its argument.

When considered as a function defined on the complex plane, the exponential function retains the important properties

$\,\!\,e^{z+w}=e^{z}e^{w}$

$\,\!\,e^{0}=1$

$\,\!\,e^{z}\neq 0$

$\,\!\,{d \over dz}e^{z}=e^{z}$

for all z and w.

It is a holomorphic function which is periodic with imaginary period $\,2\pi i$ and can be written as

$\,\!\,e^{a+bi}=e^{a}(\cos b+i\sin b)$

where a and b are real values. This formula connects the exponential function with the trigonometric functions and to the hyperbolic functions. Thus we see that all elementary functions except for the polynomials spring from the exponential function in one way or another.

See also Euler's formula.

Extending the natural logarithm to complex arguments yields a multi-valued function, ln(z). We can then define a more general exponentiation:

$\,\!\,z^{w}=e^{w\ln z}$

for all complex numbers z and w. This is also a multi-valued function. The above stated exponential laws remain true if interpreted properly as statements about multi-valued functions.

The exponential function maps any line in the complex plane to a logarithmic spiral in the complex plane with the center at the origin. Two special cases might be noted: when the original line is parallel to the real axis, the resulting sprial never closes in on itself; when the original line is parallel to the imaginary axis, the resulting spiral is a circle of some radius.

• Plots of the exponential function on the complex plane
• ExponentialRe.png

  z = Re(e^x+iy)

• ExponentialIm.png

  z = Im(e^x+iy)

• ExponentialAbs.png
• ExponentialAll.png

Computation of exp(z) for a complex z

This is fairly straightforward given the formula

$\,e^{x+yi}=e^{x}e^{yi}=e^{x}(\cos(y)+i\sin(y))=e^{x}\cos(y)+ie^{x}\sin(y).$

Note that the argument y to the trigonometric functions are real.

Computation of $\,a^{b}$ where both a and b are complex

This is also straightforward given the formulae:

if a = x + yi and b = u + vi we can first convert a to polar co-ordinates by finding a $\,\theta$ and an $\,r$ such that:

$\,re^{{\theta }i}=r\cos \theta +ir\sin \theta =a=x+yi$

or

$\,x=r\cos \theta$ and $\,y=r\sin \theta .$

Thus, $\,x^{2}+y^{2}=r^{2}$ or $\,r={\sqrt {x^{2}+y^{2}}}$ and $\,\tan \theta ={\frac {y}{x}}$ or $\,\theta =\operatorname {atan2} (y,x).$

Now, we have that:

$\,a=re^{{\theta }i}=e^{\log(r)+{\theta }i}$

so:

$\,a^{b}=(e^{\log(r)+{\theta }i})^{u+vi}=e^{(\log(r)+{\theta }i)(u+vi)}$

The exponent is thus a simple multiplication of two complex values yielding a complex result which can then be brought back to regular cartesian format by the formula:

$\,e^{p+qi}=e^{p}(\cos(q)+i\sin(q))=e^{p}\cos(q)+ie^{p}\sin(q)$

where p is the real part of the multiplication:

$\,p=u\log(r)-v\theta$

and q is the imaginary part of the multiplication:

$\,q=v\log(r)+u\theta .$

Note that all of $\,x,y,u,v,r,$ $\,\theta$, $\,p$ and $\,q$ are all real values in these computations. The result of $\,a^{b}$ is thus $\,p+qi$.

Also note that since we compute and use $\,\log(r)$ rather than r itself you don't have to compute the square root. Instead simply compute $\,\log(r)={\frac {1}{2}}\log(x^{2}+y^{2})$. Watch out for potential overflow though and possibly scale down the x and y prior to computing $\,x^{2}+y^{2}$ by a suitable power of 2 if $\,x$ and $\,y$ are so large that you would overflow. If you instead run the risk of underflow, scale up by a suitable power of 2 prior to computing the sum of the squares. In either case you then get the scaled version of $\,x$ - we can call it $\,x'$ and the scaled version of $\,y$ - call it $\,y'$ and so you get:

$\,x=x'2^{s}$ and $\,y=y'2^{s}$

where $\,2^{s}$ is the scaling factor.

Then you get $\,\log(r)={\frac {1}{2}}(\log(x'^{2}+y'^{2})+s)$ where $\,x'$ and $\,y'$ are scaled so that the sum of the squares will not overflow or underflow. If $\,x$ is very large while $\,y$ is very small so that you cannot find such a scaling factor you will overflow anyway and so the sum is essentially equal to $\,x^{2}$ since y is ignored and thus you get $\,r=|x|$ in this case and $\,\log(r)=\log(|x|)$. The same happens in the case when $\,x$ is very small and $\,y$ is very large. If both are very large or both are very small you can find a scaling factor as mentioned earlier.

Note that this function is, in general, multivalued for complex arguments. This is because rotation of a single point through any angle plus 360 degrees, or $2\pi$ radians, is the same as rotation through the angle itself. So $\theta$ above is not unique: $\theta _{k}=\theta +2\pi k$ for any integer $k$ would do as well. The convention though is that when $a^{b}$ is taken as a single value it must be that for $k=0$, ie. we use the smallest possible (in magnitude) value of theta, which has a magnitude of, at most, $\pi$.

Matrices and Banach algebras

The definition of the exponential function given above can be used verbatim for every Banach algebra, and in particular for square matrices (in which case the function is called the matrix exponential). In this case we have

$\,\ e^{x+y}=e^{x}e^{y}{\mbox{ if }}xy=yx$

$\,\ e^{0}=1$

$\,\ e^{x}$ is invertible with inverse $\,\ e^{-x}$

the derivative of $\,\ e^{x}$ at the point $\,\ x$ is that linear map which sends $\,\ u$ to $\,\ ue^{x}$.

In the context of non-commutative Banach algebras, such as algebras of matrices or operators on Banach or Hilbert spaces, the exponential function is often considered as a function of a real argument:

$\,\ f(t)=e^{tA}$

where A is a fixed element of the algebra and t is any real number. This function has the important properties

$\,\ f(s+t)=f(s)f(t)$

$\,\ f(0)=1$

$\,\ f'(t)=Af(t)$

Double exponential function

The term double exponential function can have two meanings:

• a function with two exponential terms, with different exponents
• a function $\,f(x)=a^{a^{x}}$; this grows even faster than an exponential function; for example, if a = 10: f(−1) = 1.26, f(0) = 10, f(1) = 10¹⁰, f(2) = 10¹⁰⁰ = googol, ..., f(100) = googolplex.

Factorials grow faster than exponential functions, but slower than double-exponential functions. Fermat numbers, generated by $\,F(m)=2^{2^{m}}+1$ and double Mersenne numbers generated by $\,MM(p)=2^{(2^{p}-1)}-1$ are examples of double exponential functions.

See also

• e (mathematical constant)
• Characterizations of the exponential function
• Exponential growth
• Exponentiation
• List of integrals of exponential functions
• List of exponential topics

References

ISBN links support NWE through referral fees

• Konyagin, Sergei and Igor Shparlinski. 1999. Character Sums with Exponential Functions and their Applications. Cambridge, UK: Cambridge University Press. ISBN 0521642639.
• Fried, H.M. 2002. Green's Functions and Ordered Exponentials. Cambridge, UK: Cambridge University Press. ISBN 0521443903.
• Carico, Charles C. 1974. Exponential and logarithmic functions (Wadsworth precalculus mathematics series). Belmont, CA: Wadsworth Pub. Co. ISBN 0534003141.

External links

• Complex exponential function. Retrieved September 9, 2007.
• Derivative of exponential function. Retrieved September 9, 2007.
• Weisstein, Eric W. Exponential Function. Retrieved September 9, 2007.
• Mathews, John H. Complex Exponential Function Module. Retrieved September 9, 2007.
• Taylor Series Expansions of Exponential Functions. efunda. Retrieved September 9, 2007.
• Complex exponential interactive graphic. Retrieved September 9, 2007.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Exponential function  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Exponential function"

Note: Some restrictions may apply to use of individual images which are separately licensed.