|
|
| (20 intermediate revisions by 7 users not shown) |
| Line 1: |
Line 1: |
| − | {{Claimed}} | + | {{Images OK}}{{Submitted}}{{Approved}}{{Paid}}{{Copyedited}} |
| − | The '''exponential function''' is one of the most important [[function (mathematics)|function]]s in [[mathematics]]. The application of this function to a value '''''x''''' is written as '''exp(''x'')'''. Equivalently, this can be written in the form '''''e<sup>x</sup>''''', where '''''e''''' is a mathematical constant, the [[e (mathematical constant)|base of the natural logarithm]], which equals approximately 2.718281828, and is also known as [[Euler]]'s number.
| + | [[image:exp.svg|thumb|200px|right|Graph of ''y'' = ''e''<sup>''x''</sup>. The exponential function is nearly flat (climbing slowly) for negative values of ''x'', climbs quickly for positive values of ''x'', and equals 1 when ''x'' is equal to 0. Its ''y'' value always equals the [[slope]] at that point.]] |
| | | | |
| − | [[image:exp.svg|thumb|200px|right|The exponential function is nearly flat (climbing slowly) for negative values of ''x'', climbs quickly for positive values of ''x'', and equals 1 when ''x'' is equal to 0. Its ''y'' value always equals the [[slope]] at that point.]]
| + | The '''exponential function''' is one of the most important [[function (mathematics)|function]]s in [[mathematics]]. For a variable '''''x''''', this function is written as '''exp(''x'')''' or '''''e<sup>x</sup>''''', where '''''e''''' is a mathematical constant, the [[e (mathematical constant)|base of the natural logarithm]], which equals approximately 2.718281828, and is also known as [[Euler]]'s number. Here, ''e'' is called the '''base''' and ''x'' is called the '''exponent'''. In a more general form, an exponential function can be written as '''''a<sup>x</sup>''''', where ''a'' is a constant and ''x'' is a variable. |
| | | | |
| − | As a function of the ''[[real number|real]]'' variable ''x'', the [[graph of a function|graph]] of ''y''=''e''<sup>''x''</sup> is always positive (above the ''x'' axis) and increasing (viewed left-to-right). It never touches the ''x'' axis, although it gets arbitrarily close to it (thus, the ''x'' axis is a horizontal [[asymptote]] to the graph). Its [[inverse function]], the [[natural logarithm]], ln''(x)'', is defined for all positive ''x''.
| + | The graph of ''y'' = ''e''<sup>''x''</sup> is shown on the right. The graph is always positive (above the ''x'' axis) and increases from left to right. It never touches the ''x'' axis, although it gets extremely close to it. In other words, the ''x'' axis is a horizontal [[asymptote]] to the graph. Its [[inverse function]], the [[logarithm]], <math> \log_e(x) = y \,</math>, is defined for all positive ''x''. |
| | | | |
| − | Sometimes, especially in the [[science]]s, the term '''exponential function''' is more generally used for functions of the form ''ka''<sup>''x''</sup>, where ''a'', called the ''base'', is any positive real number not equal to one. This article will focus initially on the exponential function with base ''e'', Euler's number. | + | Sometimes, especially in the [[science]]s, the term '''exponential function''' is more generally used for functions of the form ''ka''<sup>''x''</sup>, where ''a'' is any positive real number not equal to one. |
| | | | |
| − | In general, the [[variable]] ''x'' can be any real or [[complex number]], or even an entirely different kind of mathematical object; see the [[#Formal definition|formal definition below]]. | + | In general, the [[variable]] ''x'' can be any real or [[complex number]], or even an entirely different kind of mathematical object. |
| | + | {{toc}} |
| | + | Some applications of the exponential function include modeling growth in populations, economic changes, fatigue of materials, and [[radioactive decay]]. |
| | | | |
| | ==Properties== | | ==Properties== |
| − | Most simply, exponential functions multiply at a constant rate. For example the population of a bacterial culture which doubles every 20 minutes can (approximatively, as this is not really a continuous problem) be expressed as an exponential, as can the value of a car which decreases by 10% per year. | + | |
| | + | Most simply, exponential functions multiply at a constant rate. For example the population of a bacterial culture that doubles every 20 minutes can be expressed (approximatively, as this is not really a continuous problem) as an exponential, as can the value of a car that decreases by 10 percent per year. |
| | | | |
| | Using the natural logarithm, one can define more general exponential functions. The function | | Using the natural logarithm, one can define more general exponential functions. The function |
| | : <math>\,\!\, a^x=(e^{\ln a})^x=e^{x \ln a}</math> | | : <math>\,\!\, a^x=(e^{\ln a})^x=e^{x \ln a}</math> |
| − | defined for all ''a'' > 0, and all real numbers ''x'', is called the '''exponential function with base''' '''''a'''''. Note that this definition of <math>\, a^x </math> rests on the previously established existence of the function <math>\, e^x </math>, defined for all real numbers. (Here, we neither formally nor conceptually clarify whether such a function exists or what non-natural exponents are supposed to mean.) | + | defined for all ''a'' > 0, and all real numbers ''x'', is called the '''exponential function with base''' '''''a'''''. Note that this definition of <math>\, a^x </math> rests on the previously established existence of the function <math>\, e^x </math>, defined for all real numbers. |
| − | | |
| − | Note that the equation above holds for ''a'' = ''e'', since
| |
| − | : <math>\,\!\, e^{x \ln e}=e^{x \cdot 1}=e^x.</math>
| |
| | | | |
| | Exponential functions "translate between addition and multiplication" as is expressed in the first three and the fifth of the following ''exponential laws'': | | Exponential functions "translate between addition and multiplication" as is expressed in the first three and the fifth of the following ''exponential laws'': |
| Line 32: |
Line 32: |
| | and, for any ''a'' > 0, real number ''b'', and integer ''n'' > 1: | | and, for any ''a'' > 0, real number ''b'', and integer ''n'' > 1: |
| | : <math>\,\sqrt[n]{a^b} = \left(\sqrt[n]{a}\right)^b = a^{b/n}.</math> | | : <math>\,\sqrt[n]{a^b} = \left(\sqrt[n]{a}\right)^b = a^{b/n}.</math> |
| | + | |
| | + | ==Formal definition== |
| | + | |
| | + | The exponential function e<sup>''x''</sup> can be defined in a variety of equivalent ways, as an [[infinite series]]. In particular, it may be defined by a [[power series]]: |
| | + | |
| | + | : <math>e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots</math> |
| | + | |
| | + | or as the [[limit of a sequence]]: |
| | + | |
| | + | : <math>e^x = \lim_{n \to \infty} \left( 1 + {x \over n} \right)^n.</math> |
| | + | |
| | + | In these definitions, ''n''! stands for the [[factorial]] of ''n'', and ''x'' can be any [[real number]], [[complex number]], element of a [[Banach algebra]] (for example, a [[square matrix]]), or member of the field of [[p-adic numbers|''p''-adic numbers]]. |
| | | | |
| | ==Derivatives and differential equations== | | ==Derivatives and differential equations== |
| | + | |
| | The importance of exponential functions in mathematics and the sciences stems mainly from properties of their [[derivative]]s. In particular, | | The importance of exponential functions in mathematics and the sciences stems mainly from properties of their [[derivative]]s. In particular, |
| | | | |
| Line 52: |
Line 65: |
| | Thus ''any'' exponential function is a [[constant]] multiple of its own derivative. | | Thus ''any'' exponential function is a [[constant]] multiple of its own derivative. |
| | | | |
| − | If a variable's growth or decay rate is [[proportionality (mathematics)|proportional]] to its size — as is the case in unlimited population growth (see [[Malthusian catastrophe]]), continuously compounded [[interest]], or [[radioactive decay]] — then the variable can be written as a constant times an exponential function of time. | + | If a variable's growth or decay rate is [[proportionality (mathematics)|proportional]] to its size—as is the case in unlimited population growth (see [[Malthusian catastrophe]]), continuously compounded [[interest]], or [[radioactive decay]]—then the variable can be written as a constant times an exponential function of time. |
| | | | |
| | Furthermore for any differentiable function ''f''(''x''), we find, by the [[chain rule]]: | | Furthermore for any differentiable function ''f''(''x''), we find, by the [[chain rule]]: |
| Line 58: |
Line 71: |
| | : <math>\,{d \over dx} e^{f(x)} = f'(x)e^{f(x)}</math>. | | : <math>\,{d \over dx} e^{f(x)} = f'(x)e^{f(x)}</math>. |
| | | | |
| − | ==Formal definition== | + | ==Double exponential function== |
| − | [[Image:Exp series.gif|right|thumb|The exponential function (in blue), and the sum of the first ''n''+1 terms of the power series on the left (in red).]]
| |
| − | | |
| − | The exponential function e<sup>''x''</sup> can be defined in a variety of equivalent ways, as an [[infinite series]]. In particular it may be defined by a [[power series]]:
| |
| − | | |
| − | : <math>e^x = \sum_{n = 0}^{\infty} {x^n \over n!} = 1 + x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots</math>
| |
| − | | |
| − | or as the [[limit of a sequence]]:
| |
| − | | |
| − | : <math>e^x = \lim_{n \to \infty} \left( 1 + {x \over n} \right)^n.</math>
| |
| − | | |
| − | In these definitions, ''n''! stands for the [[factorial]] of ''n'', and ''x'' can be any [[real number]], [[complex number]], element of a [[Banach algebra]] (for example, a [[square matrix]]), or member of the field of [[p-adic numbers|''p''-adic numbers]].
| |
| − | | |
| − | For further explanation of these definitions and a proof of their equivalence, see the article [[Characterizations of the exponential function]].
| |
| − | | |
| − | ==Numerical value==
| |
| − | To obtain the numerical value of the exponential function, the infinite series can be rewritten as :
| |
| − | | |
| − | :<math>\,e^x = {1 \over 0!} + x \, \left( {1 \over 1!} + x \, \left( {1 \over 2!} + x \, \left( {1 \over 3!} + \cdots \right)\right)\right)</math>
| |
| − | :<math>\,= 1 + {x \over 1} \left(1 + {x \over 2} \left(1 + {x \over 3} \left(1 + \cdots \right)\right)\right)</math>
| |
| − | | |
| − | This expression will converge quickly if we can ensure that x is less than one.
| |
| − | | |
| − | To ensure this, we can use the following identity.
| |
| − | | |
| − | :{|
| |
| − | |-
| |
| − | |<math>\,e^x\,</math>
| |
| − | |<math>\,=e^{z+f}\,</math>
| |
| − | |-
| |
| − | |
| |
| − | |<math>\,= e^z \times \left[{1 \over 0!} + f \, \left( {1 \over 1!} + f \, \left( {1 \over 2!} + f \, \left( {1 \over 3!} + \cdots \right)\right)\right)\right]</math>
| |
| − | |}
| |
| − | | |
| − | * Where <math>\,z</math> is the integer part of <math>\,x</math>
| |
| − | * Where <math>\,f</math> is the fractional part of <math>\,x</math>
| |
| − | * Hence, <math>\,f</math> is always less than 1 and <math>\,f</math> and <math>\,z</math> add up to <math>\,x</math>.
| |
| − | | |
| − | The value of the constant e<sup>z</sup> can be calculated beforehand by multiplying e with itself z times.
| |
| − | | |
| − | == Computing exp''(x)'' for real ''x'' ==
| |
| − | | |
| − | An even better algorithm can be found as follows.
| |
| − | | |
| − | First, notice that the answer ''y'' = ''e''<sup>''x''</sup> is usually a floating point number represented by a [[mantissa]] ''m'' and an exponent ''n'' so y = ''m'' 2<sup>''n''</sup> for some integer ''n'' and suitably small ''m''. Thus, we get:
| |
| − | | |
| − | :<math>\,y = m\,2^n = e^x.</math>
| |
| | | | |
| − | Taking log on both sides of the last two gives us:
| |
| − |
| |
| − | : <math>\,\ln(y) = \ln(m) + n\ln(2) = x.</math>
| |
| − |
| |
| − | Thus, we get ''n'' as the result of dividing ''x'' by log(2) and finding the greatest integer that is not greater than this - that is, the [[floor function]]:
| |
| − |
| |
| − | : <math>\,n = \left\lfloor\frac{x}{\ln(2)}\right\rfloor.</math>
| |
| − |
| |
| − | Having found ''n'' we can then find the fractional part ''u'' like this:
| |
| − |
| |
| − | : <math>\,u = x - n\ln(2).</math>
| |
| − |
| |
| − | The number ''u'' is small and in the range 0 ≤ ''u'' < ln(2) and so we can use the previously mentioned series to compute ''m'':
| |
| − |
| |
| − | :<math>\,m = e^u = 1 + u(1 + u(\frac{1}{2!} + u(\frac{1}{3!} + u(....)))).</math>
| |
| − |
| |
| − | Having found ''m'' and ''n'' we can then produce y by simply combining those two into a floating point number:
| |
| − |
| |
| − | : <math>\,y = e^x = m\,2^n.</math>
| |
| − |
| |
| − | == Continued fractions for ''e''<sup>''x''</sup> ==
| |
| − |
| |
| − | Via Euler's identity:
| |
| − |
| |
| − | :<math>\,
| |
| − | \ e^x=1+x+\frac{x^2}{2!}+\cdots=
| |
| − | 1+\cfrac{x}{1-\cfrac{x}{x+2-\cfrac{2x}{x+3-\cfrac{3x}{x+4-\cfrac{4x}{x+5-\cfrac{5x}{\ddots}}}}}}
| |
| − | </math>
| |
| − |
| |
| − | More advanced techniques are necessary to construct the following:
| |
| − |
| |
| − | :<math>\,
| |
| − | \ e^{2m/n}=1+\cfrac{2m}{(n-m)+\cfrac{m^2}{3n+\cfrac{m^2}{5n+\cfrac{m^2}{7n+\cfrac{m^2}{9n+\cfrac{m^2}{\ddots}}}}}}\,
| |
| − | </math>
| |
| − |
| |
| − | Setting m=x and n=2 yields
| |
| − |
| |
| − | :<math>\,
| |
| − | \ e^x=1+\cfrac{2x}{(2-x)+\cfrac{x^2}{6+\cfrac{x^2}{10+\cfrac{x^2}{14+\cfrac{x^2}{18+\cfrac{x^2}{\ddots}}}}}}\,
| |
| − | </math>
| |
| − |
| |
| − | == Computation of <math>\,a^n</math> for natural number (positive integer) ''n'' ==
| |
| − |
| |
| − | There is a fast way to compute <math>\,a^n</math> when ''n'' is a positive integer. It makes use of the fact that testing that such a number is odd is very easy on a computer and dividing by 2 is also fast by simply shifting all the bits to the right.
| |
| − |
| |
| − | step 1, initialize some variables<br/>
| |
| − | y := 1, k := n, f := a
| |
| − |
| |
| − | step 2, test k<br/>
| |
| − | '''if''' k is 0, '''go to''' step 7
| |
| − |
| |
| − | step 3, (k is not 0 here, test if k is even)<br/>
| |
| − | '''if''' k is even '''go to''' step 5
| |
| − |
| |
| − | step 4, (k is odd here, multiply in)<br/>
| |
| − | <math>\, y := y * f </math>
| |
| − |
| |
| − | step 5, (divide k by 2 / ignore remainder, divide by shift, also square f)<br/>
| |
| − | k := k '''shift right by''' 1
| |
| − | f := f * f
| |
| − |
| |
| − | step 6, (loop)<br/>
| |
| − | '''go back to''' step 2
| |
| − |
| |
| − | step 7, (done, y is result = a<sup>n</sup>)<br/>
| |
| − | '''return''' y
| |
| − |
| |
| − | In [[C (programming language)|C]] you can write the algorithm like this:
| |
| − |
| |
| − | <code>
| |
| − | double power(double a, unsigned int n)
| |
| − | {
| |
| − | double y = 1;
| |
| − | double f = a;
| |
| − | unsigned int k = n;
| |
| − | while (k != 0) {
| |
| − | if ((k & 1) != 0) y *= f;
| |
| − | k >>= 1;
| |
| − | f *= f;
| |
| − | }
| |
| − | return y;
| |
| − | }
| |
| − | </code>
| |
| − |
| |
| − | While a naive multiplication of a^100 would require 100 iterations of a loop multiplying a, this loop iterates only 7 times (The number 100 is written using 7 bits).
| |
| − |
| |
| − | This algorithm can easily be extended for signed integers by doing the following steps before and after:
| |
| − |
| |
| − | step 1. if k is negative, negate the value so we get a positive k. n still remembers the original value.
| |
| − |
| |
| − | step 2. Perform the above computation for <math>\,y = a^{|k|}</math>
| |
| − |
| |
| − | step 3. If n is negative, invert the result so y := 1/y. y is now the result of <math>\,a^n</math> for an integer n.
| |
| − |
| |
| − | == On the complex plane ==<!-- This section is linked from [[Complex plane]] —>
| |
| − | [[Image:Complex_exp.jpg|thumb|right|Exponential function on the complex plane. The transition from dark to light colors shows that the magnitude of the exponential function is increasing to the right. The periodic horizontal bands indicate that the exponential function is periodic in the imaginary part of its argument.]]
| |
| − |
| |
| − | When considered as a function defined on the [[complex number|complex plane]], the exponential function retains the important properties
| |
| − | : <math>\,\!\, e^{z + w} = e^z e^w</math>
| |
| − | : <math>\,\!\, e^0 = 1</math>
| |
| − | : <math>\,\!\, e^z \ne 0</math>
| |
| − | : <math>\,\!\, {d \over dz} e^z = e^z</math>
| |
| − | for all ''z'' and ''w''.
| |
| − |
| |
| − | It is a [[holomorphic function]] which is periodic with [[imaginary number|imaginary]] period <math>\,2 \pi i</math> and can be written as
| |
| − | : <math>\,\!\, e^{a + bi} = e^a (\cos b + i \sin b)</math>
| |
| − | where ''a'' and ''b'' are real values. This formula connects the exponential function with the [[trigonometric function]]s and to the [[hyperbolic function]]s. Thus we see that all [[elementary function (differential algebra)|elementary function]]s except for the [[polynomial]]s spring from the exponential function in one way or another.
| |
| − |
| |
| − | See also [[Euler's formula]].
| |
| − |
| |
| − | Extending the natural logarithm to complex arguments yields a [[multi-valued function]], ln''(z)''. We can then define a more general exponentiation:
| |
| − | : <math>\,\!\, z^w = e^{w \ln z}</math>
| |
| − | for all complex numbers ''z'' and ''w''. This is also a multi-valued function. The above stated exponential laws remain true if interpreted properly as statements about multi-valued functions.
| |
| − |
| |
| − | The exponential function maps any [[line (mathematics)|line]] in the complex plane to a [[logarithmic spiral]] in the complex plane with the center at the [[Origin (mathematics)|origin]]. Two special cases might be noted: when the original line is parallel to the real axis, the resulting sprial never closes in on itself; when the original line is parallel to the imaginary axis, the resulting spiral is a circle of some radius.
| |
| − |
| |
| − | <gallery caption="Plots of the exponential function on the complex plane">
| |
| − | Image:ExponentialRe.png| ''z'' = Re(e<sup>x+iy</sup>)
| |
| − | Image:ExponentialIm.png| ''z'' = Im(e<sup>x+iy</sup>)
| |
| − | Image:ExponentialAbs.png| ''z'' = |e<sup>x+iy</sup>|
| |
| − | Image:ExponentialAll.png
| |
| − | </gallery>
| |
| − |
| |
| − | == Computation of exp''(z)'' for a complex ''z'' ==
| |
| − |
| |
| − | This is fairly straightforward given the formula
| |
| − |
| |
| − | : <math>\,e^{x + yi} = e^xe^{yi} = e^x(\cos(y) + i \sin(y)) = e^x\cos(y) + ie^x\sin(y).</math>
| |
| − |
| |
| − | Note that the argument y to the trigonometric functions are real.
| |
| − |
| |
| − | == Computation of <math>\,a^b</math> where both ''a'' and ''b'' are complex ==
| |
| − |
| |
| − | This is also straightforward given the formulae:
| |
| − |
| |
| − | if a = x + yi and b = u + vi we can first convert a to polar co-ordinates by finding a <math>\,\theta</math> and an <math>\,r</math> such that:
| |
| − |
| |
| − | : <math>\,re^{{\theta}i} = r\cos\theta + i r\sin\theta = a = x + yi</math>
| |
| − |
| |
| − | or
| |
| − |
| |
| − | :<math>\, x = r\cos\theta</math> and <math>\,y = r\sin\theta.</math>
| |
| − |
| |
| − | Thus, <math>\,x^2 + y^2 = r^2</math> or <math>\,r = \sqrt{x^2 + y^2}</math> and
| |
| − | <math>\,\tan\theta = \frac{y}{x}</math> or <math>\,\theta = \operatorname{atan2}(y, x).</math>
| |
| − |
| |
| − | Now, we have that:
| |
| − |
| |
| − | : <math>\,a = re^{{\theta}i} = e^{\log(r) + {\theta}i}</math>
| |
| − |
| |
| − | so:
| |
| − |
| |
| − | : <math>\,a^b = (e^{\log(r) + {\theta}i})^{u + vi} = e^{(\log(r) + {\theta}i)(u + vi)}</math>
| |
| − |
| |
| − | The exponent is thus a simple multiplication of two complex values yielding a complex result which can then be brought back to regular cartesian format by the formula:
| |
| − |
| |
| − | : <math>\,e^{p + qi} = e^p(\cos(q) + i\sin(q)) = e^p\cos(q) + ie^p\sin(q)</math>
| |
| − |
| |
| − | where ''p'' is the real part of the multiplication:
| |
| − | : <math>\,p = u\log(r) - v\theta</math>
| |
| − |
| |
| − | and ''q'' is the imaginary part of the multiplication:
| |
| − | : <math>\,q = v\log(r) + u\theta.</math>
| |
| − |
| |
| − | Note that all of <math>\,x, y, u, v, r,</math> <math>\,\theta</math>, <math>\,p</math> and <math>\,q</math> are all real values in these computations. The result of <math>\,a^b</math> is thus <math>\,p + qi</math>.
| |
| − |
| |
| − | Also note that since we compute and use <math>\,\log(r)</math> rather than r itself you don't have to compute the square root. Instead simply compute <math>\,\log(r) = \frac12\log(x^2 + y^2)</math>. Watch out for potential overflow though and possibly scale down the x and y prior to computing <math>\,x^2 + y^2</math> by a suitable power of 2 if <math>\,x</math> and <math>\,y</math> are so large that you would overflow. If you instead run the risk of underflow, scale up by a suitable power of 2 prior to computing the sum of the squares. In either case you then get the scaled version of <math>\,x</math> - we can call it <math>\,x'</math> and the scaled version of <math>\,y</math> - call it <math>\,y'</math> and so you get:
| |
| − | :<math>\,x = x'2^s</math> and <math>\,y = y'2^s</math>
| |
| − |
| |
| − | where <math>\,2^s</math> is the scaling factor.
| |
| − |
| |
| − | Then you get <math>\,\log(r) = \frac12(\log(x'^2 + y'^2) + s)</math> where <math>\,x'</math> and <math>\,y'</math> are scaled so that the sum of the squares will not overflow or underflow. If <math>\,x</math> is very large while <math>\,y</math> is very small so that you cannot find such a scaling factor you will overflow anyway and so the sum is essentially equal to <math>\,x^2</math> since y is ignored and thus you get <math>\,r = |x|</math> in this case and <math>\,\log(r) = \log(|x|)</math>. The same happens in the case when <math>\,x</math> is very small and <math>\,y</math> is very large. If both are very large or both are very small you can find a scaling factor as mentioned earlier.
| |
| − |
| |
| − | Note that this function is, in general, [[multivalued function|multivalued]] for complex arguments. This is because rotation of a single point through any angle plus 360 degrees, or <math>2\pi</math> radians, is the same as rotation through the angle itself. So <math>\theta</math> above is not unique: <math>\theta_k = \theta + 2\pi k</math> for any integer <math>k</math> would do as well. The convention though is that when <math>a^b</math> is taken as a single value it must be that for <math>k = 0</math>, ie. we use the smallest possible (in magnitude) value of theta, which has a magnitude of, at most, <math>\pi</math>.
| |
| − |
| |
| − | == Matrices and Banach algebras ==
| |
| − | The definition of the exponential function given above can be used verbatim for every [[Banach algebra]], and in particular for square [[matrix (mathematics)|matrices]] (in which case the function is called the [[matrix exponential]]). In this case we have
| |
| − | : <math>\,\ e^{x + y} = e^x e^y \mbox{ if } xy = yx</math>
| |
| − | : <math>\,\ e^0 = 1</math>
| |
| − | : <math>\,\ e^x</math> is invertible with inverse <math>\,\ e^{-x}</math>
| |
| − | : the derivative of <math>\,\ e^x</math> at the point <math>\,\ x</math> is that linear map which sends <math>\,\ u</math> to <math>\,\ ue^x</math>.
| |
| − |
| |
| − | In the context of non-commutative Banach algebras, such as algebras of matrices or operators on [[Banach space|Banach]] or [[Hilbert space|Hilbert]] spaces, the exponential function is often considered as a function of a real argument:
| |
| − | : <math>\,\ f(t) = e^{t A}</math>
| |
| − | where ''A'' is a fixed element of the algebra and ''t'' is any real number. This function has the important properties
| |
| − | : <math>\,\ f(s + t) = f(s) f(t)</math>
| |
| − | : <math>\,\ f(0) = 1</math>
| |
| − | : <math>\,\ f'(t) = A f(t)</math>
| |
| − |
| |
| − | == On Lie algebras ==
| |
| − | The "exponential map" sending a [[Lie algebra]] to the [[Lie group]] that gave rise to it shares the above properties, which explains the terminology. In fact, since '''R''' is the Lie algebra of the Lie group of all positive real numbers with multiplication, the ordinary exponential function for real arguments is a special case of the Lie algebra situation. Similarly, since the Lie algebra M (''n'', '''R''') of all square real matrices belongs to the Lie group of all invertible square matrices, the exponential function for square matrices is a special case of the Lie algebra [[exponential map]].
| |
| − |
| |
| − | ==Double exponential function==
| |
| − | {{main|double exponential function}}
| |
| | The term '''''double exponential function''''' can have two meanings: | | The term '''''double exponential function''''' can have two meanings: |
| | *a function with two exponential terms, with different exponents | | *a function with two exponential terms, with different exponents |
| | *a function <math>\,f(x) = a^{a^x}</math>; this grows even faster than an exponential function; for example, if ''a'' = 10: ''f''(−1) = 1.26, ''f''(0) = 10, ''f''(1) = 10<sup>10</sup>, ''f''(2) = 10<sup>100</sup> = [[googol]], ..., ''f''(100) = [[googolplex]]. | | *a function <math>\,f(x) = a^{a^x}</math>; this grows even faster than an exponential function; for example, if ''a'' = 10: ''f''(−1) = 1.26, ''f''(0) = 10, ''f''(1) = 10<sup>10</sup>, ''f''(2) = 10<sup>100</sup> = [[googol]], ..., ''f''(100) = [[googolplex]]. |
| | | | |
| − | Factorials grow faster than exponential functions, but slower than double-exponential functions. [[Fermat number]]s, generated by <math>\,F(m) = 2^{2^m} + 1</math> and [[double Mersenne number]]s generated by <math>\,MM(p) = 2^{(2^p-1)}-1</math> are examples of double exponential functions.
| + | [[Factorial]]s grow faster than exponential functions, but slower than double-exponential functions. [[Fermat number]]s, generated by <math>\,F(m) = 2^{2^m} + 1</math> and [[double Mersenne number]]s generated by <math>\,MM(p) = 2^{(2^p-1)}-1</math> are examples of double exponential functions. |
| | | | |
| | ==See also== | | ==See also== |
| | | | |
| − | *[[e (mathematical constant)]] | + | * [[Logarithm]] |
| − | *[[Characterizations of the exponential function]] | + | * [[Radioactive decay]] |
| − | *[[Exponential growth]]
| |
| − | *[[Exponentiation]]
| |
| − | *[[List of integrals of exponential functions]]
| |
| − | *[[List of exponential topics]]
| |
| | | | |
| | == References == | | == References == |
| − |
| |
| − | * Konyagin, Sergei and Igor Shparlinski. 1999. ''Character Sums with Exponential Functions and their Applications''. Cambridge, UK: Cambridge University Press. ISBN 0521642639.
| |
| − | * Fried, H.M. 2002. ''Green's Functions and Ordered Exponentials''. Cambridge, UK: Cambridge University Press. ISBN 0521443903.
| |
| | * Carico, Charles C. 1974. ''Exponential and logarithmic functions (Wadsworth precalculus mathematics series)''. Belmont, CA: Wadsworth Pub. Co. ISBN 0534003141. | | * Carico, Charles C. 1974. ''Exponential and logarithmic functions (Wadsworth precalculus mathematics series)''. Belmont, CA: Wadsworth Pub. Co. ISBN 0534003141. |
| | + | * Fried, H. M. 2002. ''Green's Functions and Ordered Exponentials''. Cambridge, UK: Cambridge University Press. ISBN 0521443903. |
| | + | * Konyagin, Sergei, and Igor Shparlinski. 1999. ''Character Sums with Exponential Functions and their Applications''. Cambridge, UK: Cambridge University Press. ISBN 0521642639. |
| | | | |
| | ==External links== | | ==External links== |
| − | '''<<The first 3 links are created using a template form. In each case, please remove the template and replace it with the actual URL and name of Web site, putting them in square brackets, as done for the other Web links. Then add the Retrieved date.>>'''
| + | All links retrieved March 23, 2024. |
| | + | |
| | + | * [http://planetmath.org/?op=getobj&from=objects&id=6341 Complex exponential function]. |
| | + | * [http://planetmath.org/?op=getobj&from=objects&id=9313 Derivative of exponential function]. |
| | + | * [http://mathworld.wolfram.com/ExponentialFunction.html Exponential Function]. |
| | + | * [http://www.efunda.com/math/taylor_series/exponential.cfm Taylor Series Expansions of Exponential Functions] – efunda. |
| | | | |
| − | * [http://planetmath.org/?op=getobj&from=objects&id=6341 Complex exponential function]. Retrieved September 9, 2007.
| |
| − | * [http://planetmath.org/?op=getobj&from=objects&id=9313 Derivative of exponential function]. Retrieved September 9, 2007.
| |
| − | * Weisstein, Eric W. [http://mathworld.wolfram.com/ExponentialFunction.html Exponential Function]. Retrieved September 9, 2007.
| |
| − | * Mathews, John H. [http://math.fullerton.edu/mathews/c2003/ComplexFunExponentialMod.html Complex Exponential Function Module]. Retrieved September 9, 2007.
| |
| − | * [http://www.efunda.com/math/taylor_series/exponential.cfm Taylor Series Expansions of Exponential Functions]. efunda. Retrieved September 9, 2007.
| |
| − | * [http://www-math.mit.edu/daimp/ComplexExponential.html Complex exponential interactive graphic]. Retrieved September 9, 2007.
| |
| | | | |
| | [[Category:Physical sciences]] | | [[Category:Physical sciences]] |
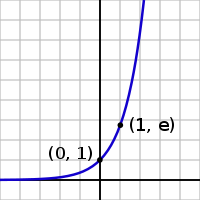
Graph of
y =
ex. The exponential function is nearly flat (climbing slowly) for negative values of
x, climbs quickly for positive values of
x, and equals 1 when
x is equal to 0. Its
y value always equals the slope at that point.
The exponential function is one of the most important functions in mathematics. For a variable x, this function is written as exp(x) or ex, where e is a mathematical constant, the base of the natural logarithm, which equals approximately 2.718281828, and is also known as Euler's number. Here, e is called the base and x is called the exponent. In a more general form, an exponential function can be written as ax, where a is a constant and x is a variable.
The graph of y = ex is shown on the right. The graph is always positive (above the x axis) and increases from left to right. It never touches the x axis, although it gets extremely close to it. In other words, the x axis is a horizontal asymptote to the graph. Its inverse function, the logarithm,  , is defined for all positive x.
, is defined for all positive x.
Sometimes, especially in the sciences, the term exponential function is more generally used for functions of the form kax, where a is any positive real number not equal to one.
In general, the variable x can be any real or complex number, or even an entirely different kind of mathematical object.
Some applications of the exponential function include modeling growth in populations, economic changes, fatigue of materials, and radioactive decay.
Properties
Most simply, exponential functions multiply at a constant rate. For example the population of a bacterial culture that doubles every 20 minutes can be expressed (approximatively, as this is not really a continuous problem) as an exponential, as can the value of a car that decreases by 10 percent per year.
Using the natural logarithm, one can define more general exponential functions. The function

defined for all a > 0, and all real numbers x, is called the exponential function with base a. Note that this definition of  rests on the previously established existence of the function
rests on the previously established existence of the function  , defined for all real numbers.
, defined for all real numbers.
Exponential functions "translate between addition and multiplication" as is expressed in the first three and the fifth of the following exponential laws:






These are valid for all positive real numbers a and b and all real numbers x and y. Expressions involving fractions and roots can often be simplified using exponential notation:

and, for any a > 0, real number b, and integer n > 1:
![{\displaystyle \,{\sqrt[{n}]{a^{b}}}=\left({\sqrt[{n}]{a}}\right)^{b}=a^{b/n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/329f4307f90537b8809943c47601795b1a5ed5c8)
Formal definition
The exponential function ex can be defined in a variety of equivalent ways, as an infinite series. In particular, it may be defined by a power series:

or as the limit of a sequence:

In these definitions, n! stands for the factorial of n, and x can be any real number, complex number, element of a Banach algebra (for example, a square matrix), or member of the field of p-adic numbers.
Derivatives and differential equations
The importance of exponential functions in mathematics and the sciences stems mainly from properties of their derivatives. In particular,

That is, ex is its own derivative. Functions of the form  for constant K are the only functions with that property. (This follows from the Picard-Lindelöf theorem, with
for constant K are the only functions with that property. (This follows from the Picard-Lindelöf theorem, with  and
and  .) Other ways of saying the same thing include:
.) Other ways of saying the same thing include:
- The slope of the graph at any point is the height of the function at that point.
- The rate of increase of the function at x is equal to the value of the function at x.
- The function solves the differential equation
 .
.
- exp is a fixed point of derivative as a functional
In fact, many differential equations give rise to exponential functions, including the Schrödinger equation and the Laplace's equation as well as the equations for simple harmonic motion.
For exponential functions with other bases:

Thus any exponential function is a constant multiple of its own derivative.
If a variable's growth or decay rate is proportional to its size—as is the case in unlimited population growth (see Malthusian catastrophe), continuously compounded interest, or radioactive decay—then the variable can be written as a constant times an exponential function of time.
Furthermore for any differentiable function f(x), we find, by the chain rule:
 .
.
Double exponential function
The term double exponential function can have two meanings:
- a function with two exponential terms, with different exponents
- a function
 ; this grows even faster than an exponential function; for example, if a = 10: f(−1) = 1.26, f(0) = 10, f(1) = 1010, f(2) = 10100 = googol, ..., f(100) = googolplex.
; this grows even faster than an exponential function; for example, if a = 10: f(−1) = 1.26, f(0) = 10, f(1) = 1010, f(2) = 10100 = googol, ..., f(100) = googolplex.
Factorials grow faster than exponential functions, but slower than double-exponential functions. Fermat numbers, generated by  and double Mersenne numbers generated by
and double Mersenne numbers generated by  are examples of double exponential functions.
are examples of double exponential functions.
See also
References
ISBN links support NWE through referral fees
- Carico, Charles C. 1974. Exponential and logarithmic functions (Wadsworth precalculus mathematics series). Belmont, CA: Wadsworth Pub. Co. ISBN 0534003141.
- Fried, H. M. 2002. Green's Functions and Ordered Exponentials. Cambridge, UK: Cambridge University Press. ISBN 0521443903.
- Konyagin, Sergei, and Igor Shparlinski. 1999. Character Sums with Exponential Functions and their Applications. Cambridge, UK: Cambridge University Press. ISBN 0521642639.
External links
All links retrieved March 23, 2024.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article
in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.












![{\displaystyle \,{\sqrt[{n}]{a^{b}}}=\left({\sqrt[{n}]{a}}\right)^{b}=a^{b/n}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/329f4307f90537b8809943c47601795b1a5ed5c8)











