Penrose triangle
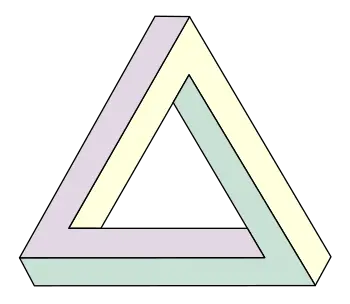
The Penrose triangle, also known as the tribar or impossible triangle, is an impossible object, first created by the Swedish artist Oscar Reutersvärd, popularized by Roger Penrose, and later featured prominently in the works of artist M. C. Escher. Impossible figures, such as the impossible cube and blivet, are a special class of ambiguous figures in which parts of the picture that are not ambiguous are drawn in incompatible perspectives. Ambiguous figures are those that, for the viewer, flip back and forth between equally possible perspectives of the object represented. The Necker cube is a well-known example of such an ambiguous drawing in which the perspective changes while viewing the figure.
Impossible figures like the Penrose triangle provide opportunities both for valuable research into human perceptual processes and to bring joy and fascination to many through their inclusion in works of art. Such artworks reveal humankind's endless fascination with the creative and unusual. These instances can also help us realize that our own perceptions may be limited or different from those of another person viewing the same thing.
Discovery
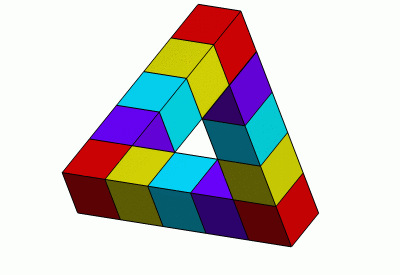
The Penrose triangle was first created by Swedish artist Oscar Reutersvärd in 1934. Known as the "father of impossible figures," Reutersvärd created the first Penrose triangle out an arrangement of cubes. In 1982, the Swedish government celebrated Reutersvärd's creation by putting it on a postage stamp.
It was not until 1954, when physicist Roger Penrose attended a lecture by artist M. C. Escher, that the Penrose triangle received widespread attention. Wanting to create something to illustrate impossibility in its purist form, Penrose created a perspective line drawing of an impossible triangle, which he published in a 1958 article in the British Journal of Psychology. It is important to note that, at this point, Escher had not yet created his three impossible prints (Belvedere, Ascending and Descending, and Waterfall). Penrose was also unfamiliar with the work of Reutersvärd and others in the field of impossible objects. Penrose's article, which was co-authored with his father, did much to create the popularity of the triangle.
A copy of the article was sent to Escher, who used it as inspiration to create the famous lithograph Waterfall.[1] The lithograph depicts a watercourse that flows in a zigzag along the long sides of two elongated Penrose triangles, so that it ends up two stories higher than it began. The resulting waterfall, forming the short sides of both triangles, drives a water wheel.
Description
At first glance, the Penrose triangle appears to be a two dimensional depiction of a three dimensional triangle built from square beams. However, the properties of this two dimensional drawing cannot be realized by any three dimensional object. Hence, the Penrose triangle is an "impossible object."
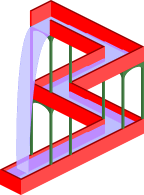
It is, however, possible to create a three dimensional object that looks like the two dimensional representation from a certain viewing direction only.[2][3] Interestingly, even when the viewer has seen the object from other angles and so is fully aware that the figure is not "impossible," perception from the critical viewing angle does not change‚ÄĒthe figure is still seen as impossible.[4]
Explanation
The illusion plays on the human eye's interpretation of two-dimensional pictures as three-dimensional objects. Visual perspective is twisted and used to create the illusion of a three dimensional object that cannot possibly exist. The problem arises because the viewer assumes that the features of the figure that are touching in the two dimensional representation are at the same distance from the viewer. The use of perspective to create depth adds to the effect of the illusion.
Applications
The Penrose triangle has inspired a number of artists. M.C. Escher's lithograph Waterfall depicts a watercourse that flows in a zigzag along the long sides of two elongated Penrose triangles, so that it ends up two stories higher than it began. The resulting waterfall, forming the short sides of both triangles, drives a water wheel. (Escher helpfully points out that in order to keep the wheel turning some water must occasionally be added to compensate for evaporation.)
The Penrose triangle has also inspired sculptures. In a sculpture in East Perth, Australia, there is a sculpture that, when viewed from one of two specific vantage points, appears to be a physical, three dimensional Penrose triangle. In reality, the sculpture is disjointed and only appears to be an impossible object.
There exists some terminological confusion over whether "Penrose triangle" refers to the two-dimensional depiction of an impossible three-dimensional object, or the impossible object itself. (Philosophically, it is unclear what "the impossible object" refers to, other than a set of conditions that cannot be satisfied.)
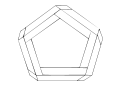
Other Penrose polygons
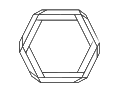
While it is possible to construct a Penrose triangle with other regular polygons to create a Penrose polygon, the visual effect is not as striking, and as the sides increase, the image seems to be warped or twisted. The Penrose triangle remains the strongest and most popular of this type of impossible object.
Penrose hexagon
Notes
- ‚ÜĎ Waterfall (1961) by Maurits Cornelis Escher Artchive. Retrieved March 17, 2024.
- ‚ÜĎ Gershon Elber, Escher for Real. Retrieved April 17, 2024.
- ‚ÜĎ Gershon Elber, Beyond Escher for Real. Retrieved April 17, 2024.
- ‚ÜĎ Richard L. Gregory, Eye and Brain. (Princeton, NJ: Princeton University Press, 1997, ISBN 0691048371), 239.
- ‚ÜĎ Impossible triangle in Perth (Australia). Impossible World. Retrieved March 17, 2024.
ReferencesISBN links support NWE through referral fees
- Gregory, Richard L. Eye and Brain. Princeton, NJ: Princeton University Press, 1997. ISBN 0691048371
- Huggett, S.A., L.J. Mason, K.P. Tod, S.T. Tsou, and N.M.J.Woodhouse (eds.). The Geometric Universe: Science, Geometry, and the Work of Roger Penrose . Oxford University Press, 1998. ISBN 0198500599
- Penrose, Roger, Abner Shimony, Nancy Cartwright, and Stephen Hawing. The Large, the Small and the Human Mind. Cambridge University Press, 2000. ISBN 0521785723
- Schattschneider, Doris, and Michele Emmer (eds.). M.C.Escher's Legacy: A Centennial Celebration. Springer, 2005. ISBN 3540201009
External links
All links retrieved March 17, 2024.
- Impossible Triangle The Centre for the Study of Perceptual Experience (CSPE)
- The Impossible Solid Rotating Penrose Triangle
- Penrose Triangle Wolfram MathWorld
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.