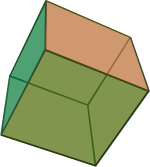
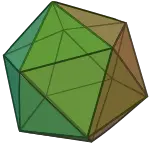
Polyhedron

Some Polyhedra dodecahedron (Regular polyhedron) Small stellated dodecahedron (Regular star) Icosidodecahedron (Uniform) Great cubicuboctahedron (Uniform star) Rhombic triacontahedron (Uniform dual) Elongated pentagonal cupola (Convex regular-faced) Octagonal prism (Uniform prism) Square antiprism (Uniform antiprism)

In geometry, a polyhedron (plural polyhedra or polyhedrons) is often defined as a three-dimensional object with flat, polygonal faces and straight edges. In this sense, it is a three-dimensional example of the more general structure called a polytope, which can have any number of dimensions. Cubes, prisms, and pyramids are examples of polyhedra.

A polyhedron surrounds a bounded volume in three-dimensional space; sometimes this interior volume is considered to be part of the polyhedron, sometimes only the surface is considered, and occasionally only the skeleton of edges. A polyhedron is said to be convex if its surface (comprising its faces, edges and corners) does not intersect itself and the line segment joining any two points of the polyhedron is contained in the interior and surface. A regular polyhedron is one in which the faces are regular polygons that are all congruent (exactly alike) and assembled in the same way around each vertex (corner).

More generally, in mathematics and other disciplines, the term polyhedron is used to refer to a variety of related constructs, some geometric and others purely algebraic or abstract. For this reason, modern mathematicians find that the above definition of a polyhedron is not very precise, yet they do not agree on the exact definition.

Etymology

The word polyhedron comes from the Classical Greek word πολυεδρον. It is a combination of poly, stem of πολυς meaning "many;" and -edron, form of εδρον meaning "base" or "seat" or "face."

Naming polyhedra

Polyhedra are often named according to the number of faces, based on classical Greek terms for the numbers. Examples are: tetrahedron (4), pentahedron (5), hexahedron (6), heptahedron (7), triacontahedron (30), and so on.

Often this name is qualified by a description of the kinds of faces present; for example, the rhombic dodecahedron versus the pentagonal dodecahedron.

Other common names indicate that some operation has been performed on a simpler polyhedron. For example, the truncated cube looks like a cube with its corners cut off, and has 14 faces (so it is also an example of a tetrakaidecahedron).

Some special polyhedra have been given their own names over the years, such as Miller's monster or the Szilassi polyhedron.

Characteristics

The three-dimensional body of a polyhedron is made up of several components: The faces are parts of two-dimensional planes that meet in pairs along the edges (which are one-dimensional straight-line segments), and the edges meet in points called vertices (which are zero-dimensional).

A defining characteristic of almost all kinds of polyhedra is that just two faces join along any common edge. This ensures that the polyhedral surface is continuously connected and does not end abruptly or split off in different directions.

Edges Edges have two important characteristics (unless the polyhedron is complex):

• An edge joins just two vertices
• An edge joins just two faces

These two characteristics are dual to each other.

Euler characteristic The Euler characteristic χ relates the number of vertices V, edges E, and faces F of a polyhedron:

χ = V - E + F

For a simply connected polyhedron χ = 2.

Duality

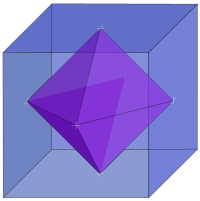
For every polyhedron, there is a dual polyhedron having faces in place of the original's vertices, and vice versa. For example, the dual polyhedron of a cube is an octahedron. (In most cases, the dual can be obtained by the process of spherical reciprocation.)

Vertex figure For every vertex one can define a vertex figure consisting of the vertices joined to it. The vertex is said to be regular if this is a regular polygon and symmetrical with respect to the whole polyhedron.

Traditional polyhedra

A square pyramid is an historical example of a polyhedron. It is not, however, a symmetrical polyhedron, because the square base differs from the triangular sides.

Symmetrical polyhedra

Many of the most studied polyhedra are highly symmetrical.

Of course, it is easy to distort such polyhedra so they are no longer symmetrical. But where a polyhedral name is given, such as icosidodecahedron, the most symmetrical geometry is almost always implied, unless otherwise stated.

Some of the most common names, in particular, are often used with "regular" in front or implied because for each there are different types which have little in common except for having the same number of faces. These are the tetrahedron, cube, octahedron, dodecahedron, and icosahedron:

Polyhedra of the highest symmetries have all of some kind of element—faces, edges, and/or vertices, within a single symmetry orbit. There are various classes of such polyhedra:

• Isogonal or Vertex-transitive if all vertices are the same, in the sense that for any two vertices there exists a symmetry of the polyhedron mapping the first isometrically onto the second.
• Isotoxal or Edge-transitive if all edges are the same, in the sense that for any two edges there exists a symmetry of the polyhedron mapping the first isometrically onto the second.
• Isohedral or Face-transitive if all faces are the same, in the sense that for any two faces there exists a symmetry of the polyhedron mapping the first isometrically onto the second.
• Regular if it is vertex-transitive, edge-transitive, and face-transitive (this implies that every face is the same regular polygon; it also implies that every vertex is regular).
• Quasi-regular if it is vertex-transitive and edge-transitive (and hence has regular faces) but not face-transitive. A quasi-regular dual is face-transitive and edge-transitive (and hence every vertex is regular) but not vertex-transitive.
• Semi-regular if it is vertex-transitive but not edge-transitive, and every face is a regular polygon. (This is one of several definitions of the term, depending on author. Some definitions overlap with the quasi-regular class). A semi-regular dual is face-transitive but not vertex-transitive, and every vertex is regular.
• Uniform if it is vertex-transitive and every face is a regular polygon, that is, it is regular, quasi-regular or semi-regular. A uniform dual is face-transitive and has regular vertices, but is not necessarily vertex-transitive).
• Noble if it is face-transitive and vertex-transitive (but not necessarily edge-transitive). The regular polyhedra are also noble; they are the only noble uniform polyhedra.

A polyhedron can belong to the same overall symmetry group as one of higher symmetry, but will have several groups of elements (for example, faces) in different symmetry orbits.

Uniform polyhedra and their duals

Uniform polyhedra are vertex-transitive and every face is a regular polygon. They may be regular, quasi-regular, or semi-regular, and may be convex or starry.

The uniform duals are face-transitive and every vertex figure is a regular polygon.

Face-transitivity of a polyhedron corresponds to vertex-transitivity of the dual and conversely, and edge-transitivity of a polyhedron corresponds to edge-transitivity of the dual. In most duals of uniform polyhedra, faces are irregular polygons. The regular polyhedra are an exception, because they are dual to each other.

Each uniform polyhedron shares the same symmetry as its dual, with the symmetries of faces and vertices simply swapped over. Because of this some authorities regard the duals as uniform too. But this idea is not held widely: A polyhedron and its symmetries are not the same thing.

The uniform polyhedra and their duals are traditionally classified according to their degree of symmetry, and whether they are convex or not.

	Convex uniform	Convex uniform dual	Star uniform	Star uniform dual
Regular	Platonic solids		Kepler-Poinsot polyhedra
Quasiregular	Archimedean solids	Catalan solids	(no special name)	(no special name)
Semiregular			(no special name)	(no special name)
	Prisms	Dipyramids	Star Prisms	Star Dipyramids
	Antiprisms	Trapezohedra	Star Antiprisms	Star Trapezohedra

Noble polyhedra

A noble polyhedron is both isohedral (equal-faced) and isogonal (equal-cornered). Besides the regular polyhedra, there are many other examples.

The dual of a noble polyhedron is also noble.

Symmetry groups

The polyhedral symmetry groups are all point groups and include:

• T—chiral tetrahedral symmetry; the rotation group for a regular tetrahedron; order 12.
• T_d—full tetrahedral symmetry; the symmetry group for a regular tetrahedron; order 24.
• T_h—pyritohedral symmetry; order 24. The symmetry of a pyritohedron.
• O—chiral octahedral symmetry; the rotation group of the cube and octahedron; order 24.
• O_h—full octahedral symmetry; the symmetry group of the cube and octahedron; order 48.
• I—chiral icosahedral symmetry; the rotation group of the icosahedron and the dodecahedron; order 60.
• I_h—full icosahedral symmetry; the symmetry group of the icosahedron and the dodecahedron; order 120.
• C_nv—n-fold pyramidal symmetry
• D_nh—n-fold prismatic symmetry
• D_nv—n-fold antiprismatic symmetry

Those with chiral symmetry do not have reflection symmetry and hence have two enantiomorphous forms which are reflections of each other. The snub Archimedean polyhedra have this property.

Other polyhedra with regular faces

Equal regular faces

A few families of polyhedra, where every face is the same kind of polygon:

• Deltahedra have equilateral triangles for faces.
• With regard to polyhedra whose faces are all squares: if coplanar faces are not allowed, even if they are disconnected, there is only the cube. Otherwise there is also the result of pasting six cubes to the sides of one, all seven of the same size; it has 30 square faces (counting disconnected faces in the same plane as separate). This can be extended in one, two, or three directions: we can consider the union of arbitrarily many copies of these structures, obtained by translations of (expressed in cube sizes) (2,0,0), (0,2,0), and/or (0,0,2), hence with each adjacent pair having one common cube. The result can be any connected set of cubes with positions (a, b, c), with integers a, b, c, of which at most one is even.
• There is no special name for polyhedra whose faces are all equilateral pentagons or pentagrams. There are infinitely many of these, but only one is convex: The dodecahedron. The rest are assembled by (pasting) combinations of the regular polyhedra described earlier: The dodecahedron, the small stellated dodecahedron, the great stellated dodecahedron and the great icosahedron.

There exists no polyhedron whose faces are all identical and are regular polygons with six or more sides because the vertex of three regular hexagons defines a plane.

Deltahedra

A deltahedron (plural deltahedra) is a polyhedron whose faces are all equilateral triangles. There are infinitely many deltahedra, but only eight of these are convex:

• 3 regular convex polyhedra (3 of the Platonic solids)
  • Tetrahedron
  • Octahedron
  • Icosahedron
• 5 non-uniform convex polyhedra (5 of the Johnson solids)
  • Triangular dipyramid
  • Pentagonal dipyramid
  • Snub disphenoid
  • Triaugmented triangular prism
  • Gyroelongated square dipyramid

Johnson solids

Norman Johnson sought which non-uniform polyhedra had regular faces. In 1966, he published a list of 92 convex solids, now known as the Johnson solids, and gave them their names and numbers. He did not prove there were only 92, but he did conjecture that there were no others. Victor Zalgaller in 1969 proved that Johnson's list was complete.

Other important families of polyhedra

Pyramids

Pyramids include some of the most time-honored and famous of all polyhedra. A pyramid is any three-dimensional structure where the upper surfaces are triangular and converge on one point (apex). The base of the pyramid is usually quadrilateral or trilateral (but generally may be of any polygon shape), meaning that a pyramid usually has four or three sides. The measurements of these triangles uniformly classify the shape as isosceles and sometimes equilateral.

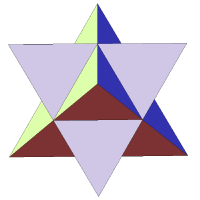
Stellation and faceting

Stellation of a polyhedron is the process of extending the faces (within their planes) so that they meet to form a new polyhedron.

It is the converse of faceting, which is the process of removing parts of a polyhedron without creating any new vertices.

Zonohedra

A zonohedron is a convex polyhedron where every face is a polygon with inversion symmetry or, equivalently, symmetry under rotations through 180°.

Compounds

Polyhedral compounds are formed as compounds of two or more polyhedra.

These compounds often share the same vertices as other polyhedra and are often formed by stellation. Some are listed in the list of Wenninger polyhedron models.

Orthogonal polyhedra

An orthogonal polyhedron is one all of whose faces meet at right angles, and all of whose edges are parallel to axes of a Cartesian coordinate system. Aside from a rectangular box, orthogonal polyhedra are nonconvex. They are the 3D analogs of 2D orthogonal polygons (also known as rectilinear polygons). Orthogonal polyhedra are used in computational geometry, where their constrained structure has enabled advances on problems unsolved for arbitrary polyhedra, for example, unfolding the surface of a polyhedron to a net (polyhedron).

Generalizations of polyhedra

The name "polyhedron" has come to be used for a variety of objects having similar structural properties to traditional polyhedra.

Apeirohedra

A classical polyhedral surface comprises finite, bounded plane regions, joined in pairs along edges. If such a surface extends indefinitely it is called an apeirohedron. Examples include:

• Tilings or tessellations of the plane.
• Sponge-like structures called infinite skew polyhedra.

Complex polyhedra

A complex polyhedron is one which is constructed in unitary 3-space. This space has six dimensions: three real ones corresponding to ordinary space, with each accompanied by an imaginary dimension.

Curved polyhedra

In some fields of study, polyhedra may have curved faces and edges.

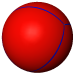
Spherical polyhedra

The surface of a sphere may be divided by line segments into bounded regions to form spherical tiling, and the sphere is called a spherical polyhedron. Much of the theory of symmetrical polyhedra is most conveniently derived in this way.

Spherical polyhedra have a long history:

• The first known man-made polyhedra were spherical polyhedra carved in stone. Many have been found in Scotland and appear to date from the neolithic period (the New Stone Age).
• At the start of the nineteenth century, Louis Poinsot used spherical polyhedra to discover the four regular star polyhedra.
• In the middle of the twentieth century, Harold Scott MacDonald Coxeter used them to enumerate all but one of the uniform polyhedra, through the construction of kaleidoscopes (Wythoff construction).

Some polyhedra—such as the hosohedra and their duals the dihedra—exist as spherical polyhedra but have no flat-faced analog. In the examples below, {2, 6} is a hosohedron and {6, 2} is a dual dihedron.

All the regular and semiregular polyhedra can be projected onto a sphere as tilings. Some examples follow, given by their Schläfli symbol {p, q} or vertex figure (a.b.c. …):

Tetrahedral (3 3 2)	{3,3}	(3.6.6)	(3.3.3.3)	(3.6.6)	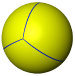{3,3}	(3.4.3.4)	(4.6.6)
Octahedral (4 3 2)	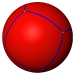{4,3}	(3.8.8)	(3.4.3.4)	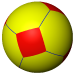(4.6.6)	{3,4}	(3.4.4.4)	(4.6.8)
Icosahedral (5 3 2)	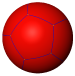{5,3}	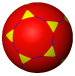(3.10.10)	(3.5.3.5)	(5.6.6)	{3,5}	(3.4.5.4)	(4.6.10)
Dihedral (6 2 2) example	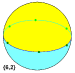{6,2}		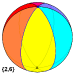		{2,6}

Curved, space-filling polyhedra

Two important types are:

• Bubbles in froths and foams.
• Spacefilling forms used in architecture.

General polyhedra

More recently mathematics has defined a polyhedron as a set in real affine (or Euclidean) space of any dimensional n that has flat sides. It could be defined as the union of a finite number of convex polyhedra, where a convex polyhedron is any set that is the intersection of a finite number of half-spaces. It may be bounded or unbounded. In this meaning, a polytope is a bounded polyhedron.

All traditional polyhedra are general polyhedra. Additional examples are:

• A quadrant in the plane. For instance, the region of the cartesian plane consisting of all points above the horizontal axis and to the right of the vertical axis: { ( x, y ) : x ≥ 0, y ≥ 0 }. Its sides are the two positive axes.
• An octant in Euclidean 3-space, { ( x, y, z ) : x ≥ 0, y ≥ 0, z ≥ 0 }.
• A prism of infinite extent. For instance a doubly-infinite square prism in 3-space, consisting of a square in the xy-plane swept along the z-axis: { ( x, y, z ) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 }.
• Each cell in a Voronoi tessellation is a convex polyhedron. In the Voronoi tessellation of a set S, the cell A corresponding to a point c∈S is bounded (hence a traditional polyhedron) when c lies in the interior of the convex hull of S, and otherwise (when c lies on the boundary of the convex hull of S) A is unbounded.

Hollow-faced or skeletal polyhedra

It is not necessary to fill in the face of a figure before one can call it a polyhedron. For example, Leonardo da Vinci devised frame models of the regular solids, which he drew for Pacioli's book Divina Proportione. In modern times, Branko Grünbaum (1994) made a special study of this class of polyhedra, in which he developed an early idea of abstract polyhedra. He defined a face as a cyclically ordered set of vertices, and allowed faces to be skew as well as planar.

Tessellations or tilings

Tessellations or tilings of the plane are sometimes treated as polyhedra, because they have quite a lot in common. For example the regular ones can be given Schläfli symbols.

Non-geometric polyhedra

Various mathematical constructs have been found to have properties also present in traditional polyhedra.

Topological polyhedra

A topological polytope is a topological space given along with a specific decomposition into shapes that are topologically equivalent to convex polytopes and that are attached to each other in a regular way.

Such a figure is called simplicial if each of its regions is a simplex, that is, in an n-dimensional space each region has n+1 vertices. The dual of a simplicial polytope is called simple. Similarly, a widely studied class of polytopes (polyhedra) is that of cubical polyhedra, when the basic building block is an n-dimensional cube.

Abstract polyhedra

An abstract polyhedron is a partially ordered set (poset) of elements. Theories differ in detail, but essentially the elements of the set correspond to the body, faces, edges, and vertices of the polyhedron. The empty set corresponds to the null polytope, or nullitope, which has a dimensionality of -1. These posets belong to the larger family of abstract polytopes in any number of dimensions.

Polyhedra as graphs

Any polyhedron gives rise to a graph, or skeleton, with corresponding vertices and edges. Thus graph terminology and properties can be applied to polyhedra. For example:

• Due to Steinitz theorem convex polyhedra are in one-to-one correspondence with 3-connected planar graphs.
• The tetrahedron gives rise to a complete graph (K₄). It is the only polyhedron to do so.
• The octahedron gives rise to a strongly regular graph, because adjacent vertices always have two common neighbors, and non-adjacent vertices have four.
• The Archimedean solids give rise to regular graphs: 7 of the Archimedean solids are of degree 3, 4 of degree 4, and the remaining 2 are chiral pairs of degree 5.

History

Prehistory

Stones carved in shapes showing the symmetries of various polyhedra have been found in Scotland and may be as much a 4,000 years old. These stones show not only the form of various symmetrical polyehdra, but also the relations of duality amongst some of them (that is, that the centers of the faces of the cube gives the vertices of an octahedron, and so on). Examples of these stones are on display in the John Evans room of the Ashmolean Museum at Oxford University. It is impossible to know why these objects were made, or how the sculptor gained the inspiration for them.

Other polyhedra have, of course, made their mark in architecture—cubes and cuboids being obvious examples, with the earliest four-sided pyramids of ancient Egypt also dating from the Stone Age.

The Etruscans preceded the Greeks in their awareness of at least some of the regular polyhedra, as evidenced by the discovery near Padua (in Northern Italy) in the late 1800s of a dodecahedron made of soapstone, and dating back more than 2,500 years (Lindemann, 1987). Pyritohedric crystals are found in northern Italy.

Greeks

The earliest known written records of these shapes come from Classical Greek authors, who also gave the first known mathematical description of them. The earlier Greeks were interested primarily in the convex regular polyhedra, while Archimedes later expanded his study to the convex uniform polyhedra.

Muslims and Chinese

After the end of the Classical era, Islamic scholars continued to make advances, for example in the tenth century Abu'l Wafa described the convex regular and quasiregular spherical polyhedra. Meanwhile in China, dissection of the cube into its characteristic tetrahedron (orthoscheme) and related solids was used as the basis for calculating volumes of earth to be moved during engineering excavations.

Renaissance

Much to be said here: Piero della Francesca, Pacioli, Leonardo Da Vinci, Wenzel Jamnitzer, Durer, and so on, leading up to Kepler.

Star polyhedra

For almost 2000 years, the concept of a polyhedron had remained as developed by the ancient Greek mathematicians.

Johannes Kepler realized that star polygons could be used to build star polyhedra, which have non-convex regular polygons, typically pentagrams as faces. Some of these star polyhedra may have been discovered before Kepler's time, but he was the first to recognize that they could be considered "regular" if one removed the restriction that regular polytopes be convex. Later, Louis Poinsot realised that star vertex figures (circuits around each corner) can also be used, and discovered the remaining two regular star polyhedra. Cauchy proved Poinsot's list complete, and Cayley gave them their accepted English names: (Kepler's) the small stellated dodecahedron and great stellated dodecahedron, and (Poinsot's) the great icosahedron and great dodecahedron. Collectively, they are called the Kepler-Poinsot polyhedra.

The Kepler-Poinsot polyhedra may be constructed from the Platonic solids by a process called stellation. Most stellations are not regular. The study of stellations of the Platonic solids was given a big push by H. S. M. Coxeter and others in 1938, with the now famous paper The 59 icosahedra. This work has recently been re-published (Coxeter, 1999).

The reciprocal process to stellation is called facetting (or faceting). Every stellation of one polytope is dual, or reciprocal, to some facetting of the dual polytope. The regular star polyhedra can also be obtained by facetting the Platonic solids. Bridge 1974 listed the simpler facetings of the dodecahedron, and reciprocated them to discover a stellation of the icosahedron that was missing from the famous "59." More have been discovered since.

Regular polyhedra

A regular polyhedron is a polyhedron whose faces are congruent (all alike) regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive, and face-transitive—that is, it is transitive on its flags. This last alone is a sufficient definition.

A regular polyhedron is identified by its Schläfli symbol of the form {n, m}, where n is the number of sides of each face and m the number of faces meeting at each vertex.

The nine regular polyhedra

There are five convex regular polyhedra, known as the Platonic solids:

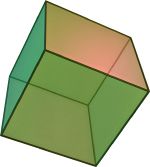
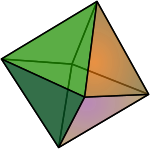
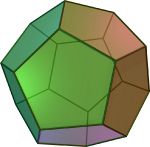
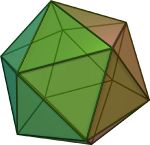
Tetrahedron {3, 3}	Cube {4, 3}	Octahedron {3, 4}	Dodecahedron {5, 3}	Icosahedron {3, 5}

There are also four regular star polyhedra, the Kepler-Poinsot polyhedra:

Small stellated dodecahedron {5/2, 5}	Great stellated dodecahedron {5/2, 3}	Great dodecahedron {5, 5/2}	Great icosahedron {3, 5/2}

Characteristics

Equivalent properties The property of having a similar arrangement of faces around each vertex can be replaced by any of the following equivalent conditions in the definition:

• The vertices of the polyhedron all lie on a sphere
• All the dihedral angles of the polyhedron are equal
• All the vertex figures of the polyhedron are regular polygons
• All the solid angles of the polyhedron are congruent (Cromwell, 1997)

Concentric spheres A regular polyhedron has all of three related spheres (other polyhedra lack at least one kind) which share its centre:

• An insphere, tangent to all faces
• An intersphere or midsphere, tangent to all edges
• A circumsphere, tangent to all vertices

Symmetry The regular polyhedra are the most symmetrical of all the polyhedra. They lie in just three symmetry groups, which are named after them:

• Tetrahedral
• Octahedral (or cubic)
• Icosahedral (or dodecahedral)

Euler characteristic The five Platonic solids have an Euler characteristic of 2. Some of the regular stars have a different value.

Duality of regular polyhedra

The regular polyhedra come in natural pairs, with each twin being dual to the other (that is, the vertices of one polyhedron correspond to the faces of the other, and vice versa):

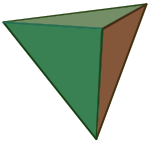
• The tetrahedron is self dual, i.e. it pairs with itself
• The cube and octahedron are dual to each other
• The icosahedron and dodecahedron are dual to each other
• The small stellated dodecahedron and great dodecahedron are dual to each other
• The great stellated dodecahedron and great icosahedron are dual to each other

The Schläfli symbol of the dual is just the original written backwards, for example the dual of {5, 3} is {3, 5}.

History of regular polyhedra

Prehistory

Stones carved in shapes showing the symmetry of all five of the Platonic solids have been found in Scotland and may be as much as 4,000 years old. These stones show not only the form of each of the five Platonic solids, but also the relations of duality amongst them (that is, that the centres of the faces of the cube gives the vertices of an octahedron, and so on). Examples of these stones are on display in the John Evans room of the Ashmolean Museum at Oxford University. It is impossible to know why these objects were made, or how the sculptor gained the inspiration for them.

It is also possible that the Etruscans preceded the Greeks in their awareness of at least some of the regular polyhedra, as evidenced by the discovery near Padua (in Northern Italy) in the late 1800s, of a dodecahedron made of soapstone, and dating back more than 2,500 years (Lindemann, 1987).

Greeks

The Greeks were the first to make written records, including mathematical descriptions, of the regular Platonic solids. Some authors (Sanford, 1930) credit Pythagoras (550 B.C.E.) with being familiar with them all. Others indicate that he may have been familiar with only the tetrahedron, cube, and dodecahedron, crediting the discovery of the other two to Theaetetus (an Athenian), who gave a mathematical description of all five (Van der Waerden, 1954), (Euclid, book XIII). H.S.M. Coxeter (Coxeter, 1948, Section 1.9) credits Plato (400 B.C.E.) with having made models of them, and mentions that one of the earlier Pythagoreans, Timaeus of Locri, used all five in a correspondence between the polyhedra and the nature of the universe as it was then perceived. This correspondence is recorded in Plato's dialogue Timaeus. It is from Plato's name that the term Platonic solids is derived.

Regular star polyhedra

For almost 2000 years, the concept of a regular polyhedron remained as developed by the ancient Greek mathematicians. One might characterize the Greek definition as follows:

• A regular polygon is a (convex) planar figure with all edges equal and all corners equal
• A regular polyhedron is a solid (convex) figure with all faces being congruent regular polygons, the same number arranged all alike around each vertex

This definition rules out, for example, the square pyramid (since although all the faces are regular, the square base is not congruent to the triangular sides), or the shape formed by joining two tetrahedra together (since although all faces would be equilateral triangles, that is, congruent and regular, some vertices have 3 triangles and others have 4).

However, in addition to the Platonic solids, the modern definition of regular polyhedra also includes the regular star polyhedra, otherwise known as the Kepler-Poinsot polyhedra, after Johannes Kepler and Louis Poinsot. Star polygons were first described in the fourteenth century by Thomas Bradwardine (Cromwell, 1997). Johannes Kepler realized that star polygons could be used to build star polyhedra, which have non-convex regular polygons, typically pentagrams as faces. Some of these star polyhedra may have been discovered by others before Kepler's time, but he was the first to recognize that they could be considered "regular" if one removed the restriction that regular polyhedra be convex. Later, Poinsot realized that star vertex figures (circuits around each corner) can also be used, and discovered the remaining two star polyhedra. Cayley gave them English names which have become accepted. They are: (Kepler's) the small stellated dodecahedron and great stellated dodecahedron, and (Poinsot's) the great icosahedron and great dodecahedron.

The Kepler-Poinsot polyhedra may be constructed from the Platonic solids by a process called stellation. The reciprocal process to stellation is called facetting (or faceting). Every stellation of one polyhedron is dual, or reciprocal, to some facetting of the dual polyhedron. The regular star polyhedra can also be obtained by facetting the Platonic solids. This was first done by Bertrand.

In ancient times, the Pythagoreans believed that there was a harmony between the regular polyhedra and the orbits of the planets. In the seventeenth century, Johannes Kepler studied data on planetary motion compiled by Tycho Brahe and for a decade tried to establish the Pythagorean ideal by finding a match between the sizes of the polyhedra and the sizes of the planets' orbits. His search failed in its original objective, but out of this research came his discoveries of the Kepler solids as regular polytopes, the realization that the orbits of planets are not circles, and the laws of planetary motion for which he is now famous. In Kepler's time, only five planets (excluding the Earth) were known, nicely matching the number of Platonic solids. Kepler's work, and the later discovery of Uranus, Neptune, and Pluto, have invalidated the Pythagorean idea.

Polyhedra in nature

Each of the Platonic solids occurs naturally in one form or other.

The tetrahedron, cube, and octahedron all occur as crystals. These by no means exhaust the numbers of possible forms of crystals (Smith, 1982, p. 212), of which there are 48. Neither the regular icosahedron nor the regular dodecahedron are among them, although one of the forms, called the pyritohedron, has twelve pentagonal faces arranged in the same pattern as the faces of the regular dodecahedron. The faces of the pyritohedron, however, are not regular, so the pyritohedron is not a regular structure.

Circogonia icosahedra, a species of Radiolaria.

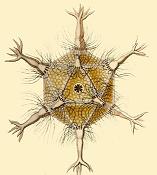
Polyhedra appear in biological systems as well. In the early twentieth century, Ernst Haeckel described a number of species of Radiolaria, and the skeletons of some of them are shaped like various regular polyhedra (Haeckel, 1904). Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus, and Circorrhegma dodecahedra; the shapes of these creatures are indicated by their names. The outer protein shells of many viruses form regular polyhedra. For example, HIV is enclosed in a regular icosahedron.

A more recent discovery is of a series of new forms of carbon, known as the fullerenes. Although C₆₀, the most easily produced fullerene, looks more or less spherical, some of the larger varieties (such as C₂₄₀, C₄₈₀ and C₉₆₀) are thought to take the form of slightly rounded icosahedra, a few nanometers across.

References

ISBN links support NWE through referral fees

• Arnone, Wendy. 2001. Geometry for Dummies. Hoboken, NJ: For Dummies (Wiley). ISBN 0764553240.
• Coxeter, H.S.M., M.S. Longuet-Higgins, and J.C.P. Miller. 1954. Phil. Trans. 246 (916): 401-50.
• Cromwell, Peter R. 1997. Polyhedra. Cambridge: Cambridge University Press. ISBN 0-521-66405-5.
• Haeckel, E. Art Forms in Nature. Prestel, 1998. ISBN 3-7913-1990-6.
• Hartshorne, Robin. 2002. Geometry: Euclid and Beyond. New York: Springer. ISBN 0387986502.
• Leff, Lawrence S. 1997. Geometry the Easy Way. Hauppauge, NY: Barron’s Educational Series. ISBN 0764101102.
• MacLean, Kenneth J.M. 2007. A Geometric Analysis of the Platonic Solids and Other Semi-Regular Polyhedra: With an Introduction to the Phi Ratio. Ann Arbor, MI: Loving Healing Press. ISBN 978-1932690996.
• Pearce, Peter. 1980. Structure in Nature is a Strategy for Design. Cambridge: MIT Press. ISBN 0262660458.
• Poinsot, Louis. 1810. Memoire sur les polygones et polyèdres. J. de l'École Polytechnique 9:16-48.
• Smith, Joseph V. 1982. Geometrical and Structural Crystallography. New York: Wiley. ISBN 0471861685.
• Sommerville, D.M.Y. 1930. An Introduction to the Geometry of n Dimensions. New York: E.P. Dutton, 1958.
• Stillwell, John. 2005. The Four Pillars of Geometry. Undergraduate Texts in Mathematics. New York: Springer. ISBN 0387255303.
• Williams, Robert. 1979. The Geometrical Foundation of Natural Structure: A Source Book of Design. New York: Dover. ISBN 048623729X.

External links

All links retrieved November 24, 2022.

• Eric W. Weisstein. Polyhedron. MathWorld.
• Polyhedra Pages.
• The Uniform Polyhedra.
• Virtual Reality Polyhedra - The Encyclopedia of Polyhedra.
  • Polyhedra and Pyramids.
• Paper Models of Polyhedra Free nets of polyhedra.
• Paper Models of Uniform (and other) Polyhedra.
• Electronic Geometry Models - Contains a peer reviewed selection of polyhedra with unusual properties.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Polyhedron  ^history
• Regular_polyhedron  ^history
• Spherical_polyhedron  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Polyhedron"

Note: Some restrictions may apply to use of individual images which are separately licensed.