Difference between revisions of "Fuzzy logic" - New World Encyclopedia
Keisuke Noda (talk | contribs) |
Rosie Tanabe (talk | contribs) |
||
| (21 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{2Copyedited}}{{Ebcompleted}}{{Copyedited}}{{Paid}}{{Approved}}{{Images OK}}{{Submitted}} | ||
| + | '''Fuzzy logic''', when construed in a wider sense, is the theory of ''fuzzy sets''. The concept of fuzzy sets provides a convenient way to represent various notions with imprecision, vagueness, or fuzziness, for example young, tall, cold, and so forth, which we frequently employ in our everyday life. As such, fuzzy logic has the rationale of more closely resembling than traditional logic the way human beings actually think, where alternatives are not black and white but shades of gray. Fuzzy logic has had notable success in various engineering applications. | ||
| − | + | When construed in a narrower sense, fuzzy logic is an extension of ordinary two-valued logic in such a way that the points in interval units are allowed as truth-values. As the truth-values are generalized in such a way, usual truth-functional operations are generalized accordingly. | |
| + | {{toc}} | ||
| + | Fuzzy logic is controversial in some circles, despite wide acceptance and a broad track record of successful applications. It is rejected by some [[Control theory|control engineers]] for validation and other reasons, and by some [[statistics|statisticians]] who hold that [[probability]] is the only rigorous mathematical description of uncertainty. Critics also argue that it cannot be a superset of ordinary set theory since membership functions are defined in terms of conventional sets. | ||
| − | + | == Fuzzy Sets == | |
| + | Fuzzy logic studies fuzzy sets, which was first introduced by L. Zadeh in 1965. Zadeh maintains that the meanings of many words in natural language come with degrees. Twelve years old and 18 years old are clearly both young; however 12 years old is younger than 18 years old. To represent this, he introduces the concept of ''fuzzy subsets''. A fuzzy subset of a given set ''U'' is a function from ''U'' into [1, 0]. The value that a given fuzzy set ''A'' assigns to an element ''x'' in ''U'' is called ''the degree of the membership of x in the fuzzy set A''. Fuzzy subsets are usually referred to simply as ''fuzzy sets''. Using this framework, the meaning of, say, the word “young” can be represented. Take the set of natural numbers and define some fuzzy set, as you like, that assigns values in the unit interval to natural numbers so that, say, 12 (years old) get some value (e.g. .95) higher than the value that 18 (e.g. .85). In that case, the value that each number gets assigned represents the degree of youth. The degree of the membership of 12 in the “youth” subset is higher than that of 18. | ||
| − | + | This concept of fuzzy sets generalizes the concept of sets in ordinary set theory. Given a set ''U'', a subset ''S'', in the ordinary sense, of ''U'' are determined by a function from ''U'' to [1, 0]. The elements of ''U'' that get 1 assigned represent the elements in ''S'' and the elements that get 0 assigned represent the elements that are not in ''S''. The elements of ''U'' are all either in, or not in, the subset. However, fuzzy subsets are allowed to take any value in the unit interval other than just 1 and 0. In this sense, the sets in the ordinary sense are special cases of fuzzy sets. | |
| − | + | ==Applications in Engineering== | |
| − | == | + | ===Examples=== |
| − | Fuzzy logic can be used to | + | Fuzzy logic can be used to control household appliances such as washing machines (which sense load size and detergent concentration and adjust their wash cycles accordingly) and refrigerators. |
| − | A basic application might characterize subranges of a continuous variable. | + | A basic application might characterize subranges of a continuous variable. For instance, a temperature measurement for anti-lock brakes might have several separate membership functions defining particular temperature ranges needed to control the brakes properly. Each function maps the same temperature value to a truth value in the 0 to 1 range. These truth values can then be used to determine how the brakes should be controlled. |
[[Image:Warm_fuzzy_logic_member_function.gif|center]] | [[Image:Warm_fuzzy_logic_member_function.gif|center]] | ||
| − | In this image, ''cold'', ''warm'', and ''hot'' are functions mapping a temperature scale. A point on that scale has three "truth values" — one for each of the three functions. For the particular temperature shown, the three truth values could be interpreted as describing the temperature as, say, "fairly cold" | + | In this image, ''cold'', ''warm'', and ''hot'' are functions mapping a temperature scale. A point on that scale has three "truth values"—one for each of the three functions. For the particular temperature shown, the three truth values could be interpreted as describing the temperature as, say, "fairly cold," "slightly warm," and "not hot." |
| − | A more sophisticated practical example is the use of fuzzy logic in high-performance | + | A more sophisticated practical example is the use of fuzzy logic in high-performance error correction to improve information reception over a limited-bandwidth communication link affected by data-corrupting noise using turbo codes. The front-end of a decoder produces a likelihood measure for the value intended by the sender (0 or 1) for each bit in the data stream. The likelihood measures might use a scale of 256 values between extremes of "certainly 0" and "certainly 1." Two decoders may analyze the data in parallel, arriving at different likelihood results for the values intended by the sender. Each can then use as additional data the other's likelihood results, and repeats the process to improve the results until consensus is reached as to the most likely values. |
| − | == | + | === Other Examples === |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * Automobile and other vehicle subsystems, such as ABS and cruise control (e.g. Tokyo monorail) | |
| − | + | * Air conditioners | |
| − | * Automobile subsystems, such as | + | * The MASSIVE engine used in the ''Lord of the Rings'' films, which helped show huge scale armies create random, yet orderly movements |
| − | * | ||
| − | * The | ||
* [[Camera]]s | * [[Camera]]s | ||
| − | * | + | * Digital image processing, such as edge detection |
| − | * | + | * Rice cookers |
| − | * | + | * Dishwashers |
| − | * | + | * Elevators |
| − | * | + | * Washing machines and other home appliances |
| − | * | + | * Video game [[artificial intelligence]] |
| − | * | + | * Language filters on message boards and chat rooms for filtering out offensive text |
| + | * Pattern recognition in Remote Sensing | ||
| − | Fuzzy logic has also been incorporated into some | + | Fuzzy logic has also been incorporated into some microcontrollers and microprocessors, for instance, the Freescale 68HC12. |
| − | == | + | ==Formal Fuzzy Logics== |
| − | Fuzzy logic | + | Fuzzy logic, when narrowly construed, is an extension of ordinary logics. The basic idea is that, in fuzzy extensions of logics, formulas can take any values in the unit interval, instead of just 1 or 0 as in ordinary logics. |
| − | + | === Basic Fuzzy Propositional Logic === | |
| − | + | In ''basic fuzzy propositional logic'', formulas are built, as in the language of ordinary [[propositional calculi|propositional logic]], from propositional variables, truth-functional connectives, <math>\rightarrow</math>, <math>\wedge</math>, and propositional constant 0. (<math>\lnot \phi</math> is defined as <math>\phi \rightarrow 0</math>) | |
| − | + | Interpretation functions on propositional variables are mappings from the set of propositional variables into [0, 1], and truth functional connectives are interpreted in terms of continuous ''t-norms''. A t-norm <math>\triangle</math> is a binary operator on [0, 1] if <math>\triangle</math> satisfies the following conditions: | |
| − | + | * <math>1 \triangle x=x</math> | |
| − | + | * <math>x\triangle y = y \triangle x</math> | |
| − | + | * <math>x \triangle (y \triangle z) = (x \triangle y) \triangle z</math> | |
| − | + | * if <math>v \leq w</math> and <math>x \leq y</math>, then <math>v \triangle x \leq w \triangle y </math>. | |
| + | A binary connective <math>\triangle</math> is continuous if <math>\triangle</math> satisfies: | ||
| + | : for each <math>\epsilon > 0</math> there is a <math>\delta > 0</math> such that wherever <math>|x_1 -x_2| < \delta</math> and <math>|y_1 - y_2| < \delta</math>, then <math>|(x_1 \triangle y_1) - (x_2 \triangle y_2)| < \epsilon</math>. | ||
| + | Given a t-norm <math>\triangle</math>, the residuum <math>\Rightarrow</math> is defined as: | ||
| + | :<math>x \Rightarrow y </math> = max { ''z''| <math> x \triangle z \leq y </math>} | ||
| + | A t-norm and its residuum interpret <math>\wedge</math> and <math>\Rightarrow</math>, and 0 in [0, 1] interprets the constant 0. Given an interpretation function ''e'' on propositional variables, a t-norm induces a valuation function <math>e_\triangle</math> on every formula. | ||
| + | A formula <math>\phi</math> is called a <math>t-tautology</math> if <math>e_\triangle=1</math>. | ||
| − | + | There is a sound and complete axiomatization, i.e. the system in which a formula <math>\phi</math>is a t-tautology if and only if <math>\phi</math> is provable. | |
| − | + | ===Versions of Fuzzy Propositional Logic=== | |
| + | * _ukasiewicz fuzzy logic is a special case of basic fuzzy logic where conjunction is _ukasiewicz t-norm. It has axioms of basic logic plus additional axiom of double negation (so it is not intuitionistic logic), and its models correspond to MV-algebras. | ||
| + | * Gödel fuzzy logic is a special case of basic fuzzy logic where conjunction is Gödel t-norm. It has axioms of basic logic plus additional axiom of idempotence of conjunction, and its models are called G-algebras. | ||
| + | * Product fuzzy logic is a special case of basic fuzzy logic where conjunction is product t-norm. It has axioms of basic logic plus additional axiom, and its models are called product algebras. | ||
| + | * Rational Pavelka logic is a generalization of multi-valued logic. It is an extension of _ukasziewicz fuzzy logic with additional constants. | ||
| − | + | === Basic Fuzzy Predicate Logic === | |
| − | + | The language of ''basic fuzzy predicate logic'' consists of the same items as the [[first-order logic]] (variables, predicate symbols, <math>\wedge</math>, <math>\rightarrow</math>, 0, quantifiers). An interpretation consists of a nonempty domain and a function that maps an n-ary predicate symbol to an n-ary fuzzy relation (an n-ary fuzzy relation here is a mapping from n-ary tuples of objects in the domain to values in [0, 1]. An n-ary fuzzy relation that corresponds to a predicate symbol ''R'' represents the degrees in which n-ary tuples satisfy the formula <math>Rx_1...x_n</math>. Given a continuous t-norm, the connectives are interpreted as in the case of basic fuzzy propositional logic. The truth degree of a formula of the form <math>\forall x \phi</math> is defined as the infimum of the truth degrees of the instances of <math>\phi</math>, and that of a formula of the form <math>\exists x \phi</math> is defined as the supremum of the instances of <math>\phi</math>. The interpretations of basic fuzzy predicate logic generalize to so-called ''BL-algebra'', and, based on the interpretation, a sound and complete axiomatization can be given (see Hájek 1998 for details). | |
| − | |||
| − | + | == Misconceptions and controversies== | |
| + | ;Fuzzy logic is the same as "imprecise logic." | ||
| + | :Fuzzy logic is not any less precise than any other form of logic: it is an organized and mathematical method of handling ''inherently'' imprecise concepts. The concept of "coldness" cannot be expressed in an equation, because although temperature is a quantity, "coldness" is not. However, people have an idea of what "cold" is, and agree that something cannot be "cold" at N degrees but "not cold" at N+1 degrees—a concept classical logic cannot easily handle due to the principle of bivalence. | ||
| − | + | ;Fuzzy logic is a new way of expressing probability. | |
| + | :Fuzzy logic and probability refer to different kinds of uncertainty. Fuzzy logic is specifically designed to deal with '''imprecision''' of facts (fuzzy logic statements), while probability deals with '''chances''' of that happening ''(but still considering the result to be precise)''. However, this is a point of controversy. Many [[statisticians]] are persuaded by the work of Bruno de Finetti that only one kind of mathematical uncertainty is needed and thus fuzzy logic is unnecessary. On the other hand, Bart Kosko argues that probability is a subtheory of fuzzy logic, as probability only handles one kind of uncertainty. He also claims to have proven a theorem demonstrating that Bayes' theorem can be derived from the concept of fuzzy subsethood. Lotfi Zadeh, the creator of fuzzy logic, argues that fuzzy logic is different in character from probability, and is not a replacement for it. He has created a fuzzy alternative to probability, which he calls [[possibility theory]]. Other controversial approaches to uncertainty include Dempster-Shafer theory and rough sets. | ||
| − | + | ;Fuzzy logic will be difficult to scale to larger problems. | |
| − | + | :In a widely circulated and highly controversial paper in 1993, Charles Elkan commented that "...there are few, if any, published reports of expert systems in real-world use that reason about uncertainty using fuzzy logic. It appears that the limitations of fuzzy logic have not been detrimental in control applications because current fuzzy controllers are far simpler than other knowledge-based systems. In future, the technical limitations of fuzzy logic can be expected to become important in practice, and work on fuzzy controllers will also encounter several problems of scale already known for other knowledge-based systems." Reactions to Elkan's paper are many and varied, from claims that he is simply mistaken, to others who accept that he has identified important limitations of fuzzy logic that need to be addressed by system designers. In fact, fuzzy logic wasn't largely used at that time, and today it is used to solve very complex problems in the [[Artificial intelligence|AI]] area. Probably the scalability and complexity of the ''fuzzy'' system will depend more on its implementation than on the theory of fuzzy logic. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== See also == | == See also == | ||
* [[Artificial intelligence]] | * [[Artificial intelligence]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
* [[Dynamic logic]] | * [[Dynamic logic]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Bibliography == | == Bibliography == | ||
| − | * | + | * von Altrock, Constantin. 2002. ''Fuzzy Logic and NeuroFuzzy Applications Explained''. ISBN 0133684652 |
| − | * | + | * Cox, Earl. 1994. ''The Fuzzy Systems Handbook''. ISBN 0121942708 |
| − | * Charles | + | * Elkan, Charles. ''The Paradoxical Success of Fuzzy Logic''. November 1993. Available from [http://www.cse.ucsd.edu/users/elkan/ Elkan's home page] Retrieved September 18, 2008. |
| − | * Frank | + | * Hájek, Petr. “Metamathematics of fuzzy logic.” Kluwer, 1998. |
| − | * George | + | * Höppner, Frank, Frank Klawonn, Rudolf Kruse and Thomas Runkler. 1999. ''Fuzzy Cluster Analysis''. ISBN 0471988642 |
| − | * George | + | * Klir, George and Tina Folger. 1988. ''Fuzzy Sets, Uncertainty, and Information''. ISBN 0133459845 |
| − | * George | + | * Klir, George, UTE H. St. Clair and Bo Yuan. 1997. ''Fuzzy Set Theory Foundations and Applications''. |
| − | * | + | * Klir, George and Bo Yuan. 1995. ''Fuzzy Sets and Fuzzy Logic''. ISBN 0131011715 |
| − | * Kevin M. | + | * Kosko, Bart. 1993. ''Fuzzy Thinking: The New Science of Fuzzy Logic''. Hyperion. ISBN 078688021X |
| + | * Nguyen, Hung T. 2006. ''A First Course in Fuzzy Logic'', 3rd edition. Boca Raton: Chapman & Hall/CRC. | ||
| + | * Passino, Kevin M. and Stephen Yurkovich. 1998. ''Fuzzy Control''. Menlo Park, CA: Addison Wesley Longman. | ||
| + | * Yager, Ronald and Dimitar Filev. 1994. ''Essentials of Fuzzy Modeling and Control''. ISBN 0471017612 | ||
| + | * Zimmermann, Hans-Jürgen. 2001. ''Fuzzy Set Theory and its Applications''. ISBN 0792374355 | ||
== External links == | == External links == | ||
| + | All links retrieved May 16, 2017. | ||
| + | |||
| + | *[http://udel.edu/~ebenson/Journal_Articles/Benson_ASAE_2000_Adaptive_Edge_Detection.pdf Machine Vision] | ||
*[http://www-2.cs.cmu.edu/Groups/AI/html/faqs/ai/fuzzy/part1/faq.html Fuzzy Logic Newsgroup FAQ] | *[http://www-2.cs.cmu.edu/Groups/AI/html/faqs/ai/fuzzy/part1/faq.html Fuzzy Logic Newsgroup FAQ] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
*[http://plato.stanford.edu/entries/logic-fuzzy/ Stanford Encyclopedia of Philosophy entry] | *[http://plato.stanford.edu/entries/logic-fuzzy/ Stanford Encyclopedia of Philosophy entry] | ||
| − | + | *[http://www.lcc.uma.es/~ppgg/FSQL/ Web page about FSQL] References and links about FSQL. | |
| − | |||
| − | * [http://www.lcc.uma.es/~ppgg/FSQL/ Web page about FSQL] | ||
| − | |||
| − | === | + | ===General Philosophy Sources=== |
| − | *[http:// | + | *[http://plato.stanford.edu/ Stanford Encyclopedia of Philosophy] |
| − | + | *[http://www.iep.utm.edu/ The Internet Encyclopedia of Philosophy] | |
| − | + | *[http://www.bu.edu/wcp/PaidArch.html Paideia Project Online] | |
| − | *[http://www. | + | *[http://www.gutenberg.org/ Project Gutenberg] |
| − | |||
| − | |||
| − | |||
| − | *[http://www. | ||
| − | |||
| − | *[http://www. | ||
| − | [[Category: | + | [[Category:Philosophy]] |
| − | |||
| − | |||
| − | |||
[[Category:Philosophy and religion]] | [[Category:Philosophy and religion]] | ||
| − | {{Credit| | + | {{Credit|65694465}} |
Revision as of 07:38, 23 January 2023
Fuzzy logic, when construed in a wider sense, is the theory of fuzzy sets. The concept of fuzzy sets provides a convenient way to represent various notions with imprecision, vagueness, or fuzziness, for example young, tall, cold, and so forth, which we frequently employ in our everyday life. As such, fuzzy logic has the rationale of more closely resembling than traditional logic the way human beings actually think, where alternatives are not black and white but shades of gray. Fuzzy logic has had notable success in various engineering applications.
When construed in a narrower sense, fuzzy logic is an extension of ordinary two-valued logic in such a way that the points in interval units are allowed as truth-values. As the truth-values are generalized in such a way, usual truth-functional operations are generalized accordingly.
Fuzzy logic is controversial in some circles, despite wide acceptance and a broad track record of successful applications. It is rejected by some control engineers for validation and other reasons, and by some statisticians who hold that probability is the only rigorous mathematical description of uncertainty. Critics also argue that it cannot be a superset of ordinary set theory since membership functions are defined in terms of conventional sets.
Fuzzy Sets
Fuzzy logic studies fuzzy sets, which was first introduced by L. Zadeh in 1965. Zadeh maintains that the meanings of many words in natural language come with degrees. Twelve years old and 18 years old are clearly both young; however 12 years old is younger than 18 years old. To represent this, he introduces the concept of fuzzy subsets. A fuzzy subset of a given set U is a function from U into [1, 0]. The value that a given fuzzy set A assigns to an element x in U is called the degree of the membership of x in the fuzzy set A. Fuzzy subsets are usually referred to simply as fuzzy sets. Using this framework, the meaning of, say, the word “young” can be represented. Take the set of natural numbers and define some fuzzy set, as you like, that assigns values in the unit interval to natural numbers so that, say, 12 (years old) get some value (e.g. .95) higher than the value that 18 (e.g. .85). In that case, the value that each number gets assigned represents the degree of youth. The degree of the membership of 12 in the “youth” subset is higher than that of 18.
This concept of fuzzy sets generalizes the concept of sets in ordinary set theory. Given a set U, a subset S, in the ordinary sense, of U are determined by a function from U to [1, 0]. The elements of U that get 1 assigned represent the elements in S and the elements that get 0 assigned represent the elements that are not in S. The elements of U are all either in, or not in, the subset. However, fuzzy subsets are allowed to take any value in the unit interval other than just 1 and 0. In this sense, the sets in the ordinary sense are special cases of fuzzy sets.
Applications in Engineering
Examples
Fuzzy logic can be used to control household appliances such as washing machines (which sense load size and detergent concentration and adjust their wash cycles accordingly) and refrigerators.
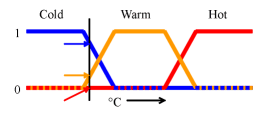
A basic application might characterize subranges of a continuous variable. For instance, a temperature measurement for anti-lock brakes might have several separate membership functions defining particular temperature ranges needed to control the brakes properly. Each function maps the same temperature value to a truth value in the 0 to 1 range. These truth values can then be used to determine how the brakes should be controlled.
In this image, cold, warm, and hot are functions mapping a temperature scale. A point on that scale has three "truth values"—one for each of the three functions. For the particular temperature shown, the three truth values could be interpreted as describing the temperature as, say, "fairly cold," "slightly warm," and "not hot."
A more sophisticated practical example is the use of fuzzy logic in high-performance error correction to improve information reception over a limited-bandwidth communication link affected by data-corrupting noise using turbo codes. The front-end of a decoder produces a likelihood measure for the value intended by the sender (0 or 1) for each bit in the data stream. The likelihood measures might use a scale of 256 values between extremes of "certainly 0" and "certainly 1." Two decoders may analyze the data in parallel, arriving at different likelihood results for the values intended by the sender. Each can then use as additional data the other's likelihood results, and repeats the process to improve the results until consensus is reached as to the most likely values.
Other Examples
- Automobile and other vehicle subsystems, such as ABS and cruise control (e.g. Tokyo monorail)
- Air conditioners
- The MASSIVE engine used in the Lord of the Rings films, which helped show huge scale armies create random, yet orderly movements
- Cameras
- Digital image processing, such as edge detection
- Rice cookers
- Dishwashers
- Elevators
- Washing machines and other home appliances
- Video game artificial intelligence
- Language filters on message boards and chat rooms for filtering out offensive text
- Pattern recognition in Remote Sensing
Fuzzy logic has also been incorporated into some microcontrollers and microprocessors, for instance, the Freescale 68HC12.
Formal Fuzzy Logics
Fuzzy logic, when narrowly construed, is an extension of ordinary logics. The basic idea is that, in fuzzy extensions of logics, formulas can take any values in the unit interval, instead of just 1 or 0 as in ordinary logics.
Basic Fuzzy Propositional Logic
In basic fuzzy propositional logic, formulas are built, as in the language of ordinary propositional logic, from propositional variables, truth-functional connectives, , , and propositional constant 0. ( is defined as )
Interpretation functions on propositional variables are mappings from the set of propositional variables into [0, 1], and truth functional connectives are interpreted in terms of continuous t-norms. A t-norm is a binary operator on [0, 1] if satisfies the following conditions:
- if and , then .
A binary connective is continuous if satisfies:
- for each there is a such that wherever and , then .
Given a t-norm , the residuum is defined as:
- = max { z| }
A t-norm and its residuum interpret and , and 0 in [0, 1] interprets the constant 0. Given an interpretation function e on propositional variables, a t-norm induces a valuation function on every formula. A formula is called a if .
There is a sound and complete axiomatization, i.e. the system in which a formula is a t-tautology if and only if is provable.
Versions of Fuzzy Propositional Logic
- _ukasiewicz fuzzy logic is a special case of basic fuzzy logic where conjunction is _ukasiewicz t-norm. It has axioms of basic logic plus additional axiom of double negation (so it is not intuitionistic logic), and its models correspond to MV-algebras.
- Gödel fuzzy logic is a special case of basic fuzzy logic where conjunction is Gödel t-norm. It has axioms of basic logic plus additional axiom of idempotence of conjunction, and its models are called G-algebras.
- Product fuzzy logic is a special case of basic fuzzy logic where conjunction is product t-norm. It has axioms of basic logic plus additional axiom, and its models are called product algebras.
- Rational Pavelka logic is a generalization of multi-valued logic. It is an extension of _ukasziewicz fuzzy logic with additional constants.
Basic Fuzzy Predicate Logic
The language of basic fuzzy predicate logic consists of the same items as the first-order logic (variables, predicate symbols, , , 0, quantifiers). An interpretation consists of a nonempty domain and a function that maps an n-ary predicate symbol to an n-ary fuzzy relation (an n-ary fuzzy relation here is a mapping from n-ary tuples of objects in the domain to values in [0, 1]. An n-ary fuzzy relation that corresponds to a predicate symbol R represents the degrees in which n-ary tuples satisfy the formula . Given a continuous t-norm, the connectives are interpreted as in the case of basic fuzzy propositional logic. The truth degree of a formula of the form is defined as the infimum of the truth degrees of the instances of , and that of a formula of the form is defined as the supremum of the instances of . The interpretations of basic fuzzy predicate logic generalize to so-called BL-algebra, and, based on the interpretation, a sound and complete axiomatization can be given (see Hájek 1998 for details).
Misconceptions and controversies
- Fuzzy logic is the same as "imprecise logic."
- Fuzzy logic is not any less precise than any other form of logic: it is an organized and mathematical method of handling inherently imprecise concepts. The concept of "coldness" cannot be expressed in an equation, because although temperature is a quantity, "coldness" is not. However, people have an idea of what "cold" is, and agree that something cannot be "cold" at N degrees but "not cold" at N+1 degrees—a concept classical logic cannot easily handle due to the principle of bivalence.
- Fuzzy logic is a new way of expressing probability.
- Fuzzy logic and probability refer to different kinds of uncertainty. Fuzzy logic is specifically designed to deal with imprecision of facts (fuzzy logic statements), while probability deals with chances of that happening (but still considering the result to be precise). However, this is a point of controversy. Many statisticians are persuaded by the work of Bruno de Finetti that only one kind of mathematical uncertainty is needed and thus fuzzy logic is unnecessary. On the other hand, Bart Kosko argues that probability is a subtheory of fuzzy logic, as probability only handles one kind of uncertainty. He also claims to have proven a theorem demonstrating that Bayes' theorem can be derived from the concept of fuzzy subsethood. Lotfi Zadeh, the creator of fuzzy logic, argues that fuzzy logic is different in character from probability, and is not a replacement for it. He has created a fuzzy alternative to probability, which he calls possibility theory. Other controversial approaches to uncertainty include Dempster-Shafer theory and rough sets.
- Fuzzy logic will be difficult to scale to larger problems.
- In a widely circulated and highly controversial paper in 1993, Charles Elkan commented that "...there are few, if any, published reports of expert systems in real-world use that reason about uncertainty using fuzzy logic. It appears that the limitations of fuzzy logic have not been detrimental in control applications because current fuzzy controllers are far simpler than other knowledge-based systems. In future, the technical limitations of fuzzy logic can be expected to become important in practice, and work on fuzzy controllers will also encounter several problems of scale already known for other knowledge-based systems." Reactions to Elkan's paper are many and varied, from claims that he is simply mistaken, to others who accept that he has identified important limitations of fuzzy logic that need to be addressed by system designers. In fact, fuzzy logic wasn't largely used at that time, and today it is used to solve very complex problems in the AI area. Probably the scalability and complexity of the fuzzy system will depend more on its implementation than on the theory of fuzzy logic.
See also
- Artificial intelligence
- Dynamic logic
Bibliography
- von Altrock, Constantin. 2002. Fuzzy Logic and NeuroFuzzy Applications Explained. ISBN 0133684652
- Cox, Earl. 1994. The Fuzzy Systems Handbook. ISBN 0121942708
- Elkan, Charles. The Paradoxical Success of Fuzzy Logic. November 1993. Available from Elkan's home page Retrieved September 18, 2008.
- Hájek, Petr. “Metamathematics of fuzzy logic.” Kluwer, 1998.
- Höppner, Frank, Frank Klawonn, Rudolf Kruse and Thomas Runkler. 1999. Fuzzy Cluster Analysis. ISBN 0471988642
- Klir, George and Tina Folger. 1988. Fuzzy Sets, Uncertainty, and Information. ISBN 0133459845
- Klir, George, UTE H. St. Clair and Bo Yuan. 1997. Fuzzy Set Theory Foundations and Applications.
- Klir, George and Bo Yuan. 1995. Fuzzy Sets and Fuzzy Logic. ISBN 0131011715
- Kosko, Bart. 1993. Fuzzy Thinking: The New Science of Fuzzy Logic. Hyperion. ISBN 078688021X
- Nguyen, Hung T. 2006. A First Course in Fuzzy Logic, 3rd edition. Boca Raton: Chapman & Hall/CRC.
- Passino, Kevin M. and Stephen Yurkovich. 1998. Fuzzy Control. Menlo Park, CA: Addison Wesley Longman.
- Yager, Ronald and Dimitar Filev. 1994. Essentials of Fuzzy Modeling and Control. ISBN 0471017612
- Zimmermann, Hans-Jürgen. 2001. Fuzzy Set Theory and its Applications. ISBN 0792374355
External links
All links retrieved May 16, 2017.
- Machine Vision
- Fuzzy Logic Newsgroup FAQ
- Stanford Encyclopedia of Philosophy entry
- Web page about FSQL References and links about FSQL.
General Philosophy Sources
- Stanford Encyclopedia of Philosophy
- The Internet Encyclopedia of Philosophy
- Paideia Project Online
- Project Gutenberg
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.