Inductance

Electromagnetism
Electricity · Magnetism
Electrostatics Electric charge Coulomb's law Electric field Gauss's law Electric potential Electric dipole moment
Magnetostatics Ampère's circuital law Magnetic field Magnetic flux Biot-Savart law Magnetic dipole moment
Electrodynamics Electric current Lorentz force law Electromotive force (EM) Electromagnetic induction Faraday-Lenz law Displacement current Maxwell's equations (EMF) Electromagnetic field (EM) Electromagnetic radiation
Electrical Network Conduction Resistance Capacitance Inductance Impedance Resonant cavities Waveguides
Tensors in Relativity Electromagnetic tensor Electromagnetic stress-energy tensor

Inductance is a property of an electrical circuit whereby a change in the current flowing through the circuit induces an electromotive force (EMF) that opposes the change in current. In electrical circuits, any electric current ($i$) produces a magnetic field around the current-carrying conductor, generating a total magnetic flux ($\Phi$) acting on the circuit. This magnetic flux tends to act to oppose changes in the flux by generating a voltage (a back EMF) that counters or tends to reduce the rate of change in the current. The ratio of the magnetic flux to the current is called the self-inductance, which is usually simply referred to as the inductance of the circuit.

The property of inductance is particularly noticeable and useful in the form of electrical devices known as inductors. An inductor is often a coil of wire wrapped around a material called the core. When an electric current is passed through the coil, a magnetic field is formed around it, and this field causes the inductor to resist changes in the amount of current passing through it.

Inductors have various practical applications. For instance, when combined with capacitors, they are used as chokes in power supplies and to make tuned circuits for radio reception and broadcasting. Also, inductors are employed in transformers for power grids and as energy storage devices in some switched-mode power supplies.

The property of inductance is tapped when using electrical devices known as inductors, some of which are shown here.

Symbols and units

The term 'inductance' was coined by Oliver Heaviside in February 1886.

It is customary to use the symbol $L$ for inductance, possibly in honor of the physicist Heinrich Lenz.

In honor of Joseph Henry, the unit of inductance has been given the name henry (H):

1 H = 1 weber per ampere (Wb/A).

Inductance is a measure of the amount of EMF generated for a unit change in current. For example, an inductor with an inductance of 1 henry produces an EMF of 1 volt when the current through the inductor changes at the rate of 1 ampere per second.

Definitions

The quantitative definition of the (self-)inductance of a wire loop in SI units (webers per ampere) is

$\displaystyle L={\frac {N\Phi }{i}}$

where $\Phi$ denotes the magnetic flux through the area spanned by the loop, and N is the number of wire turns. The flux linkage $\lambda =N\Phi$ thus is

$\displaystyle N{\Phi }=Li$.

There may, however, be contributions from other circuits. Consider for example two circuits $C_{1}$, $C_{2}$, carrying the currents $i_{1}$, $i_{2}$. The flux linkages of $C_{1}$ and $C_{2}$ are given by

$\displaystyle N_{1}\Phi _{1}=L_{11}i_{1}+L_{12}i_{2},$

$\displaystyle N_{2}\Phi _{2}=L_{21}i_{1}+L_{22}i_{2}.$

According to the above definition, $L_{11}$ and $L_{22}$ are the self-inductances of $C_{1}$ and $C_{2}$, respectively. It can be shown (see below) that the other two coefficients are equal: $L_{12}=L_{21}=M$, where $M$ is called the mutual inductance of the pair of circuits.

The number of turns $N_{1}$ and $N_{2}$ occur somewhat asymmetrically in the definition above. But actually $L_{mn}$ always is proportional to the product $N_{m}N_{n}$, and thus the total currents $N_{m}i_{m}$ contribute to the flux.

Self and mutual inductances also occur in the expression

$\displaystyle W={\frac {1}{2}}\sum _{m,n=1}^{K}L_{m,n}i_{m}i_{n}$

for the energy of the magnetic field generated by $K$ electrical circuits where $i_{n}$ is the current in the nth circuit. This equation is an alternative definition of inductance that also applies when the currents are not confined to thin wires so that it is not immediately clear what area is encompassed by the circuit nor how the magnetic flux through the circuit is to be defined.

The definition $L=N\Phi /i$, in contrast, is more direct and more intuitive. It may be shown that the two definitions are equivalent by equating the time derivative of W and the electric power transferred to the system.

Properties of inductance

Taking the time derivative of both sides of the equation $N\Phi =Li$ yields:

$N{\frac {d\Phi }{dt}}=L{\frac {di}{dt}}+{\frac {dL}{dt}}i\,$

In most physical cases, the inductance is constant with time, and so

$N{\frac {d\Phi }{dt}}=L{\frac {di}{dt}}$

By Faraday's Law of Induction we have:

$N{\frac {d\Phi }{dt}}=-{\mathcal {E}}=v$

where ${\mathcal {E}}$ is the Electromotive force (emf) and $v$ is the induced voltage. Note that the emf is opposite to the induced voltage. Thus:

${\frac {di}{dt}}={\frac {v}{L}}$

or

$i(t)={\frac {1}{L}}\int _{0}^{t}v(\tau )d\tau +i(0)$

These equations together state that, for a steady applied voltage v, the current changes in a linear manner, at a rate proportional to the applied voltage, but inversely proportional to the inductance. Conversely, if the current through the inductor is changing at a constant rate, the induced voltage is constant.

The effect of inductance can be understood using a single loop of wire as an example. If a voltage is suddenly applied between the ends of the loop of wire, the current must change from zero to non-zero. However, a non-zero current induces a magnetic field by Ampère's law. This change in the magnetic field induces an emf that is in the opposite direction of the change in current. The strength of this emf is proportional to the change in current and the inductance. When these opposing forces are in balance, the result is a current that increases linearly with time where the rate of this change is determined by the applied voltage and the inductance.

Multiplying the equation for $di/dt$ above with $Li$ leads to

$Li{\frac {di}{dt}}={\frac {d}{dt}}{\frac {L}{2}}i^{2}=iv$

Since iv is the energy transferred to the system per time it follows that $\left(L/2\right)i^{2}$ is the energy of the magnetic field generated by the current.

Phasor circuit analysis and impedance

Using phasors, the equivalent impedance of an inductance is given by:

$Z_{L}=V/I=jL\omega \,$

where

j is the imaginary unit,

L is the inductance,

$\omega =2\pi f\,$ is the angular frequency,

f is the frequency and

$L\omega \ =X_{L}$ is the inductive reactance.

Induced emf

The flux $\Phi _{i}\ \!$ through the i-th circuit in a set is given by:

$\Phi _{i}=\sum _{j}M_{ij}I_{j}=L_{i}I_{i}+\sum _{j\neq i}M_{ij}I_{j}\,$

so that the induced emf, ${\mathcal {E}}$, of a specific circuit, i, in any given set can be given directly by:

${\mathcal {E}}=-{\frac {d\Phi _{i}}{dt}}=-{\frac {d}{dt}}\left(L_{i}I_{i}+\sum _{j\neq i}M_{ij}I_{j}\right)=-\left({\frac {dL_{i}}{dt}}I_{i}+{\frac {dI_{i}}{dt}}L_{i}\right)-\sum _{j\neq i}\left({\frac {dM_{ij}}{dt}}I_{j}+{\frac {dI_{j}}{dt}}M_{ij}\right).$

Coupled inductors

The circuit diagram representation of mutually inducting inductors. The two vertical lines between the inductors indicate a solid core that the wires of the inductor are wrapped around. "n:m" shows the ratio between the number of windings of the left inductor to windings of the right inductor. This picture also shows the dot convention.

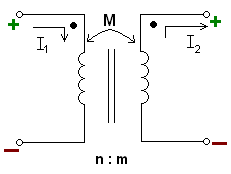
Mutual inductance occurs when the change in current in one inductor induces a voltage in another nearby inductor. It is important as the mechanism by which transformers work, but it can also cause unwanted coupling between conductors in a circuit.

The mutual inductance, M, is also a measure of the coupling between two inductors. The mutual inductance by circuit i on circuit j is given by the double integral Neumann formula, see #Calculation techniques

The mutual inductance also has the relationship:

$M_{21}=N_{1}N_{2}P_{21}\!$

where

$M_{21}$ is the mutual inductance, and the subscript specifies the relationship of the voltage induced in coil 2 to the current in coil 1.

$N_{1}$ is the number of turns in coil 1,

$N_{2}$ is the number of turns in coil 2,

$P_{21}$ is the permeance of the space occupied by the flux.

The mutual inductance also has a relationship with the coupling coefficient. The coupling coefficient is always between 1 and 0, and is a convenient way to specify the relationship between a certain orientation of inductor with arbitrary inductance:

$M=k{\sqrt {L_{1}L_{2}}}\!$

where

k is the coupling coefficient and 0 ≤ k ≤ 1,

$L_{1}$ is the inductance of the first coil, and

$L_{2}$ is the inductance of the second coil.

Once this mutual inductance factor M is determined, it can be used to predict the behavior of a circuit:

$V_{1}=L_{1}{\frac {dI_{1}}{dt}}+M{\frac {dI_{2}}{dt}}$

where

V is the voltage across the inductor of interest,

$L_{1}$ is the inductance of the inductor of interest,

$dI_{1}/dt$ is the derivative, with respect to time, of the current through the inductor of interest,

$M$ is the mutual inductance and

$dI_{2}/dt$ is the derivative, with respect to time, of the current through the inductor that is coupled to the first inductor.

When one inductor is closely coupled to another inductor through mutual inductance, such as in a transformer, the voltages, currents, and number of turns can be related in the following way:

$V_{s}=V_{p}{\frac {N_{s}}{N_{p}}}$

where

$V_{s}$ is the voltage across the secondary inductor,

$V_{p}$ is the voltage across the primary inductor (the one connected to a power source),

$N_{s}$ is the number of turns in the secondary inductor, and

$N_{p}$ is the number of turns in the primary inductor.

Conversely the current:

$I_{s}=I_{p}{\frac {N_{p}}{N_{s}}}$

where

$I_{s}$ is the current through the secondary inductor,

$I_{p}$ is the current through the primary inductor (the one connected to a power source),

$N_{s}$ is the number of turns in the secondary inductor, and

$N_{p}$ is the number of turns in the primary inductor.

Note that the power through one inductor is the same as the power through the other. Also note that these equations don't work if both transformers are forced (with power sources).

When either side of the transformer is a tuned circuit, the amount of mutual inductance between the two windings determines the shape of the frequency response curve. Although no boundaries are defined, this is often referred to as loose-, critical-, and over-coupling. When two tuned circuits are loosely coupled through mutual inductance, the bandwidth will be narrow. As the amount of mutual inductance increases, the bandwidth continues to grow. When the mutual inductance is increased beyond a critical point, the peak in the response curve begins to drop, and the center frequency will be attenuated more strongly than its direct sidebands. This is known as overcoupling.

Calculation techniques

Mutual inductance

The mutual inductance by circuit i on circuit j is given by the double integral Neumann formula

$M_{ij}={\frac {\mu _{0}}{4\pi }}\oint _{C_{i}}\oint _{C_{j}}{\frac {\mathbf {ds} _{i}\cdot \mathbf {ds} _{j}}{|\mathbf {R} _{ij}|}}$

The constant $\mu _{0}$ is the permeability of free space (4$\pi$ × 10^-7 H/m), $C_{i}$ and $C_{j}$ are the curves spanned by the wires, $R_{ij}$ is the distance between two points. See a derivation of this equation.

Self-inductance

Formally the self-inductance of a wire loop would be given by the above equation with i =j. However, $1/R$ now gets singular and the finite radius $a$ and the distribution of the current in the wire must be taken into account. There remain the contribution from the integral over all points where $|R|\geq a/2$ and a correction term,

$L_{jj}=L=\left({\frac {\mu _{0}}{4\pi }}\oint _{C}\oint _{C'}{\frac {\mathbf {ds} \cdot \mathbf {ds} '}{|\mathbf {R} |}}\right)_{|\mathbf {R} |\geq a/2}+{\frac {\mu _{0}}{2\pi }}lY$

Here $a$ and $l$ denote radius and length of the wire, and $Y$ is a constant that depends on the distribution of the current in the wire: $Y=0$ when the current flows in the surface of the wire (skin effect), $Y=1/4$ when the current is homogenuous across the wire. Here is a derivation of this equation.

Method of images

In some cases different current distributions generate the same magnetic field in some section of space. This fact may be used to relate self inductances (method of images). As an example consider:

• A) A wire at distance $d/2$ in front of a perfectly conducting wall (which is the return)
• B) Two parallel wires at distance $d$, with opposite current

The magnetic field of the two systems coincides (in a half space). The magnetic field energy and the inductance of system B thus are twice as large as that of system A.

Self-inductance of simple electrical circuits in air

The self-inductance of many types of electrical circuits can be given in closed form. Examples are listed in the table.

Inductance of simple electrical circuits in air

Type	Inductance / $\mu _{0}$	Comment
Single layer solenoid	${\frac {r^{2}N^{2}}{3l}}\left\{-8w+4{\frac {\sqrt {1+m}}{m}}\left(K\left({\frac {m}{1+m}}\right)-\left(1-m\right)E\left({\frac {m}{1+m}}\right)\right)\right\}$ $={\frac {r^{2}N^{2}\pi }{l}}\left(1-{\frac {8w}{3\pi }}+{\frac {w^{2}}{2}}-{\frac {w^{4}}{4}}+{\frac {5w^{6}}{16}}-{\frac {35w^{8}}{64}}+...\right)$	$N$: Number of turns $r$: Radius $l$: Length $w=r/l$ $m=4w^{2}$ $E,K$: Elliptic integrals
Coaxial cable, high frequency	${\frac {l}{2\pi }}\ln {\frac {a_{1}}{a}}$	a1: Outer radius a: Inner radius $l$: Length
Circular loop	$r\cdot \left(\ln {\frac {8r}{a}}-2+Y\right)$	r: Loop radius a: Wire radius
Rectangle	${\frac {1}{\pi }}\left(b\ln {\frac {2b}{a}}+d\ln {\frac {2d}{a}}-\left(b+d\right)\left(2-Y\right)+2{\sqrt {b^{2}+d^{2}}}-b\cdot \operatorname {arsinh} {\frac {b}{d}}-d\cdot \operatorname {arsinh} {\frac {d}{b}}\right)$	b, d: Border length d >> a, b >> a a: Wire radius
Pair of parallel wires	${\frac {l}{\pi }}\left(\ln {\frac {d}{a}}+Y\right)$	a: Wire radius d: Distance, d ≥ 2a $l$: Length of pair
Pair of parallel wires, high frequency	${\frac {l}{2\pi }}\operatorname {arcosh} \left({\frac {d^{2}}{2a^{2}}}-1\right)$	a: Wire radius d: Distance, d ≥ 2a $l$: Length of pair
Wire parallel to perfectly conducting wall	${\frac {l}{2\pi }}\left(\ln {\frac {2d}{a}}+Y\right)$	a: Wire radius d: Distance, d ≥ a $l$: Length
Wire parallel to conducting wall, high frequency	${\frac {l}{4\pi }}\operatorname {arcosh} \left({\frac {2d^{2}}{a^{2}}}-1\right)$	a: Wire radius d: Distance, d ≥ a $l$: Length

The constant $\mu _{0}$ is the permeability of free space (4$\pi$ × 10^-7 H/m). For high frequencies the electrical current flows in the conductor surface (skin effect), and depending on the geometry it sometimes is necessary to distinguish low and high frequency inductances. This is the purpose of the constant Y: Y=0 when the current is uniformly distributed over the surface of the wire (skin effect), Y=1/4 when the current is uniformly distributed over the cross section of the wire. In the high frequency case, if conductors approach each other, an additional screening current flows in their surface, and expressions containing Y become invalid.

Inductance of a solenoid

A solenoid is a long, thin coil, i.e. a coil whose length is much greater than the diameter. Under these conditions, and without any magnetic material used, the magnetic flux density $B$ within the coil is practically constant and is given by

$\displaystyle B=\mu _{0}Ni/l$

where $\mu _{0}$ is the permeability of free space, $N$ the number of turns, $i$ the current and $l$ the length of the coil. Ignoring end effects the total magnetic flux through the coil is obtained by multiplying the flux density $B$ by the cross-section area $A$ and the number of turns $N$:

$\displaystyle \Phi =\mu _{0}N^{2}iA/l,$

from which it follows that the inductance of a solenoid is given by:

$\displaystyle L=\mu _{0}N^{2}A/l.$

This, and the inductance of more complicated shapes, can be derived from Maxwell's equations. For rigid air-core coils, inductance is a function of coil geometry and number of turns, and is independent of current.

Similar analysis applies to a solenoid with a magnetic core, but only if the length of the coil is much greater than the product of the relative permeability of the magnetic core and the diameter. That limits the simple analysis to low-permeability cores, or extremely long thin solenoids. Although rarely useful, the equations are,

$\displaystyle B=\mu _{0}\mu _{r}Ni/l$

where $\mu _{r}$ the relative permeability of the material within the solenoid,

$\displaystyle \Phi =\mu _{0}\mu _{r}N^{2}iA/l,$

from which it follows that the inductance of a solenoid is given by:

$\displaystyle L=\mu _{0}\mu _{r}N^{2}A/l.$

Note that since the permeability of ferromagnetic materials changes with applied magnetic flux, the inductance of a coil with a ferromagnetic core will generally vary with current.

Inductance of a coaxial line

Let the inner conductor have radius $r_{i}$ and permeability $\mu _{i}$, let the dielectric between the inner and outer conductor have permeability $\mu _{d}$, and let the outer conductor have inner radius $r_{o1}$, outer radius $r_{o2}$, and permeability $\mu _{o}$. Assume that a DC current $I$ flows in opposite directions in the two conductors, with uniform current density. The magnetic field generated by these currents points in the azimuthal direction and is a function of radius $r$; it can be computed using Ampère's Law:

$0\leq r\leq r_{i}:B(r)={\frac {\mu _{i}Ir}{2\pi r_{i}^{2}}}$

$r_{i}\leq r\leq r_{o1}:B(r)={\frac {\mu _{d}I}{2\pi r}}$

$r_{o1}\leq r\leq r_{o2}:B(r)={\frac {\mu _{o}I}{2\pi r}}\left({\frac {r_{o2}^{2}-r^{2}}{r_{o2}^{2}-r_{o1}^{2}}}\right)$

The flux per length $l$ in the region between the conductors can be computed by drawing a surface containing the axis:

${\frac {d\phi _{d}}{dl}}=\int _{r_{i}}^{r_{o1}}B(r)dr={\frac {\mu _{d}I}{2\pi }}\ln {\frac {r_{o1}}{r_{i}}}$

Inside the conductors, L can be computed by equating the energy stored in an inductor, ${\frac {1}{2}}LI^{2}$, with the energy stored in the magnetic field:

${\frac {1}{2}}LI^{2}=\int _{V}{\frac {B^{2}}{2\mu }}dV$

For a cylindrical geometry with no $l$ dependence, the energy per unit length is

${\frac {1}{2}}L'I^{2}=\int _{r_{1}}^{r_{2}}{\frac {B^{2}}{2\mu }}2\pi r~dr$

where $L'$ is the inductance per unit length. For the inner conductor, the integral on the right-hand-side is ${\frac {\mu _{i}I^{2}}{16\pi }}$; for the outer conductor it is ${\frac {\mu _{o}I^{2}}{4\pi }}\left({\frac {r_{o2}^{2}}{r_{o2}^{2}-r_{o1}^{2}}}\right)^{2}\ln {\frac {r_{o2}}{r_{o1}}}-{\frac {\mu _{o}I^{2}}{8\pi }}\left({\frac {r_{o2}^{2}}{r_{o2}^{2}-r_{o1}^{2}}}\right)-{\frac {\mu _{o}I^{2}}{16\pi }}$

Solving for $L'$ and summing the terms for each region together gives a total inductance per unit length of:

$L'={\frac {\mu _{i}}{8\pi }}+{\frac {\mu _{d}}{2\pi }}\ln {\frac {r_{o1}}{r_{i}}}+{\frac {\mu _{o}}{2\pi }}\left({\frac {r_{o2}^{2}}{r_{o2}^{2}-r_{o1}^{2}}}\right)^{2}\ln {\frac {r_{o2}}{r_{o1}}}-{\frac {\mu _{o}}{4\pi }}\left({\frac {r_{o2}^{2}}{r_{o2}^{2}-r_{o1}^{2}}}\right)-{\frac {\mu _{o}}{8\pi }}$

However, for a typical coaxial line application we are interested in passing (non-DC) signals at frequencies for which the resistive skin effect cannot be neglected. In most cases, the inner and outer conductor terms are negligible, in which case one may approximate

${\frac {dL}{dl}}\approx {\frac {\mu _{d}}{2\pi }}\ln {\frac {r_{o1}}{r_{i}}}$

See also

• Electromagnetic induction
• Electricity
• Faraday's law of induction
• Inductor
• Magnetism
• Transformer

References

ISBN links support NWE through referral fees

• Griffiths, David J. 1999. Introduction to Electrodynamics, 3rd ed. Upper Saddle River, NJ: Prentice Hall. ISBN 013805326X.
• Grover, Frederick Warren. 1962. Inductance Calculations, Working Formulas and Tables. New York: Dover. OCLC 299921393.
• Heaviside, Oliver. 1894. Electrical Papers. New York: Macmillan.
• Hughes, Edward, et al. 2002. Electrical & Electronic Technology, 8th ed. Harlow: Prentice Hall. ISBN 058240519X.
• Wangsness, Roald K. 1986. Electromagnetic Fields, 2nd ed. New York: Wiley. ISBN 0471811866.

External links

All links retrieved March 2, 2018.

• Inductance Calculator. The Clemson University Vehicular Electronics Laboratory.

Credits

New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:

• Inductance  ^history

The history of this article since it was imported to New World Encyclopedia:

• History of "Inductance"

Note: Some restrictions may apply to use of individual images which are separately licensed.