Difference between revisions of "Venn diagram" - New World Encyclopedia
MaedaMartha (talk | contribs) |
Rosie Tanabe (talk | contribs) |
||
| (11 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[Image:Venn diagram cmyk.svg|thumb| | + | {{Approved}}{{Images OK}}{{Submitted}}{{Paid}}{{copyedited}} |
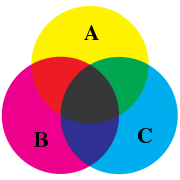
| − | '''Venn diagrams''' are schematic diagrams used in [[logic]] | + | [[Image:Venn diagram cmyk.svg|thumb|180px|right|A Venn diagram of sets A, B, and C]] |
| − | + | '''Venn diagrams''' are schematic diagrams used in [[logic]] and in the branch of mathematics known as [[set theory]] to represent sets and their unions and intersections. They show all of the possible [[mathematics|mathematical]] or logical relationships between sets (groups of things). | |
| − | The [[United Kingdom|British]] [[philosopher]], | + | {{toc}} |
| + | The [[United Kingdom|British]] [[philosopher]], mathematician, and professor of logic, [[John Venn]] (1834–1923), introduced the Venn diagram in his paper, “On the Diagrammatic and Mechanical Representation of Prepositions and Reasonings,” which appeared in the ''Philosophical Magazine and Journal of Science'' in July of 1880. The simplest Venn diagrams consist of two or three intersecting closed curves, but he also gave a construction for Venn diagrams with ''any'' number of curves, where each successive curve is interweaved with previous curves, starting with the three-circle diagram. A. W. F. Edwards, Branko Grünbaum, Charles Lutwidge Dodgson (a.k.a. [[Lewis Carroll]]) developed extended implications of Venn diagrams. Simple Venn diagrams are used in the classroom to teach students logical organization of their thoughts. | ||
==Origins== | ==Origins== | ||
[[Image:Venn-stainedglass-gonville-caius.jpg|thumb|100px|right|Stained glass window in the dining hall of Gonville and Caius College, Cambridge]] | [[Image:Venn-stainedglass-gonville-caius.jpg|thumb|100px|right|Stained glass window in the dining hall of Gonville and Caius College, Cambridge]] | ||
| + | In 1881, Venn further elaborated on his original diagrams in ''Symbolic Logic'' (1881), and continued to improve his method for illustrating propositions by exclusive and inclusive circles. | ||
| − | + | The use of geometrical representations to illustrate syllogistic logic did not originate with Venn; [[Gottfried Leibniz]] used them as well. Venn became critical of the methods used in the nineteenth century diagrams of [[George Boole]] and Augustus de Morgan, and wrote ''Symbolic Logic'' mostly to present his own interpretations and corrections of Boole’s work. Venn's diagrams became the most important part of his work, rather than his attempt to clarify what he believed to be inconsistencies and ambiguities in Boole's logic. | |
| − | |||
| − | The use of geometrical representations to illustrate syllogistic logic did not originate with | ||
A stained glass window representing a Venn diagram in Gonville and Caius College, Cambridge, where Venn studied and spent most of his life, commemorates him. | A stained glass window representing a Venn diagram in Gonville and Caius College, Cambridge, where Venn studied and spent most of his life, commemorates him. | ||
==Venn Diagram== | ==Venn Diagram== | ||
| − | |||
| − | + | A Venn diagram is a schematic diagram used in logic theory to represent sets and their unions and intersections. Venn considered three discs R, S, and T as typical subsets of a set U. The intersections of these discs and their complements divide U into eight non-overlapping regions, the unions of which give 256 different Boolean combinations of the original sets R, S, and T. | |
| − | |||
| − | |||
| − | |||
| − | The region of intersection of the three circles in the order three Venn diagram in the special case of the center of each being located at the intersection of the other two is a geometric shape known as a Reuleaux triangle. | + | The simplest Venn diagram is an order-two diagram consisting of two intersecting circles, producing a total of four regions, A, B, the intersection of A and B, and Ø (the empty set, represented by none of the regions occupied). |
| + | In general, an order Venn diagram is a collection of simple closed curves in the plane such that: | ||
| + | * The curves partition the plane into connected regions, and | ||
| + | * Each subset “S” corresponds to a unique region formed by the intersection of the interiors of the curves in “S.”<ref>Ruskey, F., [http://www.theory.csc.uvic.ca/~cos/inf/comb/SubsetInfo.html#Venn Venn Diagrams.] Retrieved October 25, 2007.</ref> | ||
| + | The region of intersection of the three circles in the order-three Venn diagram, in the special case of the center of each being located at the intersection of the other two, is a geometric shape known as a Reuleaux triangle.<ref>Weisstein, Eric W., [http://mathworld.wolfram.com/VennDiagram.html Venn Diagram.] Retrieved October 25, 2007.</ref> | ||
==Extensions to Higher Numbers of Sets== | ==Extensions to Higher Numbers of Sets== | ||
| − | Venn diagrams typically have three sets. Venn was keen to find | + | |
| + | Venn diagrams typically have three sets. Venn was keen to find “symmetrical figures…elegant in themselves” representing higher numbers of sets, and he devised a four set diagram using [[ellipse]]s. He also gave a construction for Venn diagrams with any number of curves, where each successive curve is interleaved with previous curves, starting with the three-circle diagram. | ||
===Simple Symmetric Venn Diagrams=== | ===Simple Symmetric Venn Diagrams=== | ||
| − | |||
| − | ===Edwards' Venn Diagrams=== | + | In 1963 D.W. Henderson showed that the existence of an ''n''-Venn diagram with ''n''-fold rotational symmetry implied that ''n'' was [[prime number|prime]].<ref> Henderson, D.W., "Venn diagrams for more than four classes," ''American Mathematical Monthly,'' 70, (1963), p. 424–426.</ref> In 2003 work by Griggs, Killian, and Savage showed that this condition is also sufficient.<ref>Ruskey, Frank, Savage, Carla D., and Wagon, Stan, [http://www.ams.org/notices/200611/fea-wagon.pdf The Search for Simple Symmetric Venn Diagrams.] Retrieved October 25, 2007.</ref> |
| + | |||
| + | ===Edwards's Venn Diagrams=== | ||
| + | |||
{| align="right" | {| align="right" | ||
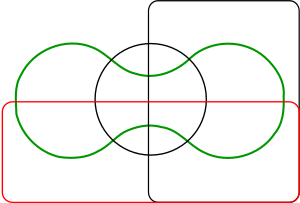
| − | | [[Image:Venn-three.svg|thumb|right|Edwards' Venn diagram of three sets]] | + | | [[Image:Venn-three.svg|thumb|right|Edwards's Venn diagram of three sets]] |
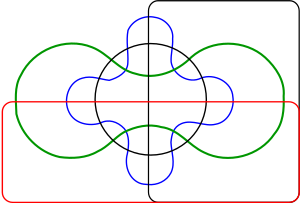
| − | | [[image:Edwards-Venn-four.svg|thumb|right|Edwards' Venn diagram of four sets]] | + | | [[image:Edwards-Venn-four.svg|thumb|right|Edwards's Venn diagram of four sets]] |
|- | |- | ||
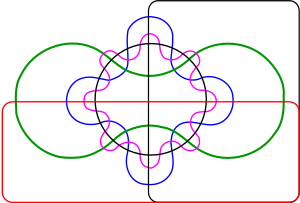
| − | | [[image:Edwards-Venn-five.svg|thumb|right|Edwards' Venn diagram of five sets]] | + | | [[image:Edwards-Venn-five.svg|thumb|right|Edwards's Venn diagram of five sets]] |
| − | | [[Image:Edwards-Venn-six.svg|thumb|right|Edwards' Venn diagram of six sets]] | + | | [[Image:Edwards-Venn-six.svg|thumb|right|Edwards's Venn diagram of six sets]] |
|} | |} | ||
| − | A. W. F. Edwards gave a construction to higher numbers of sets that features some symmetries. His construction is achieved by projecting the Venn diagram onto a [[sphere]]. Three sets can be easily represented by taking three hemispheres at right angles (''x''≥0, ''y''≥0 and ''z''≥0). A fourth set can be represented by taking a curve similar to the seam on a tennis ball which winds up and down around the equator. The resulting sets can then be projected back to the plane to | + | A. W. F. Edwards gave a construction to higher numbers of sets that features some symmetries. His construction is achieved by projecting the Venn diagram onto a [[sphere]]. Three sets can be easily represented by taking three hemispheres at right angles (''x''≥0, ''y''≥0 and ''z''≥0). A fourth set can be represented by taking a curve similar to the seam on a tennis ball which winds up and down around the equator. The resulting sets can then be projected back to the plane to produce “cogwheel” diagrams with increasing numbers of teeth. These diagrams were devised while designing a stained-glass]] window in memoriam to Venn. |
===Other Diagrams=== | ===Other Diagrams=== | ||
| − | Edwards' Venn diagrams are topologically equivalent to diagrams devised by Branko Grünbaum which were based around intersecting polygons with increasing numbers of sides. They are also | + | Edwards's Venn diagrams are topologically equivalent to diagrams devised by Branko Grünbaum which were based around intersecting polygons with increasing numbers of sides. They are also two-dimensional representations of hypercubes. |
Smith devised similar ''n''-set diagrams using sine curves with equations ''y''=sin(2<sup>''i''</sup>''x'')/2<sup>''i''</sup>, 0≤i≤''n''-2. | Smith devised similar ''n''-set diagrams using sine curves with equations ''y''=sin(2<sup>''i''</sup>''x'')/2<sup>''i''</sup>, 0≤i≤''n''-2. | ||
| Line 55: | Line 58: | ||
== Example == | == Example == | ||
| − | |||
| − | |||
| − | + | The orange circle (set ''A'') might represent, for example, all living creatures that are two-legged . The blue circle, (set ''B'') might represent living creatures that can fly. The area where the blue and orange circles overlap (which is called the ''intersection'') contains all living creatures that can fly '''and''' which have two legs—for example, parrots. (Imagine each separate type of creature as a point somewhere in the diagram.) | |
| − | + | Humans and penguins would be in the orange circle, in the part that does not overlap with the blue circle. Mosquitoes have six legs, and fly, so the point for mosquitoes would be in the part of the blue circle that does not overlap with the orange one. Things that do not have two legs and cannot fly (for example, whales and rattlesnakes) would all be represented by points outside both circles. Technically, the Venn diagram above can be interpreted as "the relationships of set ''A'' and set ''B'' that may have some (but not all) elements in common." | |
| − | The area | + | The combined area of sets ''A'' and ''B'' is called the “union” of sets ''A'' and ''B.'' The union in this case contains all things that either have two legs, can fly, or both. |
| − | + | The area in both ''A'' and ''B,'' where the two sets overlap, is defined as ''A''∩''B,'' that is, ''A'' '''intersected''' with ''B.'' The intersection of the two sets is not empty, because the circles overlap, i.e. there are creatures that are in '''both''' the orange and blue circles. | |
| + | Sometimes a rectangle, called the Universal set, is drawn around the Venn diagram to represent the space of all possible things under consideration. As mentioned above, a whale would be represented by a point that is not in the union, but is in the Universe (of living creatures, or of all things, depending on how one chose to define the Universe for a particular diagram). | ||
| + | ==See also== | ||
| + | * [[Boolean algebra]] | ||
==Notes== | ==Notes== | ||
| + | |||
<references/> | <references/> | ||
==References== | ==References== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | *Cieutat, Victor J., Krimerman, Leonard I., and Elder S. Thomas. ''Traditional logic and the Venn diagram; a programed introduction.'' San Francisco: Chandler Pub. Co. 1969. | ||
| + | *Edwards, A. W. F. ''Cogwheels of the mind : the story of Venn diagrams.'' Baltimore: Johns Hopkins University Press. 2004. ISBN 0801874343 | ||
| + | *McCarthy, J.F., and Krishnamoorthy, M.S. "Venn Diagram Construction of Internet Chatroom Conversations." ''Computer Science.'' (3975):535-541. 2006. | ||
| + | *Stewart, Ian. ''Another fine math you've got me into.'' New York: W.H. Freeman. 1992. ISBN 0716723425 | ||
| + | *Venn, John. "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings." ''Dublin Philosophical Magazine and Journal of Science.'' volume 9, 59, 1880. p. 1-18. | ||
| − | === | + | == External Links == |
| − | + | All links retrieved May 3, 2023. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | * Bogomolny, Alexander. [http://www.cut-the-knot.org/LewisCarroll/Venn.shtml Venn Diagrams.] | ||
| + | * Bogomolny, Alexander. [http://www.cut-the-knot.org/LewisCarroll/VennClick.shtml Venn Diagrams (Click).] | ||
| + | * Dunham, William. [http://www.cut-the-knot.org/LewisCarroll/dunham.shtml Lewis Carroll's Logic Game.] | ||
| + | * Rodgers, Peter. [http://www.cs.kent.ac.uk/people/staff/pjr/EulerVennCircles/EulerVennApplet.html Applet for Drawing 3 Set Area-Proportional Venn Diagrams.] | ||
| + | * Ruskey, F., and Weston, M. [http://www.combinatorics.org/Surveys/ds5/VennEJC.html A Survey of Venn Diagrams.] | ||
| + | * SourceForge. [http://sourceforge.net/projects/venn/ Venn Diagrams.] | ||
| − | |||
| − | |||
| − | |||
| + | [[Category:Philosophy and religion]] | ||
| + | [[Category:philosophy]] | ||
| + | [[Category:mathematics]] | ||
{{credit|133208213}} | {{credit|133208213}} | ||
Latest revision as of 17:01, 3 May 2023
Venn diagrams are schematic diagrams used in logic and in the branch of mathematics known as set theory to represent sets and their unions and intersections. They show all of the possible mathematical or logical relationships between sets (groups of things).
The British philosopher, mathematician, and professor of logic, John Venn (1834–1923), introduced the Venn diagram in his paper, “On the Diagrammatic and Mechanical Representation of Prepositions and Reasonings,” which appeared in the Philosophical Magazine and Journal of Science in July of 1880. The simplest Venn diagrams consist of two or three intersecting closed curves, but he also gave a construction for Venn diagrams with any number of curves, where each successive curve is interweaved with previous curves, starting with the three-circle diagram. A. W. F. Edwards, Branko Grünbaum, Charles Lutwidge Dodgson (a.k.a. Lewis Carroll) developed extended implications of Venn diagrams. Simple Venn diagrams are used in the classroom to teach students logical organization of their thoughts.
Origins
In 1881, Venn further elaborated on his original diagrams in Symbolic Logic (1881), and continued to improve his method for illustrating propositions by exclusive and inclusive circles.
The use of geometrical representations to illustrate syllogistic logic did not originate with Venn; Gottfried Leibniz used them as well. Venn became critical of the methods used in the nineteenth century diagrams of George Boole and Augustus de Morgan, and wrote Symbolic Logic mostly to present his own interpretations and corrections of Boole’s work. Venn's diagrams became the most important part of his work, rather than his attempt to clarify what he believed to be inconsistencies and ambiguities in Boole's logic.
A stained glass window representing a Venn diagram in Gonville and Caius College, Cambridge, where Venn studied and spent most of his life, commemorates him.
Venn Diagram
A Venn diagram is a schematic diagram used in logic theory to represent sets and their unions and intersections. Venn considered three discs R, S, and T as typical subsets of a set U. The intersections of these discs and their complements divide U into eight non-overlapping regions, the unions of which give 256 different Boolean combinations of the original sets R, S, and T.
The simplest Venn diagram is an order-two diagram consisting of two intersecting circles, producing a total of four regions, A, B, the intersection of A and B, and Ø (the empty set, represented by none of the regions occupied). In general, an order Venn diagram is a collection of simple closed curves in the plane such that:
- The curves partition the plane into connected regions, and
- Each subset “S” corresponds to a unique region formed by the intersection of the interiors of the curves in “S.”[1]
The region of intersection of the three circles in the order-three Venn diagram, in the special case of the center of each being located at the intersection of the other two, is a geometric shape known as a Reuleaux triangle.[2]
Extensions to Higher Numbers of Sets
Venn diagrams typically have three sets. Venn was keen to find “symmetrical figures…elegant in themselves” representing higher numbers of sets, and he devised a four set diagram using ellipses. He also gave a construction for Venn diagrams with any number of curves, where each successive curve is interleaved with previous curves, starting with the three-circle diagram.
Simple Symmetric Venn Diagrams
In 1963 D.W. Henderson showed that the existence of an n-Venn diagram with n-fold rotational symmetry implied that n was prime.[3] In 2003 work by Griggs, Killian, and Savage showed that this condition is also sufficient.[4]
Edwards's Venn Diagrams
A. W. F. Edwards gave a construction to higher numbers of sets that features some symmetries. His construction is achieved by projecting the Venn diagram onto a sphere. Three sets can be easily represented by taking three hemispheres at right angles (x≥0, y≥0 and z≥0). A fourth set can be represented by taking a curve similar to the seam on a tennis ball which winds up and down around the equator. The resulting sets can then be projected back to the plane to produce “cogwheel” diagrams with increasing numbers of teeth. These diagrams were devised while designing a stained-glass]] window in memoriam to Venn.
Other Diagrams
Edwards's Venn diagrams are topologically equivalent to diagrams devised by Branko Grünbaum which were based around intersecting polygons with increasing numbers of sides. They are also two-dimensional representations of hypercubes.
Smith devised similar n-set diagrams using sine curves with equations y=sin(2ix)/2i, 0≤i≤n-2.
Charles Lutwidge Dodgson (a.k.a. Lewis Carroll) devised a five set diagram.
Classroom Use
Venn diagrams are often used by teachers in the classroom as a graphic organizer, a mechanism to help students compare and contrast two or three “sets” of ideas. Characteristics of each set of ideas are listed in each section of the diagram, with shared characteristics listed in the overlapping sections. Simple Venn diagrams are introduced to students as early as kindergarten, and are used to help students organize their thoughts before writing about them.
In Indian schools the basic Venn diagrams are taught using Indian rupee coins.
Example
The orange circle (set A) might represent, for example, all living creatures that are two-legged . The blue circle, (set B) might represent living creatures that can fly. The area where the blue and orange circles overlap (which is called the intersection) contains all living creatures that can fly and which have two legs—for example, parrots. (Imagine each separate type of creature as a point somewhere in the diagram.)
Humans and penguins would be in the orange circle, in the part that does not overlap with the blue circle. Mosquitoes have six legs, and fly, so the point for mosquitoes would be in the part of the blue circle that does not overlap with the orange one. Things that do not have two legs and cannot fly (for example, whales and rattlesnakes) would all be represented by points outside both circles. Technically, the Venn diagram above can be interpreted as "the relationships of set A and set B that may have some (but not all) elements in common."
The combined area of sets A and B is called the “union” of sets A and B. The union in this case contains all things that either have two legs, can fly, or both.
The area in both A and B, where the two sets overlap, is defined as A∩B, that is, A intersected with B. The intersection of the two sets is not empty, because the circles overlap, i.e. there are creatures that are in both the orange and blue circles.
Sometimes a rectangle, called the Universal set, is drawn around the Venn diagram to represent the space of all possible things under consideration. As mentioned above, a whale would be represented by a point that is not in the union, but is in the Universe (of living creatures, or of all things, depending on how one chose to define the Universe for a particular diagram).
See also
- Boolean algebra
Notes
- ↑ Ruskey, F., Venn Diagrams. Retrieved October 25, 2007.
- ↑ Weisstein, Eric W., Venn Diagram. Retrieved October 25, 2007.
- ↑ Henderson, D.W., "Venn diagrams for more than four classes," American Mathematical Monthly, 70, (1963), p. 424–426.
- ↑ Ruskey, Frank, Savage, Carla D., and Wagon, Stan, The Search for Simple Symmetric Venn Diagrams. Retrieved October 25, 2007.
ReferencesISBN links support NWE through referral fees
- Cieutat, Victor J., Krimerman, Leonard I., and Elder S. Thomas. Traditional logic and the Venn diagram; a programed introduction. San Francisco: Chandler Pub. Co. 1969.
- Edwards, A. W. F. Cogwheels of the mind : the story of Venn diagrams. Baltimore: Johns Hopkins University Press. 2004. ISBN 0801874343
- McCarthy, J.F., and Krishnamoorthy, M.S. "Venn Diagram Construction of Internet Chatroom Conversations." Computer Science. (3975):535-541. 2006.
- Stewart, Ian. Another fine math you've got me into. New York: W.H. Freeman. 1992. ISBN 0716723425
- Venn, John. "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings." Dublin Philosophical Magazine and Journal of Science. volume 9, 59, 1880. p. 1-18.
External Links
All links retrieved May 3, 2023.
- Bogomolny, Alexander. Venn Diagrams.
- Bogomolny, Alexander. Venn Diagrams (Click).
- Dunham, William. Lewis Carroll's Logic Game.
- Rodgers, Peter. Applet for Drawing 3 Set Area-Proportional Venn Diagrams.
- Ruskey, F., and Weston, M. A Survey of Venn Diagrams.
- SourceForge. Venn Diagrams.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.