Dipole
- This article is about the electromagnetic phenomenon.
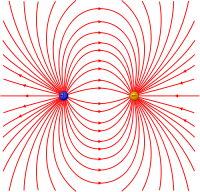
In physics, there are two kinds of dipoles (from the Greek terms di(s)-, meaning "two," and polos, meaning "pivot" or "hinge"): An electric dipole and a magnetic dipole. An electric dipole refers to an object or system in which positive and negative electric charges are located at two separate points. The simplest example is a pair of electric charges of equal magnitude but opposite sign, separated by some small distance. A permanent electric dipole is called an electret.
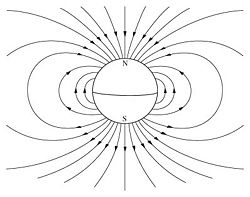
A magnetic dipole is an object or system in which opposite magnetic poles (north and south) are separated by a distance. A magnetic dipole is produced by a closed circuit of electric current.[1] A simple example of this is a single loop of wire with some constant current flowing through it.[2]
Dipole moment
A dipole can be characterized by its dipole moment, a vector quantity. For the simple electric dipole mentioned above, the electric dipole moment points from the negative charge towards the positive charge, and its magnitude is equal to the strength of one of the charges multiplied by the separation between the charges. For a magnetic dipole, the magnetic dipole moment is the strength of either magnetic pole multiplied by the distance separating the two poles. For a magnetic dipole produced by a current loop, its dipole moment points through the loop (according to the right hand grip rule), and its magnitude is equal to the current in the loop times the area of the loop.
In addition to current loops, the electron, among other fundamental particles, is said to have a magnetic dipole moment. This is because it generates a magnetic field which is identical to that generated by a very small current loop. However, to the best of our knowledge, the electron's magnetic moment is not due to a current loop, but is instead an intrinsic property of the electron. It is also possible that the electron has an electric dipole moment, although this has not yet been observed.
A permanent magnet, such as a bar magnet, owes its magnetism to the intrinsic magnetic dipole moment of the electron. The two ends of a bar magnet are referred to as poles (not to be confused with monopoles), and are labeled "north" and "south." The dipole moment of the bar magnet points from its magnetic south to its magnetic north pole. It should be noted that the "north" and "south" convention for magnetic dipoles is the opposite of that used to describe the Earth's geographic and magnetic poles, so that the Earth's geomagnetic north pole is the south pole of its dipole moment. (This should not be difficult to remember; it simply means that the north pole of a bar magnet is the one that points north if used as a compass.)
The only known mechanisms for the creation of magnetic dipoles are by current loops or quantum-mechanical spin since the existence of magnetic monopoles has never been experimentally demonstrated.
Physical dipoles, point dipoles, and approximate dipoles
A physical dipole consists of two equal and opposite point charges: Literally, two poles. Its field at large distances (that is, distances large in comparison to the separation of the poles) depends almost entirely on the dipole moment as defined above. A point (electric) dipole is the limit obtained by letting the separation tend to 0 while keeping the dipole moment fixed. The field of a point dipole has a particularly simple form, and the order-1 term in the multipole expansion is precisely the point dipole field.
Although there are no known magnetic monopoles in nature, there are magnetic dipoles in the form of the quantum-mechanical spin associated with particles such as electrons (although the accurate description of such effects falls outside of classical electromagnetism). A theoretical magnetic point dipole has a magnetic field of the exact same form as the electric field of an electric point dipole. A very small current-carrying loop is approximately a magnetic point dipole; the magnetic dipole moment of such a loop is the product of the current flowing in the loop and the (vector) area of the loop.
Any configuration of charges or currents has a "dipole moment," which describes the dipole whose field is the best approximation, at large distances, to that of the given configuration. This is simply one term in the multipole expansion; when the charge ("monopole moment") is 0—as it always is for the magnetic case, since there are no magnetic monopoles—the dipole term is the dominant one at large distances: its field falls off in proportion to , as compared to for the next (quadrupole) term and higher powers of for higher terms, or for the monopole term.
Molecular dipoles
Many molecules have such dipole moments due to non-uniform distributions of positive and negative charges on their various atoms. For example:
- (positive) H-Cl (negative)
A molecule with a permanent dipole moment is called a polar molecule. A molecule is polarized when it carries an induced dipole. The physical chemist Peter J.W. Debye was the first scientist to study molecular dipoles extensively, and dipole moments are consequently measured in units named debye in his honor.
With respect to molecules there are three types of dipoles:
- Permanent dipoles: These occur when two atoms in a molecule have substantially different electronegativity—one atom attracts electrons more than another becoming more negative, while the other atom becomes more positive. See dipole-dipole attractions.
- Instantaneous dipoles: These occur due to chance when electrons happen to be more concentrated in one place than another in a molecule, creating a temporary dipole. See instantaneous dipole.
- Induced dipoles: These occur when one molecule with a permanent dipole repels another molecule's electrons, "inducing" a dipole moment in that molecule. See induced-dipole attraction.
The definition of an induced dipole given in the previous sentence is too restrictive and misleading. An induced dipole of any polarizable charge distribution (remember that a molecule has a charge distribution) is caused by an electric field external to . This field may, for instance, originate from an ion or polar molecule in the vicinity of or may be macroscopic (for example, a molecule between the plates of a charged capacitor). The size of the induced dipole is equal to the product of the strength of the external field and the dipole polarizability of .
Typical gas phase values of some chemical compounds in debye units:[3]
- Carbon dioxide: 0
- Carbon monoxide: 0.112
- Ozone: 0.53
- Phosgene: 1.17
- Water vapor: 1.85
- Hydrogen cyanide: 2.98
- Cyanamide: 4.27
- Potassium bromide: 10.41
These values can be obtained from measurement of the dielectric constant. When the symmetry of a molecule cancels out a net dipole moment, the value is set at 0. The highest dipole moments are in the range of 10 to 11. From the dipole moment information can be deduced about the molecular geometry of the molecule. For example, the data illustrate that carbon dioxide is a linear molecule but ozone is not.
Field from a magnetic dipole
Magnitude
The far-field strength, B, of a dipole magnetic field is given by
where
- B is the strength of the field, measured in teslas;
- r is the distance from the center, measured in meters;
- λ is the magnetic latitude (90°-θ) where θ = magnetic colatitudes, measured in radians or degrees from the dipole axis (Magnetic colatitudes is 0 along the dipole's axis and 90° in the plane perpendicular to its axis.);
- m is the dipole moment, measured in ampere square-meters (A•m2), which equals joules per tesla;
- μ0 is the permeability of free space, measured in henrys per meter.
Vector form
The field itself is a vector quantity:
where
- B is the field;
- r is the vector from the position of the dipole to the position where the field is being measured;
- r is the absolute value of r: the distance from the dipole;
- is the unit vector parallel to r;
- m is the (vector) dipole moment;
- μ0 is the permeability of free space;
- is the three-dimensional delta function. ( = 0 except at r = (0,0,0), so this term is ignored in multipole expansion.)
This is exactly the field of a point dipole, exactly the dipole term in the multipole expansion of an arbitrary field, and approximately the field of any dipole-like configuration at large distances.
Magnetic vector potential
The vector potential A of a magnetic dipole is
with the same definitions as above.
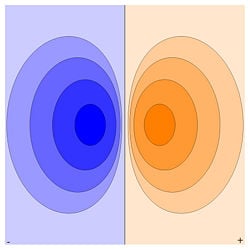
Field from an electric dipole
The electrostatic potential at position due to an electric dipole at the origin is given by:
where
- is a unit vector in the direction of ;
- p is the (vector) dipole moment;
- ε0 is the permittivity of free space.
This term appears as the second term in the multipole expansion of an arbitrary electrostatic potential Φ(r). If the source of Φ(r) is a dipole, as it is assumed here, this term is the only non-vanishing term in the multipole expansion of Φ(r). The electric field from a dipole can be found from the gradient of this potential:
where E is the electric field and is the 3-dimensional delta function. ( = 0 except at r = (0,0,0), so this term is ignored in multipole expansion.) Notice that this is formally identical to the magnetic field of a point magnetic dipole; only a few names have changed.
Torque on a dipole
Since the direction of an electric field is defined as the direction of the force on a positive charge, electric field lines point away from a positive charge and toward a negative charge.
When placed in an electric or magnetic field, equal but opposite forces arise on each side of the dipole creating a torque τ:
for an electric dipole moment p (in coulomb-meters), or
for a magnetic dipole moment m (in ampere-square meters).
The resulting torque will tend to align the dipole with the applied field, which in the case of an electric dipole, yields a potential energy of
- .
The energy of a magnetic dipole is similarly
- .
Quantum mechanical dipole operator
Consider a collection of N particles with charges and position vectors . For instance, this collection may be a molecule consisting of electrons, all with charge -e, and nuclei with charge , where is the atomic number of the i th nucleus. The physical quantity (observable) dipole has the quantum mechanical operator:
Atomic dipoles
A non-degenerate (S-state) atom can have only a zero permanent dipole. This fact follows quantum mechanically from the inversion symmetry of atoms. All 3 components of the dipole operator are antisymmetric under inversion with respect to the nucleus,
where is the dipole operator and is the inversion operator. The permanent dipole moment of an atom in a non-degenerate state (see degenerate energy level) is given as the expectation (average) value of the dipole operator,
where is an S-state, non-degenerate, wavefunction, which is symmetric or antisymmetric under inversion: . Since the product of the wavefunction (in the ket) and its complex conjugate (in the bra) is always symmetric under inversion and its inverse,
it follows that the expectation value changes sign under inversion. We used here the fact that , being a symmetry operator, is unitary: and by definition the Hermitian adjoint may be moved from bra to ket and then becomes . Since the only quantity that is equal to minus itself is the zero, the expectation value vanishes,
In the case of open-shell atoms with degenerate energy levels, one could define a dipole moment by the aid of the first-order Stark effect. This only gives a non-vanishing dipole (by definition proportional to a non-vanishing first-order Stark shift) if some of the wavefunctions belonging to the degenerate energies have opposite parity; that is, have different behavior under inversion. This is a rare occurrence, but happens for the excited H-atom, where 2s and 2p states are "accidentally" degenerate (see this article for the origin of this degeneracy) and have opposite parity (2s is even and 2p is odd).
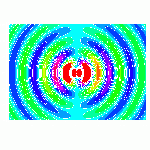
Dipole radiation
In addition to dipoles in electrostatics, it is also common to consider an electric or magnetic dipole that is oscillating in time.
In particular, a harmonically oscillating electric dipole is described by a dipole moment of the form where ω is the angular frequency. In vacuum, this produces fields:
Far away (for ), the fields approach the limiting form of a radiating spherical wave:
which produces a total time-average radiated power P given by
This power is not distributed isotropically, but is rather concentrated around the directions lying perpendicular to the dipole moment. Usually such equations are described by spherical harmonics, but they look very different. A circular polarized dipole is described as a superposition of two linear dipoles.
See also
- Battery (electricity)
- Capacitor
- Electret
- Electric field
- Electric motor
- Electrical conductor
- Electrical engineering
- Electricity
- Electromagnetism
- Electronics
- Electrostatics
- Inductor
- Insulator (electrical)
- Magnetic field
- Magnetism
Notes
- ↑ David J. Griffiths, Introduction to Electrodynamics, 3rd edition (Upper Saddle River, NJ: Prentice Hall, 1999, ISBN 013805326X).
- ↑ Charles A. Brau, Modern Problems in Classical Electrodynamics (Oxford: Oxford University Press, 2004, ISBN 0195146654).
- ↑ Robert C. Weast, CRC Handbook of Chemistry and Physics (Boca Raton, FL: CRC Press., 1984, ISBN 0-8493-0465-2).
ReferencesISBN links support NWE through referral fees
- Bonin, Keith D., and Vitaly V. Kresin. 1997. Electric-Dipole Polarizabilities of Atoms, Molecules and Clusters. River Edge, NJ: World Scientific. ISBN 9810224931.
- Brau, Charles A. 2004. Modern Problems in Classical Electrodynamics. Oxford: Oxford University Press. ISBN 0195146654.
- Demaison, J., H. Hübner, W. Hüttner, and J. Vogt. 2002. Dipole Moments, Quadrupole Coupling Constants, Hindered Rotation and Magnetic Interaction Constants of Diamagnetic Molecules. Berlin: Springer. ISBN 3540410376.
- Gibilisco, Stan. 2005. Electricity Demystified. New York: McGraw-Hill. ISBN 0071439250.
- Griffiths, David J. 1999. Introduction to Electrodynamics, 3rd edition. Upper Saddle River, NJ: Prentice Hall. ISBN 013805326X.
- Young, Hugh D., and Roger A. Freedman. 2003. Physics for Scientists and Engineers, 11th edition. San Francisco: Pearson. ISBN 080538684X.
External links
- USGS Geomagnetism Program. Retrieved June 19, 2008.
- Fields of Force: a chapter from an online textbook. Retrieved June 19, 2008.
- Electric Dipole Potential by Stephen Wolfram and Energy Density of a Magnetic Dipole by Franz Krafft. The Wolfram Demonstrations Project. Retrieved June 19, 2008.
Credits
New World Encyclopedia writers and editors rewrote and completed the Wikipedia article in accordance with New World Encyclopedia standards. This article abides by terms of the Creative Commons CC-by-sa 3.0 License (CC-by-sa), which may be used and disseminated with proper attribution. Credit is due under the terms of this license that can reference both the New World Encyclopedia contributors and the selfless volunteer contributors of the Wikimedia Foundation. To cite this article click here for a list of acceptable citing formats.The history of earlier contributions by wikipedians is accessible to researchers here:
The history of this article since it was imported to New World Encyclopedia:
Note: Some restrictions may apply to use of individual images which are separately licensed.





































![{\displaystyle \mathbf {E} ={\frac {1}{4\pi \varepsilon _{0}}}\left\{{\frac {\omega ^{2}}{c^{2}r}}{\hat {\mathbf {r} }}\times \mathbf {p} \times {\hat {\mathbf {r} }}+\left({\frac {1}{r^{3}}}-{\frac {i\omega }{cr^{2}}}\right)\left[3{\hat {\mathbf {r} }}({\hat {\mathbf {r} }}\cdot \mathbf {p} )-\mathbf {p} \right]\right\}e^{i\omega r/c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0ad1f0c20dbaee5c2469392d307662cf2726f5d)




